80 câu trắc nghiệm Vectơ cơ bản (P1)
-
2022 lượt thi
-
20 câu hỏi
-
20 phút
Danh sách câu hỏi
Câu 1:
19/07/2024Cho tam giác ABC. Hỏi có bao nhiêu vecto khác vecto không có điểm đầu; điểm cuối là các đỉnh của tam giác?
Xem đáp án
Chọn C.
Các vectơ thỏa mãn đầu bài là: 
Câu 2:
21/07/2024Cho tứ giác ABCD. Có bao nhiêu vectơ khác vectơ không có điểm đầu và cuối là các đỉnh của tứ giác?
Xem đáp án
Chọn D.
Một vectơ khác vectơ không được xác định bởi 2 điểm phân biệt.
Từ 4 điểm ban đầu ta có 4 cách chọn điểm đầu và 3 cách chọn điểm cuối.
Do đó; có tất cả 4.3= 12 vecto được tạo ra.
Câu 3:
18/07/2024Cho lục giác đều ABCDEF tâm O . Hỏi có bao nhiêu vecto khác vecto không; cùng phương với có điểm đầu và điểm cuối là các đỉnh của lục giác?
Xem đáp án
Chọn C.
Các vecto cùng phương với 
có điểm đầu và điểm cuối là các đỉnh của lục giác : ,
Vậy có 9 vecto cùng phương với .
Câu 4:
12/07/2024Cho 3 điểm phân biệt A; B; C phân biệt. Khẳng định nào sau đây đúng?
Xem đáp án
Chọn B.
Xét các đáp án:
+ Đáp án A. Ta có 
(dùng quy tắc hình bình hành; với D là điểm thỏa mãn ABCD là hình bình hành). Vậy A sai.
+ Đáp án B. Ta có 
. Vậy B đúng.
+ Đáp án C. Ta có 
(với D là điểm thỏa mãn ABCD là hình bình hành). Vậy C sai.
+ Đáp án D. Ta có 
. Vậy D sai.
Câu 5:
19/07/2024Cho ba điểm phân biệt A; B; C. Đẳng thức nào sau đây đúng?
Xem đáp án
Chọn C.
Xét các đáp án:
+ Đáp án A. Ta có 
. Vậy A sai.
+ Đáp án B. Ta có 
(với D là điểm thỏa mãn ABCD là hình bình hành). Vậy B sai.
+ Đáp án D. ta có: 
. Vậy D sai
Do đó đáp án C đúng.
Câu 6:
23/07/2024Cho ba điểm phân biệt A; B; C. Đẳng thức nào sau đây đúng?
Xem đáp án
Xét các đáp án:
+) Đáp án A. Ta có: . Vậy A sai.
+) Đáp án B. Ta có: (với D là điểm thỏa mãn ABDC là hình bình hành)
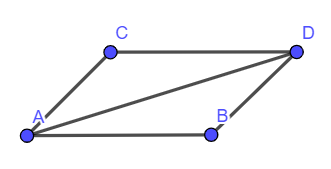
+) Đáp án C. Ta có: . Vậy C đúng.
+) Đáp án D. Ta có: (ABCD là hình bình hành). Do đó D sai.
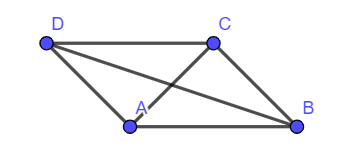
Chọn C
Câu 7:
14/07/2024Cho .Khẳng định nào sau đây đúng?
Xem đáp án
Chọn B.
Ta có 
Do đó:
+ 
ngược hướng.
+ cùng độ dài.
+ ABCD là hình bình hành nếu không cùng giá.
Câu 8:
21/07/2024Cho tam giác ABC cân ở A, đường cao AH. Khẳng định nào sau đây sai?
Xem đáp án
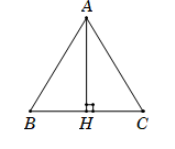
Vì tam giác ABC cân tại A có AH là đường cao nên AH cũng là đường trung tuyến. Do đó H là trung điểm của BC.
và . Do đó B và D đúng.
Ta có: AB = AC ⇒ . Do đó C đúng, A sai.
Chọn A.
Câu 9:
23/07/2024Cho hình vuông ABCD. Khẳng định nào sau đây đúng?
Xem đáp án
Chọn D.
Do ABCD là hình vuông nên :
và 
Câu 10:
19/07/2024Mệnh đề nào sau đây sai?
Xem đáp án
Chọn D.
Với ba điểm phân biệt A; B; C cùng nằm trên một đường thẳng, 
khi và chỉ khi B nằm giữa A và C. Do đó D sai.
Câu 11:
07/10/2024Gọi O là tâm hình vuông ABCD. Tính
Xem đáp án
Đáp án đúng: B.
*Phương pháp giải:
- Nắm kỹ lý thuyết về vectơ và dạng bài tính tổng hiệu hai vecto
*Lời giải:
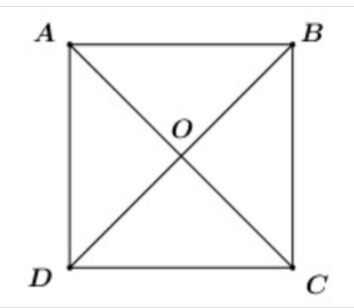
Ta có 
*Một số dạng bài về tích của vectơ với một số
*Lý thuyết cần nắm:
- Tích của vectơ với một số: Cho số k0 và vectơ . Tích của vectơ với số k là một vectơ, kí hiệu là , cùng hướng với nếu k > 0, ngược lại, ngược hướng với nếu k < 0 và có độ dài bằng .
- Tính chất: Với hai vectơ và bất kì, với mọi số h và k, ta có:
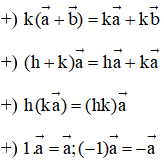
- Quy tắc trung điểm: Nếu I là trung điểm của đoạn thẳng AB thì với mọi điểm M ta có:
- Quy tắc trọng tâm: Nếu G là trọng tâm của tam giác ABC thì với mọi điểm M ta có:
Dạng 1: Tính độ dài vectơ khi biết tích vectơ với một số.
* Phương pháp giải: Sử dụng định nghĩa tích của vectơ với một số, các quy tắc về tổng, hiệu của các vectơ và các hệ thức lượng, định lý Py-ta-go để tính độ dài vectơ đó.
Dạng 2: Tìm một điểm thỏa mãn một đẳng thức vectơ cho trước.
* Phương pháp giải: Biến đổi đẳng thức đã cho về dạng trong đó A là một điểm cố định, cố định và dựng điểm M là điểm thỏa mãn .
Xem thêm các bài viết liên quan hay, chi tiết
Chuyên đề Vectơ lớp 10 (có đáp án)
Trắc nghiệm Tổng hiệu của hai vecto có đáp án – Toán lớp 10
Trắc nghiệm Tích của vecto với một số có đáp án – Toán lớp 10
Câu 12:
18/07/2024Cho tam giác ABC đều cạnh a. Mệnh đề nào sau đây đúng?
Xem đáp án
Chọn C.
Độ dài các cạnh của tam giác là a thì độ dài các vectơ
Câu 13:
19/07/2024Cho tam giác ABC, với M là trung điểm BC. Mệnh đề nào sau đây đúng?
Xem đáp án
Chọn A.
Xét các đáp án:
+ Đáp án A. Ta có (theo quy tắc ba điểm). Do đó đáp án A đúng
+ Đáp án B, C. Ta có (với điểm N là trung điểm của AB). Do đó B, C sai
+ Đáp án D. Ta có . Do đó đáp án D sai.
Câu 14:
19/07/2024Cho tam giác ABC, với M; N ; P lần lượt là trung điểm của BC; CA; AB. Khẳng định nào sau đây sai?
Xem đáp án
+) Đáp án A: Ta có:
Do đó A đúng.
+) Đáp án B: Ta có:
Do đó B đúng.
+) Đáp án C: Ta có:
Do đó C đúng.
+) Đáp án D: Ta có: . Do đó D sai.
Chọn D
Câu 15:
22/07/2024Cho tam giác ABC cân tại A và đường cao AH. Đẳng thức nào sau đây đúng?
Xem đáp án
Chọn C.
Do tam giác cân tại A, AH là đường cao nên H là trung điểm BC.
Xét các đáp án:
+ Đáp án A. Ta có 
+ Đáp án B. Ta có 
+ Đáp án C. Ta có 
( H là trung điểm BC).
+ Đáp án D. Do 
không cùng hướng nên 
.
Câu 16:
12/07/2024Cho M; N; P lần lượt là trung điểm các cạnh AB; BC; CA của tam giác ABC Hỏi vectơ bằng vectơ nào?
Xem đáp án
Chọn B.
Do 
nên 
Câu 17:
13/07/2024Cho đường tròn tâm O và hai tiếp tuyến song song với nhau tiếp xúc với đường tròn tại hai điểm A và B. Mệnh đề nào sau đây đúng?
Xem đáp án
Chọn A.
Do hai tiếp tuyến song song và A; B là hai tiếp điểm nên AB là đường kính.
Do đó ; O là trung điểm của AB. Suy ra 
.
Câu 18:
12/07/2024Cho đường tròn tâm O và hai tiếp tuyến MT và MT’ (T và T’ là hai tiếp điểm). Khẳng định nào sau đây đúng?
Xem đáp án
Chọn C.
Do MT và MT’ là hai tiếp tuyến ( T và T’ là hai tiếp điểm) nên MT = MT’.
Câu 19:
17/07/2024Cho bốn điểm bất kì A; B; C; D. Mệnh đề nào sau đây đúng?
Xem đáp án
Chọn A.
Ta có 
Câu 20:
14/07/2024Cho lục giác đều ABCDEF và O là tâm của nó. Đẳng thức nào sau đây sai?
Xem đáp án
Chọn D.
Ta có OABC là hình bình hành.
( O là trung điểm của BE). Do đó A đúng
Ta có: ( ABCO là hình bình hành)
(FODE là hình bình hành)
Suy ra . Do đó B đúng
Ta có OABC là hình bình hành
. Do đó C đúng