25 câu hỏi trắc nghiệm thuộc Trắc nghiệm Toán 10 Hình học Ôn tập chương 2

Câu 1:

23/07/2024

A (4; 6)

,

B (1; 4)

,

C (7; \frac{3}{2})

. Khẳng định nào sau đây sai

A. $\vec{A B} = (- 3; - 2)$ , $\vec{A C} = (3; - \frac{9}{2})$

B. $\vec{A B} . \vec{A C} = 0$ .

C. $|\vec{A B}| = \sqrt{13}$ .

D. $|\vec{B C}| = \frac{\sqrt{13}}{2}$ .

Xem đáp án

Đáp án: D

Giải thích:

Lời giải

Phương án A: $\vec{A B} = (- 3; - 2)$ , nên loại A.

Phương án B: $\vec{A B} . \vec{A C} = 0$ nên loại B.

Phương án C : $|\vec{A B}| = \sqrt{13}$ nên loại C $\vec{A C} = (3; - \frac{9}{2})$ .

Phương án D: Ta có $\vec{B C} = (6; - \frac{5}{2})$

suy ra $B C = \sqrt[]{6^{2} + {(\frac{5}{2})}^{2}} = \frac{13}{2}$ nên chọn D.

Câu 2:

23/07/2024

Cho biết

\cos α = - \frac{2}{3}

. Tính giá trị của biểu thức

E = \frac{\cot α + 3 \tan α}{2 \cot α + \tan α}

?

A. $- \frac{19}{13}$ .

B. $\frac{19}{13}$ .

C. $\frac{25}{13}$ .

D. $- \frac{25}{13}$

Xem đáp án

Đáp án: B

Giải thích:

Lời giải

$E = \frac{\cot α + 3 \tan α}{2 \cot α + \tan α} = \frac{1 + 3 \tan^{2} α}{2 + \tan^{2} α} = \frac{3 (\tan^{2} α + 1) - 2}{1 + (1 + \tan^{2} α)}$

$= \frac{\frac{3}{\cos^{2} α} - 2}{\frac{1}{\cos^{2} α} + 1} = \frac{3 - 2 \cos^{2} α}{1 + \cos^{2} α} = \frac{19}{13}$

Câu 3:

12/07/2024

Cho biết

\cot α = 5

. Tính giá trị của

E = 2 \cos^{2} α + 5 \sin α \cos α + 1

?

A. $\frac{10}{26}$

B. $\frac{100}{26}$

C. $\frac{50}{26}$

D. $\frac{101}{26}$

Xem đáp án

Đáp án: D

Giải thích:

Lời giải

$E = \sin^{2} α (2 \cot^{2} α + 5 \cot α + \frac{1}{\sin^{2} α}) = \frac{1}{1 + \cot^{2} α} (3 \cot^{2} α + 5 \cot α + 1) = \frac{101}{26}$

Câu 4:

23/07/2024

Trong mặt phẳng Oxy, cho

\vec{a} = (2; - 1)

và

\vec{b} = (- 3; 4)

. Khẳng định nào sau đây là sai?

A. Tích vô hướng của hai vectơ đã cho là -10.

B. Độ lớn của vectơ

\vec{a}

là

\sqrt{5}

.

C. Độ lớn của vectơ $\vec{b}$ là 5.

D. Góc giữa hai vectơ là

90^{o}

.

Xem đáp án

Đáp án: D

Giải thích:

Lời giải

Ta có:

$|\vec{a}| = \sqrt{2^{2} + {(- 1)}^{2}} = \sqrt{5}$

nên B đúng.

$|\vec{b}| = \sqrt{{(- 3)}^{2} + 4^{2}} = 5$ nên C đúng.

$\vec{a} . \vec{b} = 2. (- 3) + (- 1) .4 = - 10 \neq 0$

nên A đúng, D sai.

Câu 5:

23/07/2024

Cho M là trung điểm AB, tìm biểu thức sai:

A. $\vec{M A} . \vec{A B} = - M A . A B$ .

B. $\vec{M A} . \vec{M B} = - M A . M B$ .

C. $\vec{A M} . \vec{A B} = A M . A B$ .

D. $\vec{M A} . \vec{M B} = M A . M B$ .

Xem đáp án

Đáp án: D

Giải thích:

Lời giải

Phương án A: $\vec{M A}, \vec{A B}$ ngược hướng

suy ra

$\vec{M A} . \vec{A B} = M A . A B . \cos 180^{o}$

$= - M A . A B$ nên loại A.

Phương án B: $\vec{M A}, \vec{M B}$ ngược hướng

suy ra

$\vec{M A} . \vec{M B} = M A . M B . \cos 180^{o}$

$= - M A . M B$ nên loại B.

Phương án C: $\vec{A M}, \vec{A B}$ cùng hướng

suy ra

$\vec{A M} . \vec{A B} = A M . A B . \cos 0^{o}$

$= A M . A B$ nên loại C.

Phương án D: $\vec{M A}, \vec{M B}$ ngược hướng

suy ra

$\vec{M A} . \vec{M B} = M A . M B . \cos 180^{o}$

$= - M A . M B$ nên chọn D.

Câu 6:

20/07/2024

Cho tam giác đều ABC cạnh bằng a và H là trung điểm BC. Tính

\vec{A H} . \vec{C A}

A. $\frac{3 a^{2}}{4}$ .

B. $\frac{- 3 a^{2}}{4}$ .

C. $\frac{3 a^{2}}{2}$ .

D. $\frac{- 3 a^{2}}{2}$ .

Xem đáp án

Đáp án: B

Giải thích:

Lời giải

Ta có

$\vec{A H} . \vec{C A} = A H . C A . \cos (\vec{A H}, \vec{C A}) = \frac{a \sqrt{3}}{2} . a . \cos 150^{o} = - \frac{3 a^{2}}{4}$

Câu 7:

21/07/2024

Cho

\vec{a}

và

\vec{b}

là hai vectơ cùng hướng và đều khác vectơ

\vec{0}

. Trong các kết quả sau đây, hãy chọn kết quả đúng:

A. $\vec{a} . \vec{b} = |\vec{a}| . |\vec{b}|$ .

B. $\vec{a} . \vec{b} = 0$ .

C. $\vec{a} . \vec{b} = - 1$ .

D. $\vec{a} . \vec{b} = - |\vec{a}| . |\vec{b}|$ .

Xem đáp án

Đáp án: A

Giải thích:

Lời giải

Ta thấy vế trái của 4 phương án giống nhau.

Bài toán cho $\vec{a}$ và $\vec{b}$ là hai vectơ cùng hướng và đều khác vectơ $\vec{0}$ suy ra $(\vec{a}, \vec{b}) = 0^{0}$

Do đó

$\vec{a} . \vec{b} = |\vec{a}| . |\vec{b}| . \cos 0^{o} = |\vec{a}| . |\vec{b}|$

nên chọn A

Câu 8:

18/07/2024

Cho hình vuông ABCD tâm O. Hỏi mệnh đề nào sau đây sai?

A. $\vec{O A} . \vec{O B} = 0$ .

B. $\vec{O A} . \vec{O C} = \frac{1}{2} \vec{O A} . \vec{A C}$ .

C. $\vec{A B} . \vec{A C} = \vec{A B} . \vec{C D}$ .

D. $\vec{A B} . \vec{A C} = \vec{A C} . \vec{A D}$ .

Xem đáp án

Đáp án: C

Giải thích:

Lời giải

Phương án A: $\vec{O A} ⊥ \vec{O B}$ suy ra $\vec{O A} . \vec{O B} = 0$ nên loại A.

Phương án B:

$\vec{O A} . \vec{O C} = 0$ và $\frac{1}{2} \vec{O A} . \vec{A C} = 0$

$\vec{O A} . \vec{O C} = \frac{1}{2} \vec{O A} . \vec{A C} = 0$ suy ra nên loại B.

Phương án C:

$\vec{A B} . \vec{A C} = A B . A C . \cos 45^{o} = A B . A B \sqrt{2} . \frac{\sqrt{2}}{2} = A B^{2}$

nên chọn C.

Câu 9:

11/07/2024

Trong mặt phẳng Oxy cho

A (- 1; - 1), B (3; 1), C (6; 0)

. Khẳng định nào sau đây đúng.

A. $\vec{A B} = (- 4; - 2)$ , $\vec{A C} = (1; 7)$ .

B. $\hat{B} = 135^{o}$ .

C. $|\vec{A B}| = 20$ .

D. $|\vec{B C}| = 3$ .

Xem đáp án

Đáp án: B

Giải thích:

Lời giải

Phương án A: $\vec{A B} = (4; 2)$ do nên loại A

Phương án B:

Ta có $\vec{A B} = (4; 2)$

suy ra $|\vec{A B}| = \sqrt{20}$ , $\vec{B A} = (- 4; - 2)$

$\vec{B C} = (3; - 1) \Rightarrow B C = \sqrt{10}$

$\cos B = \frac{\vec{B A} . \vec{B C}}{B A . B C} = \frac{- 10}{\sqrt{20} . \sqrt{10}} = \frac{- 1}{\sqrt{2}} \Rightarrow \hat{B} = 135^{o}$

nên chọn B.

Câu 10:

20/07/2024

Cho các vectơ

\vec{a} = (1; - 2), \vec{b} = (- 2; - 6)

. Khi đó góc giữa chúng là

A. $45^{o}$ .

B. $60^{o}$ .

C. $30^{o}$ .

D. $135^{o}$ .

Xem đáp án

Đáp án: A

Giải thích:

Lời giải

Ta có

$\vec{a} = (1; - 2), \vec{b} = (- 2; - 6)$ ,

suy ra :

$\cos (\vec{a}; \vec{b}) = \frac{\vec{a} . \vec{b}}{|\vec{a}| . |\vec{b}|} = \frac{10}{\sqrt{5} . \sqrt{40}} = \frac{\sqrt{2}}{2}$

$\Rightarrow (\vec{a}; \vec{b}) = 45^{o}$

Câu 11:

18/10/2024

Tam giác ABC có

a = 6, b = 4 \sqrt{2}, c = 2.

M là điểm trên cạnh BC sao cho BM=3 . Độ dài đoạn AM bằng bao nhiêu ?

A. $\sqrt{9} .$

B. 9

C. 3

D. $\frac{1}{2} \sqrt{108} .$

Xem đáp án

Đáp án đúng: C

*Phương pháp giải:

- Áp dụng công thức độ dài đường trung tuyến AM trong tam giác ABC để tính ra AM

*Lời giải:

Ta có: Trong tam giác ABC có

$a = 6 \Rightarrow B C = 6$ mà BM=3 suy ra M là trung điểm BC.

Suy ra:

$A M^{2} = m_{a}^{2} = \frac{b^{2} + c^{2}}{2} - \frac{a^{2}}{4} = 9 \Rightarrow A M = 3$

* Các lý thuyết cần nắm về các công thức trong hệ thức lượng tam giác:

Định lí côsin

Cho tam giác ABC có BC = a, AC = b và AB = c. Ta có

a² = b² + c² – 2bc.cosA;

b² = c² + a² – 2ca.cosB;

c² = a² + b² – 2ab.cosC.

Hệ quả

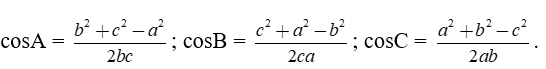
Toán lớp 10 | Chuyên đề: Lý thuyết và Bài tập Toán 10 có đáp án

Định lí sin

Cho tam giác ABC có BC = a, AC = b, AB = c và R là bán kính đường tròn ngoại tiếp.

Ta có

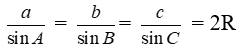
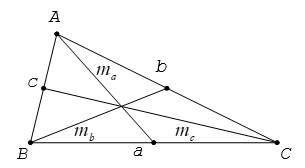
Toán lớp 10 | Chuyên đề: Lý thuyết và Bài tập Toán 10 có đáp án

Độ dài đường trung tuyến

Cho tam giác ABC có ma, mb, mc lần lượt là các trung tuyến kẻ từ A, B, C.

Ta có

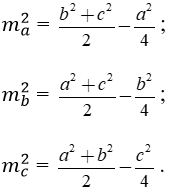
Xem thêm các bài viết liên quan hay, chi tiết:

Lý thuyết Hệ thức lượng trong tam giác – Toán 10 Kết nối tri thức

Giải Toán 10 Bài 6 (Kết nối tri thức): Hệ thức lượng trong tam giác

Sách bài tập Toán 10 Bài 6 (Kết nối tri thức): Hệ thức lượng trong tam giác

Câu 12:

23/07/2024

Cho $Δ A B C$ , biết $\vec{a} = \vec{A B} = (a_{1}; a_{2})$ và $\vec{b} = \vec{A C} = (b_{1}; b_{2})$ . Để tính diện tích S của $Δ A B C$ . Một học sinh làm như sau:

(I)Tính $\cos A = \frac{\vec{a} . \vec{b}}{|\vec{a}| . |\vec{b}|}$

(II)Tính $\sin A = \sqrt{1 - c {os}^{2} A}$

$= \sqrt{1 - \frac{{(\vec{a} . \vec{b})}^{2}}{({|\vec{a}|}^{2} . {|\vec{b}|}^{2})}}$

(III) $S = \frac{1}{2} A B . A C . s i n A$

$= \frac{1}{2} \sqrt{{|\vec{a}|}^{2} {|\vec{b}|}^{2} - {(\vec{a} . \vec{b})}^{2}}$

(IV) $S = \frac{1}{2} \sqrt{(a_{1}^{2} + a_{2}^{2}) (b_{1}^{2} + b_{2}^{2}) - {(a_{1} b_{1} + a_{2} b_{2})}^{2}}$

$S = \frac{1}{2} \sqrt{{(a_{1} b_{2} + a_{2} b_{1})}^{2}}$

$S = \frac{1}{2} (a_{1} b_{2} - a_{2} b_{1})$

Học sinh đó đã làm sai bắt đàu từ bước nào?

A. (I)

B. (II)

C. (III)

D. (IV)

Xem đáp án

Đáp án: A

Giải thích:

Lời giải

Ta có: $\cos A = \frac{|\vec{a} . \vec{b}|}{|\vec{a}| . |\vec{b}|}$

Câu 13:

23/07/2024

Câu nào sau đây là phương tích của điểm M(1;2) đối với đường tròn (C). tâm I(-2;1), bán kính R=2:

A. 6

B. 8

C. 0

D. -5

Xem đáp án

Đáp án: A

Giải thích:

Lời giải

Ta có:

$\vec{M I} = (- 3; 1) \Rightarrow M I = \sqrt{10}$

Phương tích của điểm M đối với đường tròn (C) tâm I là:

$M I^{2} - R^{2} = {(\sqrt{{(- 2 - 1)}^{2} + {(1 - 2)}^{2}})}^{2} - 4 = 6.$

Câu 14:

15/07/2024

Khoảng cách từ A đến B không thể đo trực tiếp được vì phải qua một đầm lầy. Người ta xác định được một điểm C mà từ đó có thể nhìn được A và B dưới một góc

78^{o} 24'

. Biết

C A = 250 m, C B = 120 m

. Khoảng cách AB bằng bao nhiêu ?

A. 266m

B. 255m

C. 166m

D. 298m

Xem đáp án

Đáp án: B

Giải thích:

Lời giải

Ta có:

$A B^{2} = C A^{2} + C B^{2} - 2 C B . C A . \cos C = 250^{2} + 120^{2} - 2.250.120. \cos 78^{o} 24' ≃ 64835 \Rightarrow A B ≃ 255.$

Câu 15:

20/07/2024

Hai chiếc tàu thuỷ cùng xuất phát từ vị trí A, đi thẳng theo hai hướng tạo với nhau một góc $60^{\circ}$ . Tàu thứ nhất chạy với tốc độ 30km/h, tàu thứ hai chạy với tốc độ 40km/h. Hỏi sau 2 giờ hai tàu cách nhau bao nhiêu km?

A. 13

B. $15 \sqrt{13} .$

C. $20 \sqrt{13}$

D. 15

Xem đáp án

Đáp án: C

Giải thích:

Lời giải

Không có đáp án.

Ta có: Sau 2h quãng đường tàu thứ nhất chạy được là: $S_{1} = 30.2 = 60 k m .$

Sau 2h quãng đường tàu thứ hai chạy được là: $S_{2} = 40.2 = 80 k m .$

Vậy: sau 2h hai tàu cách nhau là:

$S = \sqrt{{S_{1}}^{2} + {S_{2}}^{2} - 2 S_{1} . S_{2} . \cos 60^{0}} = 20 \sqrt{13} .$

Câu 16:

22/07/2024

Cho

\vec{O M} = (- 2; - 1)

,

\vec{O N} = (3; - 1)

. Tính góc của

(\vec{O M}, \vec{O N})

A. $135^{o}$ .

B. $- \frac{\sqrt{2}}{2}$ .

C. ${-135}^{o}$ .

D. $\frac{\sqrt{2}}{2}$ .

Xem đáp án

Đáp án: A

Giải thích:

Lời giải

Ta có

$\cos (\vec{O M}, \vec{O N}) = \frac{\vec{O M} . \vec{O N}}{|\vec{O M}| . \vec{|O N|}} = \frac{- 5}{\sqrt{5} . \sqrt{10}} = - \frac{\sqrt{2}}{2} \Rightarrow (\vec{O M}, \vec{O N}) = 135^{o}$

Câu 17:

12/07/2024

Tam giác ABC vuông ở A và có góc

\hat{B} = 50^{o}

. Hệ thức nào sau đây là sai?

A. $(\vec{A B}, \vec{B C}) = 130^{o}$ .

B. $(\vec{B C}, \vec{A C}) = 40^{o}$ .

C. $(\vec{A B}, \vec{C B}) = 50^{o}$ .

D. $(\vec{A C}, \vec{C B}) = 120^{o}$ .

Xem đáp án

Đáp án: D

Giải thích:

Lời giải

Phương án A:

$(\vec{A B}, \vec{B C}) = 180^{0} - (\vec{A B}, \vec{C B}) = 130^{o}$

nên loại A.

Phương án B:

$(\vec{B C}, \vec{A C}) = (\vec{C B}, \vec{C A}) = 40^{o}$

nên loại B.

Phương án C:

$(\vec{A B}, \vec{C B}) = (\vec{B A}, \vec{B C}) = 50^{o}$

nên loại C.

Phương án D:

$(\vec{A C}, \vec{C B}) = 180^{0} - (\vec{C A}, \vec{C B}) = 140^{o}$

nên chọn D.

Câu 18:

30/09/2024

Cho hình thang vuông ABCD có đáy lớn AB=4a, đáy nhỏ CD=2a, đường cao AD=3a. Tính

\vec{D A} . \vec{B C}

A. $- 9 a^{2}$ .

B. $15 a^{2}$ .

C. 0.

D. $9 a^{2}$

Xem đáp án

Đáp án đúng là: A

* Phương pháp giải

Áp dụng tích chất tích vô hướng của vecto

$\vec{a} . (\vec{b} + \vec{c}) = \vec{a} . \vec{b} + \vec{a} . \vec{c}$

* Lời giải

Vì:

$\vec{D A} . \vec{B C} = \vec{D A} . (\vec{B A} + \vec{A D} + \vec{D C}) = \vec{D A} . \vec{A D} = - 9 a^{2}$

nên chọn A.

*Lý thuyết liên quan

Hai vectơ cùng phương, cùng hướng, bằng nhau.

+ Đường thẳng đi qua điểm đầu và điểm cuối của một vectơ được gọi là giá của vectơ đó.

+ Hai vectơ được gọi là cùng phương nếu chúng có giá song song hoặc trùng nhau.

+ Đối với hai vectơ cùng phương thì chúng cùng hướng hoặc ngược hướng.

+ Hai vectơ và được gọi là bằng nhau, kí hiệu là $\vec{a}$ = $\vec{b}$ , nếu chúng có cùng độ dài và cùng hướng.

Chú ý:

+ Ta cũng xét các vectơ điểm đầu và điểm cuối trùng nhau (chẳng hạn $\vec{A A}$ , $\vec{B B}$ ), gọi là các vectơ–không.

+ Ta quy ước vectơ–không có độ dài bằng 0, cùng hướng (do đó cùng phương) với mọi vectơ.

+ Các vectơ–không có cùng độ dài và cùng hướng nên bằng nhau và được kí hiệu chung là $\vec{0}$ .

+ Với mỗi điểm O và vectơ $\vec{a}$ cho trước, có duy nhất điểm A sao cho $\vec{O A} = \vec{a}$ .

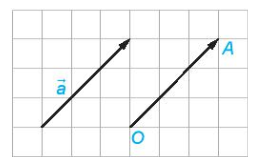
Nhận xét: Ba điểm phân biệt A, B, C thẳng hàng khi và chỉ khi $\vec{A B}$ và $\vec{A C}$ cùng phương.

Chú ý: Ta có thể dùng vectơ để biểu diễn các đại lượng như lực, vận tốc, gia tốc. Hướng của vectơ chỉ hướng của đại lượng, độ dài của vectơ thể hiện cho độ lớn của đại lượng và được lấy tỉ lệ với độ lớn của đại lượng.

Xem thêm các bài toán hay, chi tiết khác

Lý thuyết Toán 10 Bài 7: Các khái niệm mở đầu - Kết nối tri thức

Giải Toán 10 Bài 7 (Kết nối tri thức): Các khái niệm mở đầu

Câu 19:

13/07/2024

Cho tam giác ABC vuông tại C có AC=9,BC=5 . Tính

\vec{A B} . \vec{A C}

A. 9

B. 81

C. 3

D. 5

Xem đáp án

Đáp án: B

Giải thích:

Lời giải

Ta có :

$\vec{A B} . \vec{A C} = (\vec{A C} + \vec{C B}) . \vec{A C} = \vec{A C} . \vec{A C} + \vec{C B} . \vec{A C} = \vec{A C} . \vec{A C} = 81$

nên chọn B.

Câu 20:

23/07/2024

Cho hai vectơ

\vec{a}

và

\vec{b}

. Biết

|\vec{a}| = 2, |\vec{b}| = \sqrt{3}

và

(\vec{a}, \vec{b}) = 120^{o}

. Tính

|\vec{a} + \vec{b}|

A. $\sqrt{7 + \sqrt{3}}$ .

B. $\sqrt{7 - \sqrt{3}}$ .

C. $\sqrt{7 - 2 \sqrt{3}}$ .

D. $\sqrt{7 + 2 \sqrt{3}}$ .

Xem đáp án

Đáp án: C

Giải thích:

Lời giải

Ta có:

$|\vec{a} + \vec{b}| = \sqrt[]{{(\vec{a} + \vec{b})}^{2}} = \sqrt[]{{\vec{a}}^{2} + {\vec{b}}^{2} + 2 \vec{a} . \vec{b}} = \sqrt[]{{|\vec{a}|}^{2} + {|\vec{b}|}^{2} + 2 |\vec{a}| |\vec{b}| c o s (\vec{a}, \vec{b})} = \sqrt{7 - 2 \sqrt{3}}$

Câu 21:

13/07/2024

Cho hai điểm B, C phân biệt. Tập hợp những điểm M thỏa mãn

\vec{C M} . \vec{C B} = {\vec{C M}}^{2}

là

A. Đường tròn đường kính BC.

B. Đường tròn (B,BC).

C. Đường tròn (C,CB).

D. Một đường khác.

Xem đáp án

Đáp án: A

Giải thích:

Lời giải

$\vec{C M} . \vec{C B} = {\vec{C M}}^{2} \Leftrightarrow \vec{C M} . \vec{C B} - {\vec{C M}}^{2} = 0 \Leftrightarrow \vec{C M} . \vec{M B} = 0$

Tập hợp điểm M là đường tròn đường kính BC.

Câu 22:

23/07/2024

Trong mặt phẳng

(O; \vec{i}, \vec{j})

cho 2 vectơ:

\vec{a} = 3 \vec{i} + 6 \vec{j}

và

\vec{b} = 8 \vec{i} - 4 \vec{j .}

Kết luận nào sau đây sai?

A. $\vec{a} . \vec{b} = 0.$

B. $\vec{a} ⊥ \vec{b}$ .

C. $|\vec{a}| . |\vec{b}| = 0$ .

D. $|\vec{a} . \vec{b}| = 0$ .

Xem đáp án

Đáp án: C

Giải thích:

Lời giải

$\vec{a} = (3; 6); \vec{b} = (8; - 4)$

Phương án A:

$\vec{a} . \vec{b} = 24 - 24 = 0$ nên loại A

Phương án B: $\vec{a} . \vec{b} = 0$ suy ra $\vec{a}$ vuông góc $\vec{b}$ nên loại B

Phương án C: $|\vec{a}| . |\vec{b}|$

$= \sqrt[]{3^{2} + 6^{2}} . \sqrt[]{8^{2} + {(- 4)}^{2}} \neq 0$

nên chọn C.

Câu 23:

08/11/2024

Cho tam giác ABC có b = 7; c = 5,

\cos A = \frac{3}{5}

. Đường cao

h_{a}

của tam giác ABC là

A. $\frac{7 \sqrt{2}}{2} .$

B. 8

C. $8 \sqrt{3} .$

D. $80 \sqrt{3} .$

Xem đáp án

Đáp án đúng: A

*Lời giải:

Áp dụng định lí cosin trong tam giác ta có:

a²= b²+ c²= 2bc.cosA = 7²+ 5²- 2.7.5.3/5 = 32

Nên $a = 4 \sqrt{2}$

Mặt khác: sin²A + cos²A = 1 nên sin²A = 1 - cos²A = $\frac{16}{25}$

Mà sinA > 0 nên sinA = $\frac{4}{5}$

Mà: $S_{∆ A B C} = \frac{1}{2} b . c . \sin A = \frac{1}{2} a . h_{a}$

$\Rightarrow h_{a} = \frac{b c \sin A}{a} = \frac{7.5 . \frac{4}{5}}{4 \sqrt{2}} = \frac{7 \sqrt{2}}{2}$

*Phương pháp giải:

- Sử dụng định lí cosin trong tam giác khi biết được số đo hai cạnh và số đo của góc xen giữa hai cạnh đó.

- Sử dụng công thức lượng giác để tìm ra giá trị của góc cần tính.

- Áp dụng công thức tính diện tích tam giác.

Cho tam giác có BC = a, AC = b, AB = c với:

• $h_{a}, h_{b}, h_{c}$ là độ dài đường cao lần lượt tương ứng với các cạnh BC, CA, AB

S là diện tích tam giác.

Khi đó ta có các công thức tính diện tích tam giác ABC như sau:

$S = \frac{1}{2} a h_{a} = \frac{1}{2} b h_{b} = \frac{1}{2} c h_{c} S = \frac{1}{2} b c \sin A = \frac{1}{2} c a \sin B = \frac{1}{2} a b \sin C$

* Lý thuyết nắm thêm và các công thức để tính diện tích tam giác"

Công thức tính diện tích tam giác

Cho tam giác có BC = a, AC = b, AB = c với:

• $h_{a}, h_{b}, h_{c}$ là độ dài đường cao lần lượt tương ứng với các cạnh BC, CA, AB

• R là bán kính đường tròn ngoại tiếp tam giác;

• r là bán kính đường tròn nội tiếp tam giác;

• $p = \frac{a + b + c}{2}$ là nửa chu vi tam giác;

• S là diện tích tam giác.

Khi đó ta có các công thức tính diện tích tam giác ABC như sau:

$S = \frac{1}{2} a h_{a} = \frac{1}{2} b h_{b} = \frac{1}{2} c h_{c} S = \frac{1}{2} b c \sin A = \frac{1}{2} c a \sin B = \frac{1}{2} a b \sin C S = \frac{a b c}{4 R} S = p r S = \sqrt{p (p - a) (p - b) (p - c)}$

(Công thức Hê-rông)

$\to$ Dựa vào dữ kiện bài ra để sử dụng linh hoạt một trong các công thức ở trên.

Định lí Côsin

Đối với tam giác ABC, ta thường kí hiệu A, B, C là các góc của tam giác tại đỉnh tương ứng; a, b, c tương ứng là độ dài của các cạnh đối diện với đỉnh A, B, C; p là nửa chu vi; S là diện tích; R, r tương ứng là bán kính đường tròn ngoại tiếp, nội tiếp tam giác.

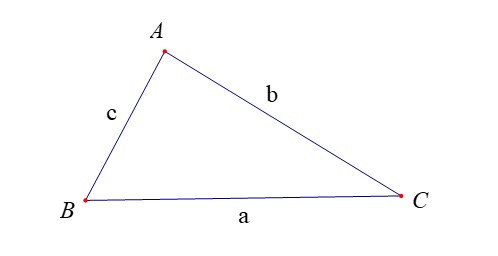
Hệ thức lượng trong tam giác (Lý thuyết + Bài tập Toán lớp 10) – Kết nối tri thức (ảnh 1)

Định lí Côsin. Trong tam giác ABC:

a2 = b2 + c2 – 2bc.cosA.

b2 = c2 + a2 – 2ca.cosB.

c2 = a2 + b2 – 2ab.cosC.

Định lí sin

Trong tam giác ABC: $\frac{a}{sinA} = \frac{b}{sinB} = \frac{c}{sinC} = 2 R$ .

Giải tam giác và ứng dụng thực tế

- Việc tính độ dài các cạnh và số đo các góc của một tam giác khi biết một số yếu tố của tam giác đó được gọi là giải tam giác.

Chú ý: Áp dụng định lí côsin, sin và sử dụng máy tính cầm tay, ta có thể tính (gần đúng) các cạnh và các góc của một tam giác trong các trường hợp sau:

+ Biết hai cạnh và góc xen giữa.

+ Biết ba cạnh.

+ Biết một cạnh và hai góc kề.

Xem thêm các bài viết liên quan hay, chi tiết:

Trắc nghiệm Các hệ thức lượng trong tam giác và giải tam giác (có đáp án)

Tóm tắt lý thuyết Toán lớp 10 Chương 3. Hệ thức lượng trong tam giác - Kết nối tri thức

Sách bài tập Toán 10 Bài 6 (Kết nối tri thức): Hệ thức lượng trong tam giác

Câu 24:

23/07/2024

Cho tam giác ABC, chọn công thức đúng trong các đáp án sau:

A. $m_{a}^{2} = \frac{b^{2} + c^{2}}{2} + \frac{a^{2}}{4} .$

B. $m_{a}^{2} = \frac{a^{2} + c^{2}}{2} - \frac{b^{2}}{4} .$

C. $m_{a}^{2} = \frac{a^{2} + b^{2}}{2} - \frac{c^{2}}{4} .$

D. $m_{a}^{2} = \frac{2 c^{2} + 2 b^{2} - a^{2}}{4} .$

Xem đáp án

Đáp án: D

Giải thích:

Lời giải

Ta có:

$m_{a}^{2} = \frac{b^{2} + c^{2}}{2} - \frac{a^{2}}{4} = \frac{2 b^{2} + 2 c^{2} - a^{2}}{4} .$

Câu 25:

22/07/2024

Cho tam giác ABC. Tìm công thức sai:

A. $\frac{a}{\sin A} = 2 R .$

B. $\sin A = \frac{a}{2 R} .$

C. $b \sin B = 2 R .$

D. $\sin C = \frac{c \sin A}{a} .$

Xem đáp án

Đáp án: C

Giải thích:

Lời giải

Ta có:

$\frac{a}{\sin A} = \frac{b}{\sin B} = \frac{c}{\sin C} = 2 R .$

Lớp 1 - Cánh diều

Tiếng Anh 1

Toán lớp 1

Tiếng Việt lớp 1

Lớp 1 - Chân trời sáng tạo

Tiếng Anh 1

Toán lớp 1

Tiếng Việt lớp 1

Lớp 1 - Kết nối tri thức

Tiếng Anh 1

Toán lớp 1

Tiếng Việt lớp 1

Tiện ích

Đọc sách online

Bộ đề ôn hè lớp 1 lên lớp 2

Giáo án lớp 1

Lớp 2 - Kết nối tri thức

Toán lớp 2

Tiếng Việt lớp 2

Đạo đức lớp 2

Tự nhiên và Xã hội lớp 2

Hoạt động trải nghiệm lớp 2

Tiếng Anh lớp 2

Âm nhạc lớp 2

Lớp 2 - Cánh diều

Toán lớp 2

Tiếng Việt lớp 2

Hoạt động trải nghiệm lớp 2

Tự nhiên và Xã hội lớp 2

Tiếng Anh lớp 2

Âm nhạc lớp 2

Đạo đức lớp 2

Lớp 2 - Chân trời sáng tạo

Toán lớp 2

Tiếng Việt lớp 2

Đạo đức lớp 2

Tự nhiên và Xã hội lớp 2

Hoạt động trải nghiệm lớp 2

Tiếng Anh lớp 2

Âm nhạc lớp 2

Đề thi các môn lớp 2

Đề thi các môn lớp 2 - Kết nối tri thức

Đề thi các môn lớp 2 - Cánh diều

Đề thi các môn lớp 2 - Chân trời sáng tạo

Tiện ích

Đọc sách online

Bộ đề ôn hè lớp 2 lên lớp 3

Giáo án lớp 2

Lớp 3 - Kết nối tri thức

Toán lớp 3

Tiếng Anh lớp 3

Tiếng Việt lớp 3

Đạo đức lớp 3

Tự nhiên và Xã hội lớp 3

Hoạt động trải nghiệm lớp 3

Âm nhạc lớp 3

Tin học lớp 3

Giáo dục thể chất lớp 3

Công nghệ lớp 3

Lớp 3 - Cánh diều

Toán lớp 3

Tiếng Việt lớp 3

Tiếng Anh lớp 3

Đạo đức lớp 3

Tự nhiên và Xã hội lớp 3

Hoạt động trải nghiệm lớp 3

Âm nhạc lớp 3

Tin học lớp 3

Giáo dục thể chất lớp 3

Công nghệ lớp 3

Lớp 3 - Chân trời sáng tạo

Toán lớp 3

Tiếng Việt lớp 3

Tiếng Anh lớp 3

Đạo đức lớp 3

Tự nhiên và Xã hội lớp 3

Hoạt động trải nghiệm lớp 3

Âm nhạc lớp 3

Tin học lớp 3

Giáo dục thể chất lớp 3