Giải Toán 11 trang 95 Tập 1 Chân trời sáng tạo
Với giải bài tập Toán 11 trang 95 trong Bài 1: Điểm, đường thẳng và mặt phẳng trong không gian sách Chân trời sáng tạo hay nhất, chi tiết giúp học sinh dễ dàng làm bài tập Toán 11 trang 95.
Giải Toán 11 trang 95 Tập 1
Lời giải:
Ta có:
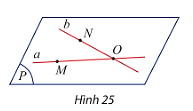
Hai điểm O và M thuộc mặt phẳng (P) nên đường thẳng a thuộc (P).
Hai điểm O và N thuộc mặt phẳng (P) nên đường thẳng b thuộc (P).
Vậy mặt phẳng (P) chứa cả hai đường thẳng a và b.
a) Tìm giao tuyến của hai mặt phẳng (M, a) và (M, b).
b) Lấy A, B lần lượt là hai điểm trên a, b và khác với điểm O. Tìm giao tuyến của (MAB) và mp(a, b).
Lời giải:
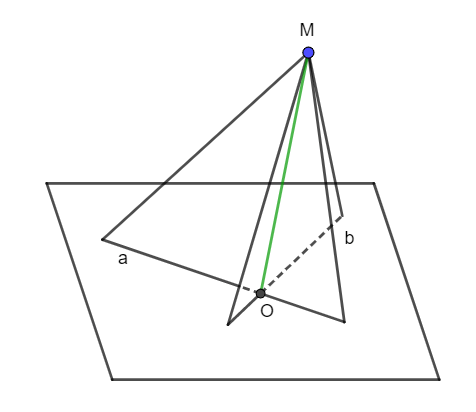
a) Ta có hình vẽ sau:
Ta có:
M ∈ mp(M, a) và M ∈ mp(M, b) nên M ∈ (M, a) ∩ (M, b).
O là giao điểm của hai đường thẳng a và b, mà a ⊂ mp(M, a) và b ⊂ mp(M, b) nên O ∈ (M, a) ∩ (M, b).
Vậy giao tuyến của hai mặt phẳng (M, a) và (M, b) là đường thẳng qua hai điểm M và O.
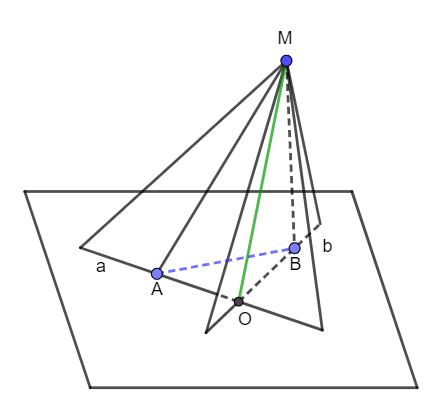
b)
Ta có: A ∈ (MAB) và A ∈ a ⊂ mp(a, b) nên A ∈ (MAB) ∩ mp(a, b).
Ta lại có: B ∈ (MAB) và B ∈ b ⊂ mp(a, b) nên B ∈ (MAB) ∩ mp(a, b).
Vậy giao tuyến của (MAB) và mp(a, b) là đường thẳng AB.
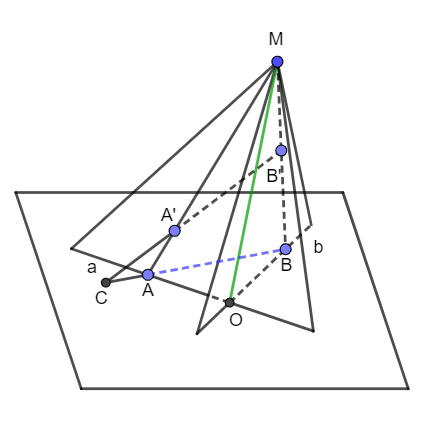
c)
Ta có (MA’B’) cũng là mặt phẳng (MAB)
Mà (MAB) giao mp(a, b) là đường thẳng AB nên điểm C cũng thuộc đường thẳng này do đó ba điểm A, B, C thẳng hàng.
Lời giải:
Qua bốn điểm không thẳng hàng ta có thể có được nhiều mặt phẳng đi qua bốn điểm này. Do đó chân ghế bốn chân hay bị khập khiễng.
Còn ghế ba chân có ba điểm tựa và qua ba điểm tựa này chỉ có thể có một mặt phẳng nên ghế ba chân không bị khập khiễng.
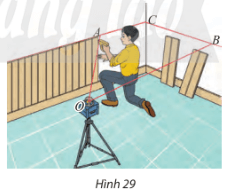
Lời giải:
Giao tuyến của mặt phẳng tạo bởi tia laser OA và OB với hai mặt tường lần lượt là AC và BC.
Xem thêm lời giải bài tập Toán 11 Chân trời sáng tạo hay, chi tiết khác:
Xem thêm lời giải bài tập Toán 11 Chân trời sáng tạo hay, chi tiết khác:
Thực hành 1 trang 89 Toán 11 Tập 1: a) Vẽ hình biểu diễn của một hình hộp chữ nhật. b) Quan sát Hình 4a và cho biết điểm nào thuộc, điểm nào không thuộc mặt phẳng (P)...
Thực hành 3 trang 90 Toán 11 Tập 1: Có bao nhiêu mặt phẳng đi qua ba đỉnh của tam giác MNP...
Hoạt động khám phá 10 trang 96 Toán 11 Tập 1: a) Các công trình kiến trúc, đồ vật trong Hình 30 có mặt bên là hình gì...
Hoạt động khám phá 11 trang 97 Toán 11 Tập 1: Trong Hình 34, hình chóp nào có số mặt ít nhất...
Xem thêm lời giải bài tập Toán 11 Chân trời sáng tạo hay, chi tiết khác:
Bài 2: Hai đường thẳng song song
Bài 3: Đường thẳng và mặt phẳng song song
Xem thêm các chương trình khác:
- Soạn văn lớp 11 Chân trời sáng tạo (hay nhất)
- Văn mẫu lớp 11 - Chân trời sáng tạo
- Tóm tắt tác phẩm Ngữ văn 11 – Chân trời sáng tạo
- Tác giả tác phẩm Ngữ văn lớp 11 - Chân trời sáng tạo
- Giải SBT Ngữ văn 11 – Chân trời sáng tạo
- Bố cục tác phẩm Ngữ văn 11 – Chân trời sáng tạo
- Giải Chuyên đề học tập Ngữ văn 11 – Chân trời sáng tạo
- Nội dung chính tác phẩm Ngữ văn lớp 11 – Chân trời sáng tạo
- Soạn văn 11 Chân trời sáng tạo (ngắn nhất)
- Giải sgk Tiếng Anh 11 – Friends Global
- Giải sbt Tiếng Anh 11 - Friends Global
- Trọn bộ Từ vựng Tiếng Anh 11 Friends Global đầy đủ nhất
- Bài tập Tiếng Anh 11 Friends Global theo Unit có đáp án
- Giải sgk Vật lí 11 – Chân trời sáng tạo
- Lý thuyết Vật lí 11 – Chân trời sáng tạo
- Giải sbt Vật lí 11 – Chân trời sáng tạo
- Giải Chuyên đề học tập Vật lí 11 – Chân trời sáng tạo
- Giải sgk Hóa học 11 – Chân trời sáng tạo
- Giải Chuyên đề học tập Hóa học 11 – Chân trời sáng tạo
- Lý thuyết Hóa 11 - Chân trời sáng tạo
- Giải sbt Hóa học 11 – Chân trời sáng tạo
- Giải sgk Sinh học 11 – Chân trời sáng tạo
- Lý thuyết Sinh học 11 – Chân trời sáng tạo
- Giải Chuyên đề học tập Sinh học 11 – Chân trời sáng tạo
- Giải sbt Sinh học 11 – Chân trời sáng tạo
- Giải sgk Giáo dục Kinh tế và Pháp luật 11 – Chân trời sáng tạo
- Giải Chuyên đề học tập Kinh tế pháp luật 11 – Chân trời sáng tạo
- Lý thuyết Kinh tế pháp luật 11 – Chân trời sáng tạo
- Giải sbt Kinh tế pháp luật 11 – Chân trời sáng tạo
- Giải sgk Lịch sử 11 – Chân trời sáng tạo
- Giải Chuyên đề học tập Lịch sử 11 – Chân trời sáng tạo
- Lý thuyết Lịch sử 11 - Chân trời sáng tạo
- Giải sbt Lịch sử 11 – Chân trời sáng tạo
- Giải sgk Địa lí 11 – Chân trời sáng tạo
- Giải Chuyên đề học tập Địa lí 11 – Chân trời sáng tạo
- Lý thuyết Địa lí 11 - Chân trời sáng tạo
- Giải sbt Địa lí 11 – Chân trời sáng tạo
- Giải sgk Hoạt động trải nghiệm 11 – Chân trời sáng tạo