Bài 3 trang 99 Toán 11 Tập 1 | Chân trời sáng tạo Giải Toán lớp 11

Lời giải Bài 3 trang 99 Toán 11 Tập 1 sách Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 11.

1 639 30/06/2023

Trang trước

Trang sau

Giải Toán 11 Bài 1: Điểm, đường thẳng và mặt phẳng trong không gian

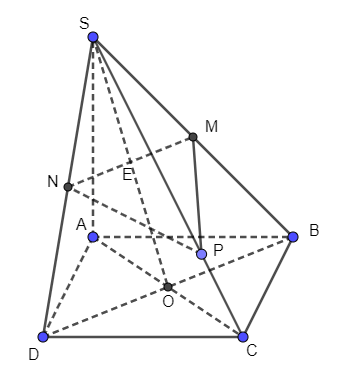
Bài 3 trang 99 Toán 11 Tập 1: Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi O là giao điểm của AC và BD; M và N lần lượt là trung điểm của SB và SD; P thuộc đoạn SC và không là trung điểm của SC.

a) Tìm giao điểm E của đường thẳng SO và mặt phẳng (MNP).

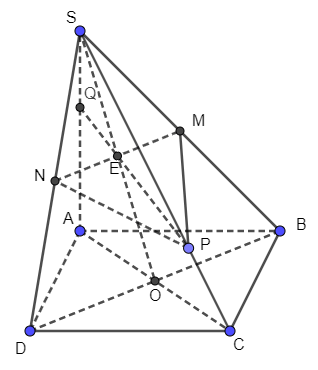
b) Tìm giao điểm Q của đường thẳng SA và mặt phẳng (MNP).

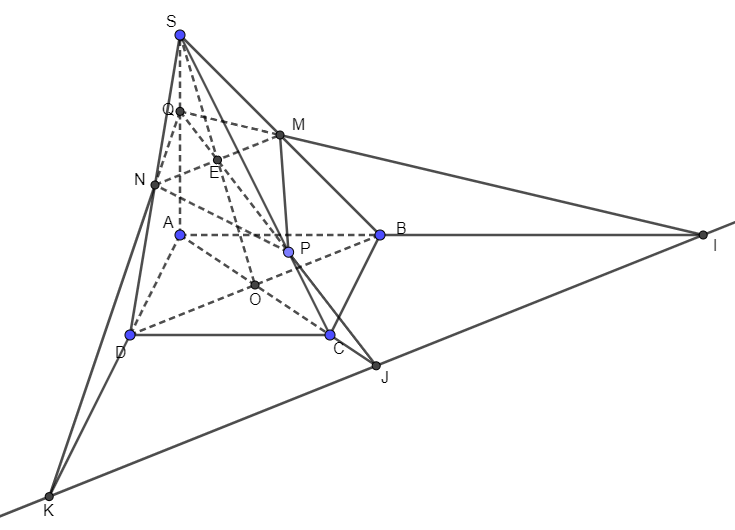
c) Gọi I, J, K lần lượt là giao điểm của QM và AB, QP và AC, QN và AD. Chứng minh I, J, K thẳng hàng.

Lời giải:

a) Gọi E là giao điểm của SO và MN

Mà MN ⊂ (MNP)

Suy ra SO ∩ (MNP) = {E}.

Bài 3 trang 99 Toán 11 Tập 1 Chân trời sáng tạo | Giải Toán 11

b)

Gọi Q là giao điểm của PE và SA

Mà PE ⊂ (MNP)

Suy ra SA ∩ (MNP) = {Q}.

Bài 3 trang 99 Toán 11 Tập 1 Chân trời sáng tạo | Giải Toán 11

c)

Ta có: QM ∩ AB = {I};

Mà QM ⊂ (QMN), AB ⊂ (ABCD)

Suy ra I ∈ (QMN) ∩ (ABC) (1)

Ta lại có: QN ∩ AD = {K}

Mà QN ⊂ (QMN), AD ⊂ (ABCD)

Suy ra K ∈ (QMN) ∩ (ABCD ) (2)

Từ (1) và (2) suy ra (QMN) ∩ (ABCD ) = {IM}.

Mặt khác, ta có: QE ∩ AC = {J}

Mà QE ⊂ (QMN), AC ⊂ (ABCD)

Suy ra J ∈ (QMN) ∩ (ABCD )

Do đó J thuộc đường thẳng IM.

Bài 3 trang 99 Toán 11 Tập 1 Chân trời sáng tạo | Giải Toán 11

Xem thêm lời giải bài tập Toán 11 Chân trời sáng tạo hay, chi tiết khác:

Hoạt động khởi động trang 88 Toán 11 Tập 1: Môn học Hình học phẳng tìm hiểu tính chất của các hình cùng thuộc một mặt phẳng...

Hoạt động khám phá 1 trang 88 Toán 11 Tập 1: Mặt bàn, mặt bảng cho ta hình ảnh của mặt phẳng. Hãy chỉ thêm các ví dụ khác về hình ảnh một phần của mặt phẳng...

Thực hành 1 trang 89 Toán 11 Tập 1: a) Vẽ hình biểu diễn của một hình hộp chữ nhật. b) Quan sát Hình 4a và cho biết điểm nào thuộc, điểm nào không thuộc mặt phẳng (P)...

Hoạt động khám phá 2 trang 89 Toán 11 Tập 1: Quan sát Hình 5 và cho biết muốn gác một cây sào tập nhảy cao, người ta cần dựa nó vào mấy điểm trên hai cọc đỡ...

Thực hành 2 trang 90 Toán 11 Tập 1: Cho bốn điểm A, B, C, D phân biệt, trong đó không có ba điểm nào thẳng hàng. Có bao nhiêu đường thẳng đi qua hai trong bốn điểm đã cho...

Hoạt động khám phá 3 trang 90 Toán 11 Tập 1: Quan sát Hình 7 và cho biết giá đỡ của máy ảnh tiếp đất tại mấy điểm. Tại sao giá đỡ máy ảnh thường có ba chân...

Thực hành 3 trang 90 Toán 11 Tập 1: Có bao nhiêu mặt phẳng đi qua ba đỉnh của tam giác MNP...

Hoạt động khám phá 4 trang 90 Toán 11 Tập 1: Quan sát Hình 10 và cho biết thợ mộc kiểm tra mặt bàn có phẳng hay không bằng một cây thước thẳng như thế nào...

Thực hành 4 trang 91 Toán 11 Tập 1: Cho mặt phẳng (Q) đi qua bốn đỉnh của tứ giác ABCD. Các điểm nằm trên đường chéo của tứ giác ABCD có thuộc mặt phẳng (Q) không? Giải thích...

Hoạt động khám phá 5 trang 91 Toán 11 Tập 1: Quan sát Hình 13 và cho biết bốn đỉnh A, B, C, D của cái bánh giò có cùng nằm trên một mặt phẳng hay không...

Thực hành 5 trang 91 Toán 11 Tập 1: Cho tam giác MNP và cho điểm O không thuộc mặt phẳng chứa ba điểm M, N, P...

Hoạt động khám phá 6 trang 92 Toán 11 Tập 1: Quan sát Hình 14 và mô tả phần giao nhau của hai bức tường...

Thực hành 6 trang 92 Toán 11 Tập 1: Cho A, B, C là ba điểm chung của hai mặt phẳng phân biệt (α) và (β) (Hình 16). Chứng mình A, B, C thẳng hàng...

Hoạt động khám phá 7 trang 92 Toán 11 Tập 1: Trong mặt phẳng (P), cho tam giác ABC có M, N lần lượt là trung điểm của các đoạn thẳng AB, AC (Hình 17). Tính tỉ số $\frac{M N}{B C}$ ...

Vận dụng 1 trang 93 Toán 11 Tập 1: Tại sao muốn cánh cửa đóng mở được êm thì các điểm gắn bản lề A, B, C của cánh cửa và mặt tường (Hình 19) phải cùng nằm trên một đường thẳng...

Hoạt động khám phá 8 trang 94 Toán 11 Tập 1: Cho đường thẳng a và điểm A không nằm trên a. Trên a lấy hai điểm B, C. Đường thẳng a có nằm trong mặt phẳng (ABC) không...

Hoạt động khám phá 9 trang 95 Toán 11 Tập 1: Hai đường thẳng phân biệt a và b cắt nhau tại điểm O. Trên a, b lấy lần lượt hai điểm M, N khác O...

Thực hành 7 trang 95 Toán 11 Tập 1: Cho hai đường thẳng a và b cắt nhau tại O và điểm M không thuộc mặt phẳng (a, b)...

Vận dụng 2 trang 95 Toán 11 Tập 1: Giải thích tại sao ghế bốn chân có thể bị khập khiễng còn ghế ba chân thì không...

Vận dụng 3 trang 95 Toán 11 Tập 1: Trong xây dựng, người ta thường dùng máy quét tia laser để kẻ các đường thẳng trên tường hoặc sàn nhà...

Hoạt động khám phá 10 trang 96 Toán 11 Tập 1: a) Các công trình kiến trúc, đồ vật trong Hình 30 có mặt bên là hình gì...

Hoạt động khám phá 11 trang 97 Toán 11 Tập 1: Trong Hình 34, hình chóp nào có số mặt ít nhất...

Thực hành 8 trang 98 Toán 11 Tập 1: Cho tứ diện SABC. Gọi H, K lần lượt là hai điểm trên hai cạnh SA và SC (H ≠ S, A; K ≠ S, C) sao cho HK không song song với AC...

Vận dụng 4 trang 98 Toán 11 Tập 1: Cho hình chóp S.ABCD. Trên các cạnh bên của hình chóp lấy lần lượt các điểm A’, B’, C’, D’. Cho biết AC cắt BD tại O, A’C’ cắt B’D’ tại O’...

Vận dụng 5 trang 98 Toán 11 Tập 1: Nêu cách tạo lập tứ diện đều SABC từ tam giác đều SS’S’’ theo gợi ý ở Hình 40...

Bài 1 trang 99 Toán 11 Tập 1: Cho hình chóp S.ABCD, gọi O là giao điểm của AC và BD. Lấy M, N lần lượt thuộc các cạnh SA, SC...

Bài 2 trang 99 Toán 11 Tập 1: Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi M là trung điểm của SC...

Bài 3 trang 99 Toán 11 Tập 1: Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi O là giao điểm của AC và BD; M và N lần lượt là trung điểm của SB và SD...

Bài 4 trang 99 Toán 11 Tập 1: Cho tứ diện ABCD. Gọi E, F, G lần lượt là ba điểm trên ba cạnh AB, AC, BD sao cho EF cắt BC tại I (I ≠ C), EG cắt AD tại H (H ≠ D)...

Bài 5 trang 99 Toán 11 Tập 1: Thước laser phát tia laser, khi tia này quay sẽ tạo ra mặt phẳng ánh sáng (Hình 41)...

Xem thêm lời giải bài tập Toán 11 Chân trời sáng tạo hay, chi tiết khác:

Bài tập cuối chương 3

Bài 2: Hai đường thẳng song song

Bài 3: Đường thẳng và mặt phẳng song song

Bài 4: Hai mặt phẳng song song

Bài 5: Phép chiếu song song

1 639 30/06/2023

Trang trước

Trang sau

Xem thêm các chương trình khác: