Nội dung bài viết

    Xem thêm

    Giải Toán 11 trang 87 Tập 2 Chân trời sáng tạo

    Với giải bài tập Toán 11 trang 87 Tập 2 trong Bài tập cuối chương 8 trang 86 sách Chân trời sáng tạo hay nhất, chi tiết giúp học sinh dễ dàng làm bài tập Toán 11 trang 87 Tập 2.

    1 416 21/12/2023
    Trang trước
    Chia sẻ
    Trang sau  

    Giải Toán 11 trang 87 Tập 2

    Bài 10 trang 87 Toán 11 Tập 2: Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SA ⊥ (ABCD) và SA = a. Gọi M, N, P lần lượt là trung điểm của SB, SC và SD. Tính khoảng cách giữa AM và NP.

    Lời giải:

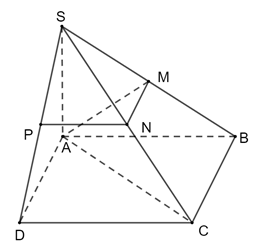
    Bài 10 trang 87 Toán 11 Tập 2 Chân trời sáng tạo | Giải Toán 11

    Vì SA ⊥ (ABCD) nên SA ⊥ BC

    Mà BC ⊥ AB nên BC ⊥ (SAB)

    Tam giác SBC có:

    M là trung điểm SB

    N là trung điểm SC

    Do đó MN là đường trung bình nên MN // BC, MN=12BC=a2 .

    Mà BC ⊥ (SAB) ⇒ MN ⊥ (SAB) ⇒ MN ⊥ AM.

    Tam giác SCD cóN là trung điểm SC; P là trung điểm SD

    Suy ra P là đường trung bình nên NP // CD.

    Mà MN // BC, BC ⊥ CD nên MN ⊥ NP.

    Vậy: d(AM,NP)=MN=a2

    Bài 11 trang 87 Toán 11 Tập 2: Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và D, AB = AD = 2a, CD = a; số đo góc nhị diện [S, BC, A] bằng 60°. Gọi I là trung điểm của cạnh AD. Biết hai mặt phẳng (SBI) và (SCI) cùng vuông góc với mặt phẳng (ABCD). Tính thể tích khối chóp S.ABCD theo a.

    Lời giải:

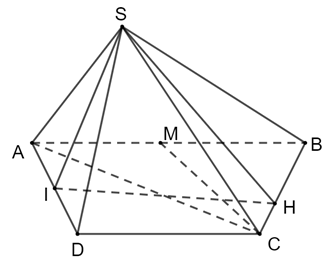
    Bài 11 trang 87 Toán 11 Tập 2 Chân trời sáng tạo | Giải Toán 11

    Kẻ IH ⊥ BC

    Ta có:

    SIB⊥(ABCD)(SIC)⊥(ABCD)(SIB)∩(SIC)=SI⇒SI⊥(ABCD)

    Suy ra: SI ⊥ BC mà BC ⊥ IH ⇒ BC ⊥ (SHI) ⇒ BC ⊥ SH.

    Lại có: [S,BC,A]=SHI^=60°.

    SABCD=12AB+CDAD=3a2;

    Ta có: I là trung điểm AD ⇒ AI=ID=12AD=a.

    SABI=12.AB.AI=a2

    SIDC=12.CD.ID=a22

    SIBC=SABCD−SAIB−SCID=3a22

    Gọi M là trung điểm của AB.

    ⇒BM=12AB=a, CM = AD = 2a ⇒BC=BM2+CM2=a5 ;

    ⇒IH=2SIBCBC=3a55 ⇒SI=IH.tan60°=3a155.

    Vậy VS.ABCD=13.SI.SABCD=3a3155.

    Bài 12 trang 87 Toán 11 Tập 2: Một chân cột bằng gang có dạng hình chóp cụt tứ giác đều có cạnh đáy lớn bằng 2a, cạnh đáy nhỏ bằng a, chiều cao h = 2a và bán kính đáy phần trụ rỗng bên trong bằng a2.

    a) Tìm góc phẳng nhị diện tạo bởi mặt bên và mặt đáy.

    b) Tính thể tích chân cột nói trên theo a.

    Lời giải:

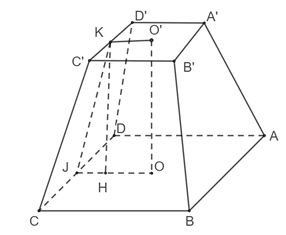
    Bài 12 trang 87 Toán 11 Tập 2 Chân trời sáng tạo | Giải Toán 11

    Mô hình hoá chân cột bằng gang bằng cụt chóp tứ giác đều ABCD.A′B′C′D′ với O, O′ là tâm của hai đáy. Vậy AB = 2a, A′B′ = a, OO′ = 2a.

    a) Gọi J, K lần lượt là trung điểm của CD, C′D′.

    • A′B′C′D′ là hình vuông nên O′K ⊥ C′D′.

    • CDD′C′ là hình thang cân nên JK ⊥ C′D.

    Vậy JKO'^ là góc phẳng nhị diện giữa mặt bên và đáy nhỏ, KJO^ là góc phẳng nhị diện giữa mặt bên và đáy lớn.

    b) Diện tích đáy lớn là: S=AB2=4a2.

    Diện tích đáy bé là: S'=A'B'2=a2.

    Thể tích hình chóp cụt là:

    V1=13hS+SS'+S'=14a33.

    Thể tích hình trụ rỗng là: V2=πR2h=πa32.

    Thể tích chân cột là: V=V1−V2=143−π2a3.

    Bài 13 trang 87 Toán 11 Tập 2: Cho hình hộp ABCD.A′B′C′D′ có cạnh bên AA′ = a, đáy ABCD là hình thoi có AB = BD = a. Hình chiếu vuông góc của A′ lên mặt đáy trùng với điểm O là giao điểm hai đường chéo của đáy. Tính thể tích của khối hộp.

    Lời giải:

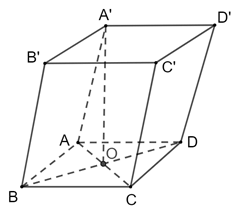
    Bài 13 trang 87 Toán 11 Tập 2 Chân trời sáng tạo | Giải Toán 11

    Xét tam giác ABD có AB = BD = AD = a nên ΔABD đều

    Suy ra BAD^=60°

    ABCD là hình thoi, O là trung điểm của BD

    ⇒BO=12BD=a2,AO=AB2−BO2=a32.

    Ta có: AA′ ⊥ (ABCD) ⇒ AA′ ⊥ AO .

    ⇒A'O=AA'2−AO2=a2

    SABCD=AB.AD.sinBAD^=a232

    VABCD.A'B'C'D'=A'O.SABCD=a334

    Xem thêm Lời giải bài tập Toán 11 Chân trời sáng tạo hay, chi tiết khác:

    Giải Toán 11 trang 86 Tập 2

    Giải Toán 11 trang 87 Tập 2

    Xem thêm Lời giải bài tập Toán 11 Chân trời sáng tạo hay, chi tiết khác: 

    Bài 1 trang 86 Toán 11 Tập 2: Cho hình chóp S.ABCD có đáy ABCD là hình vuông, SA vuông góc với mặt đáy. Đường thẳng CD vuông góc với mặt phẳng nào sau đây...

    Bài 2 trang 86 Toán 11 Tập 2: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh b, SA vuông góc với mặt đáy, SC=2b2. Số đo góc giữa cạnh bên SC và mặt đáy là...

    Bài 3 trang 86 Toán 11 Tập 2: Cho hình chóp S.ABCD có các cạnh bên và cạnh đáy đều bằng a. Gọi M là trung điểm của SA. Mặt phẳng (MBD) vuông góc với mặt phẳng nào dưới đây...

    Bài 4 trang 86 Toán 11 Tập 2: Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng và chiều cao bằng a2. Khoảng cách từ tâm O của đáy ABC đến một mặt bên là...

    Bài 5 trang 86 Toán 11 Tập 2: Thể tích của khối chóp cụt tam giác đều có cạnh đáy lớn bằng 2a, cạnh đáy nhỏ bằng a và chiều cao bằng a63 là...

    Bài 6 trang 86 Toán 11 Tập 2: Cho chóp tứ giác S.ABCD có đáy là hình chữ nhật với AB = 4a, AD = 3a. Các cạnh bên đều có độ dài 5a. Góc nhị diện [S, BC, A] có số đo là...

    Bài 7 trang 86 Toán 11 Tập 2: Nếu hình hộp chữ nhật có ba kích thước là 3, 4, 5 thì độ dài đường chéo của nó là...

    Bài 8 trang 86 Toán 11 Tập 2: Thể tích của khối lăng trụ tam giác đều có tất cả các cạnh đều bằng a là...

    Bài 9 trang 86 Toán 11 Tập 2: Cho hình vuông ABCD và tam giác đều SAB cạnh a nằm trong hai mặt phẳng vuông góc với nhau. Gọi M,N lần lượt là trung điểm của AB và AD...

    Bài 10 trang 87 Toán 11 Tập 2: Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SA ⊥ (ABCD) và SA = a. Gọi M, N, P lần lượt là trung điểm của SB, SC và SD...

    Bài 11 trang 87 Toán 11 Tập 2: Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và D, AB = AD = 2a, CD = a; số đo góc nhị diện [S, BC, A] bằng 60°...

    Bài 12 trang 87 Toán 11 Tập 2: Một chân cột bằng gang có dạng hình chóp cụt tứ giác đều có cạnh đáy lớn bằng 2a, cạnh đáy nhỏ bằng a, chiều cao h = 2a và bán kính đáy phần trụ rỗng...

    Bài 13 trang 87 Toán 11 Tập 2: Cho hình hộp ABCD.A′B′C′D′ có cạnh bên AA′ = a, đáy ABCD là hình thoi có AB = BD = a. Hình chiếu vuông góc của A′ lên mặt đáy trùng với điểm O...

    Xem thêm Lời giải bài tập Toán 11 Chân trời sáng tạo hay, chi tiết khác: 

    Bài 5: Góc giữa đường thẳng và mặt phẳng. Góc nhị diện

    Bài 1: Biến cố giao và quy tắc nhân xác suất

    Bài 2: Biến cố giao và quy tắc nhân xác suất

    Bài tập cuối chương 9 trang 98

    Bài 1: Vẽ hình khối bằng phần mềm GeoGebra. Làm kính 3D để quan sát ảnh nổi

    Tham khảo các loạt bài Toán 11 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 416 21/12/2023
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: