Nội dung bài viết

    Xem thêm

    Giải Toán 11 trang 86 Tập 2 Chân trời sáng tạo

    Với giải bài tập Toán 11 trang 86 Tập 2 trong Bài tập cuối chương 8 trang 86 sách Chân trời sáng tạo hay nhất, chi tiết giúp học sinh dễ dàng làm bài tập Toán 11 trang 86 Tập 2.

    1 280 21/12/2023
    Trang trước
    Chia sẻ
    Trang sau  

    Giải Toán 11 trang 86 Tập 2

    Bài 1 trang 86 Toán 11 Tập 2: Cho hình chóp S.ABCD có đáy ABCD là hình vuông, SA vuông góc với mặt đáy. Đường thẳng CD vuông góc với mặt phẳng nào sau đây?

    Bài 1 trang 86 Toán 11 Tập 2 Chân trời sáng tạo | Giải Toán 11

    A. (SAD).

    B. (SAC).

    C. (SAB).

    D. (SBD).

    Lời giải:

    Đáp án đúng là: A

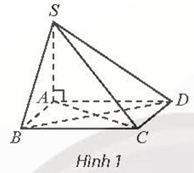
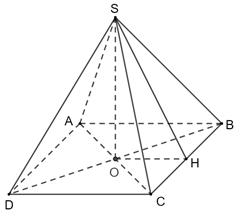
    Vì SA ⊥ (ABCD) nên SA ⊥ CD.

    Mà ABCD là hình vuông nên CD ⊥ AD.

    Do đó CD ⊥ (SAD).

    Bài 2 trang 86 Toán 11 Tập 2: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh b, SA vuông góc với mặt đáy, SC=2b2. Số đo góc giữa cạnh bên SC và mặt đáy là

    Bài 2 trang 86 Toán 11 Tập 2 Chân trời sáng tạo | Giải Toán 11

    A. 60°.

    B. 30°.

    C. 45°.

    D. 50°.

    Lời giải:

    Đáp án đúng là: A

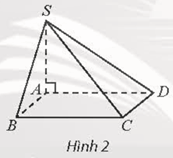
    Ta có SA ⊥ (ABCD) suy ra (SC, (ABCD)) = (SC, AC) = SCA^

    Mà ABCD là hình vuông nên AC=AB2+BC2=b2

    cosSCA^=ACSC=12⇒SCA^=60°.

    Vậy (SC, (ABCD)) = 60°

    Bài 3 trang 86 Toán 11 Tập 2: Cho hình chóp S.ABCD có các cạnh bên và cạnh đáy đều bằng a. Gọi M là trung điểm của SA. Mặt phẳng (MBD) vuông góc với mặt phẳng nào dưới đây?

    A. (SBC).

    B. (SAC).

    C. (SBD).

    D. (ABCD).

    Lời giải:

    Đáp án đúng là: B

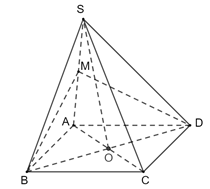
    Bài 3 trang 86 Toán 11 Tập 2 Chân trời sáng tạo | Giải Toán 11

    Gọi O là tâm của đáy.

    Khi đó SO ⊥ (ABCD) nên SO ⊥ BD

    Vì ABCD là hình vuông nên AC ⊥ BD. Khi đó:

    BD⊥SACBD⊂MBD ⇒MBD⊥SAC

    Bài 4 trang 86 Toán 11 Tập 2: Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng và chiều cao bằng a2. Khoảng cách từ tâm O của đáy ABC đến một mặt bên là

    A. a147 .

    B. a27 .

    C. a142 .

    D. 2a147 .

    Lời giải:

    Đáp án đúng là: A

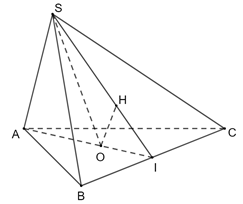
    Bài 4 trang 86 Toán 11 Tập 2 Chân trời sáng tạo | Giải Toán 11

    Gọi I là trung điểm của BC, kẻ OH ⊥ SI (H ∈ SI).

    Vì ΔABC là tam giác đều nên AI ⊥ BC

    Ta có: SO⊥(ABC) nên SO⊥BC

    ⇒ BC ⊥ (SAI) ⇒ BC ⊥ OH

    Mà OH ⊥ SI nên OH ⊥ (SBC)

    Do đó d(O, (SBC)) = OH

    ΔABC là tam giác đều ⇒AI=a3⇒OI=13AI=a33

    ΔOHI vuông tại O, OH là đường cao:

    1OH2=1SO2+1OI2⇒OH=a147

    Bài 5 trang 86 Toán 11 Tập 2: Thể tích của khối chóp cụt tam giác đều có cạnh đáy lớn bằng 2a, cạnh đáy nhỏ bằng a và chiều cao bằng a63 là

    A. 728a3 .

    B. 24a3 .

    C. 7212a3 .

    D. 734a3 .

    Lời giải:

    Đáp án đúng là: C

    Diện tích đáy lớn là: S=2a234=a23

    Diện tích đáy bé là: S'=a234

    Thể tích của bồn chứa là:

    V=13⋅a63⋅a23+a23⋅a234+a234=7212a3.

    Bài 6 trang 86 Toán 11 Tập 2: Cho chóp tứ giác S.ABCD có đáy là hình chữ nhật với AB = 4a, AD = 3a. Các cạnh bên đều có độ dài 5a. Góc nhị diện [S, BC, A] có số đo là

    A. 75°46′.

    B. 71°21′.

    C. 68°31′.

    D. 65°12′.

    Lời giải:

    Đáp án đúng là: D

    Bài 6 trang 86 Toán 11 Tập 2 Chân trời sáng tạo | Giải Toán 11

    Gọi O là tâm của đáy.

    Kẻ OH ⊥ BC (H ∈ BC)

    Vì ΔSAC cân tại S nên SO ⊥ AC.

    Vì ΔSBD cân tại S nên SO ⊥ BD.

    ⇒ SO ⊥ (ABCD) ⇒ SO ⊥ BC.

    Mà OH ⊥ BC nên SHO^ là góc nhị diện [S, BC, A].

    SABCD=AB.AD=12a2⇒SOBC=14SABCD=3a2.

    Mà SOBC=12.BC.OH⇒OH=2SOBCBC=2a.

    • AC=AB2+BC2=5a⇒OC=12AC=5a2.

    • SO=SC2−OC2=5a32.

    • tanSHO^=SOOH=534⇒SHO^≈65°12'.

    Bài 7 trang 86 Toán 11 Tập 2: Nếu hình hộp chữ nhật có ba kích thước là 3, 4, 5 thì độ dài đường chéo của nó là

    A. 52 .

    B. 50.

    C. 25 .

    D. 12.

    Lời giải:

    Đáp án đúng là: A

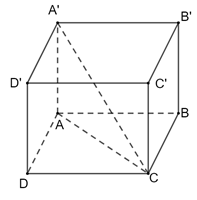
    Bài 7 trang 86 Toán 11 Tập 2 Chân trời sáng tạo | Giải Toán 11

    Giả sử hình hộp chữ nhật ABCD.A′B′C′D′ có AB = 3, BC = 4, AA′ = 5.

    • AC=AB2+BC2=5.

    • A'C=AA'2+AC2=52.

    Bài 8 trang 86 Toán 11 Tập 2: Thể tích của khối lăng trụ tam giác đều có tất cả các cạnh đều bằng a là

    A. a334 .

    B. a333 .

    C. a323 .

    D. a322 .

    Lời giải:

    Đáp án đúng là: A

    Diện tích đáy của khối lăng trụ là: S=a234.

    Chiều cao của khối lăng trụ là cạnh bên của lăng trụ bằng: h = a.

    Thể tích của khối lăng trụ là: V=Sh=a234.a=a334.

    Bài tập tự luận

    Bài 9 trang 86 Toán 11 Tập 2: Cho hình vuông ABCD và tam giác đều SAB cạnh a nằm trong hai mặt phẳng vuông góc với nhau. Gọi M,N lần lượt là trung điểm của AB và AD.

    a) Chứng minh rằng SMD⊥SNC.

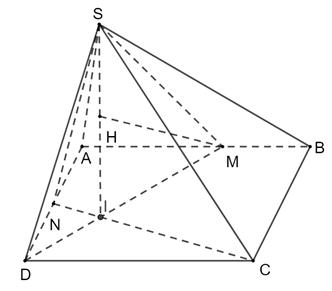
    b) Tính khoảng cách từ M đến mặt phẳng (SNC).

    Lời giải:

    Bài 9 trang 86 Toán 11 Tập 2 Chân trời sáng tạo | Giải Toán 11

    a) Tam giác SAB đều có M là trung điểm AB nên SM ⊥ AB. Mà (SAB) ⊥ (SAB) nên SM ⊥ (ABCD). Suy ra SM ⊥ NC.

    Xét ΔAMD và ΔDNC

    AM = DN

    MAD^=NDC^

    AD = DC

    Do đó ΔAMD và ΔDNC (c.g.c)

    Suy ra AMD^=CND^ (hai góc tương ứng)

    Mà AMD^+ADM^=90° nên CND^+ADM^=90°.

    Từ đó ta có tam giác DNI vuông tại I hay DM ⊥ NC. Mà SM ⊥ NC nên NC ⊥ (SND).

    Vậy (SNC) ⊥ (SMD).

    b) Kẻ MH ⊥ SI (H ∈ SI).

    Vì NC ⊥ (SMD) ⇒ NC ⊥ MH ⇒ MH ⊥ (SNC)

    Tam giác SAB đều có SM là trung tuyến nên SM=a32

    Tam giác CND vuông có DI là đường cao nên 1DI2=1DN2+1DC2.

    Suy ra DI=a55

    • DM=AM2+AD2=a55

    • MI=MD−DI=3a510

    Và SM ⊥ (ABCD) nên SM ⊥ MI.

    Tam giác SMI vuông tại M có MH là đường cao

    1MH2=1SM2+1MI2⇒MH=3a28

    Xem thêm Lời giải bài tập Toán 11 Chân trời sáng tạo hay, chi tiết khác:

    Giải Toán 11 trang 86 Tập 2

    Giải Toán 11 trang 87 Tập 2

    Xem thêm Lời giải bài tập Toán 11 Chân trời sáng tạo hay, chi tiết khác: 

    Bài 1 trang 86 Toán 11 Tập 2: Cho hình chóp S.ABCD có đáy ABCD là hình vuông, SA vuông góc với mặt đáy. Đường thẳng CD vuông góc với mặt phẳng nào sau đây...

    Bài 2 trang 86 Toán 11 Tập 2: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh b, SA vuông góc với mặt đáy, SC=2b2. Số đo góc giữa cạnh bên SC và mặt đáy là...

    Bài 3 trang 86 Toán 11 Tập 2: Cho hình chóp S.ABCD có các cạnh bên và cạnh đáy đều bằng a. Gọi M là trung điểm của SA. Mặt phẳng (MBD) vuông góc với mặt phẳng nào dưới đây...

    Bài 4 trang 86 Toán 11 Tập 2: Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng và chiều cao bằng a2. Khoảng cách từ tâm O của đáy ABC đến một mặt bên là...

    Bài 5 trang 86 Toán 11 Tập 2: Thể tích của khối chóp cụt tam giác đều có cạnh đáy lớn bằng 2a, cạnh đáy nhỏ bằng a và chiều cao bằng a63 là...

    Bài 6 trang 86 Toán 11 Tập 2: Cho chóp tứ giác S.ABCD có đáy là hình chữ nhật với AB = 4a, AD = 3a. Các cạnh bên đều có độ dài 5a. Góc nhị diện [S, BC, A] có số đo là...

    Bài 7 trang 86 Toán 11 Tập 2: Nếu hình hộp chữ nhật có ba kích thước là 3, 4, 5 thì độ dài đường chéo của nó là...

    Bài 8 trang 86 Toán 11 Tập 2: Thể tích của khối lăng trụ tam giác đều có tất cả các cạnh đều bằng a là...

    Bài 9 trang 86 Toán 11 Tập 2: Cho hình vuông ABCD và tam giác đều SAB cạnh a nằm trong hai mặt phẳng vuông góc với nhau. Gọi M,N lần lượt là trung điểm của AB và AD...

    Bài 10 trang 87 Toán 11 Tập 2: Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SA ⊥ (ABCD) và SA = a. Gọi M, N, P lần lượt là trung điểm của SB, SC và SD...

    Bài 11 trang 87 Toán 11 Tập 2: Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và D, AB = AD = 2a, CD = a; số đo góc nhị diện [S, BC, A] bằng 60°...

    Bài 12 trang 87 Toán 11 Tập 2: Một chân cột bằng gang có dạng hình chóp cụt tứ giác đều có cạnh đáy lớn bằng 2a, cạnh đáy nhỏ bằng a, chiều cao h = 2a và bán kính đáy phần trụ rỗng...

    Bài 13 trang 87 Toán 11 Tập 2: Cho hình hộp ABCD.A′B′C′D′ có cạnh bên AA′ = a, đáy ABCD là hình thoi có AB = BD = a. Hình chiếu vuông góc của A′ lên mặt đáy trùng với điểm O...

    Xem thêm Lời giải bài tập Toán 11 Chân trời sáng tạo hay, chi tiết khác: 

    Bài 5: Góc giữa đường thẳng và mặt phẳng. Góc nhị diện

    Bài 1: Biến cố giao và quy tắc nhân xác suất

    Bài 2: Biến cố giao và quy tắc nhân xác suất

    Bài tập cuối chương 9 trang 98

    Bài 1: Vẽ hình khối bằng phần mềm GeoGebra. Làm kính 3D để quan sát ảnh nổi

    Tham khảo các loạt bài Toán 11 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 280 21/12/2023
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: