Nội dung bài viết

    Xem thêm

    Giải Toán 10 trang 25 Tập 1 | Kết nối tri thức Giải Toán lớp 10

    Với giải bài tập Toán lớp 10 trang 25 Tập 1 trong Bài 3: Bất phương trình bậc nhất hai ẩn sách Kết nối tri thức hay nhất, chi tiết giúp học sinh dễ dàng làm bài tập Toán 10 trang 25 Tập 1.

    1 1,827 03/06/2023
    Trang trước
    Chia sẻ
    Trang sau  

    Giải Toán 10 trang 25 Tập 1

    Vận dụng trang 25 Toán 10 Tập 1: Một công ty viễn thông tính phí 1 nghìn đồng mỗi phút gọi nội mạng và 2 nghìn đồng mỗi phút gọi ngoại mạng. Em có thể sử dụng bao nhiêu phút gọi nội mạng và bao nhiêu phút gọi ngoại mạng trong một tháng nếu em muốn số tiền phải trả ít hơn 200 nghìn đồng?

    Lời giải

    Gọi số phút gọi nội mạng em sử dụng là x; số phút gọi ngoại mạng em sử dụng là y (x; y ≥ 0).

    Khi đó số tiền phải trả cho số phút gọi nội mạng là x (nghìn đồng); số tiền phải trả cho số phút gọi ngoại mạng là 2y (nghìn đồng).

    Tổng số tiền phải trả cho x phút gọi nội mạng và y phút gọi ngoại mạng là: x + 2y (nghìn đồng)

    Để số tiền phải trả ít hơn 200 nghìn đồng thì x; y phải thỏa mãn bất phương trình:

    x + 2y < 200.

    Do đó, muốn số tiền trả ít hơn 200 nghìn đồng thì số phút gọi nội mạng và số phút gọi ngoại mạng y phải là nghiệm của bất phương trình x + 2y < 200.

    Chẳng hạn với x = 50, y = 50 thì x + 2y = 50 + 2 . 50 = 150 < 200, do đó cặp số (50; 50) thỏa mãn bất phương trình x + 2y < 200 nên nếu gọi 50 phút nội mạng và 50 phút ngoại mạng thì số tiền phải trả sẽ ít hơn 200 nghìn đồng.  

    Bài tập

    Bài 2.1 trang 25 Toán 10 Tập 1: Bất phương trình nào sau đây là bất phương trình bậc nhất hai ẩn?

    a) 2x + 3y > 6;

    b) 22x + y ≤ 0;

    c) 2x2 – y ≥ 1.

    Lời giải

    a) 2x + 3y > 6 là bất phương trình bậc nhất hai ẩn vì nó có dạng ax + by > c.

    với a, b không đồng thời bằng 0.

    b) 22x + y ≤ 0⇔4x + y ≤ 0 là bất phương trình bậc nhất hai ẩn vì nó có dạng ax + by ≤ c, với a, b không đồng thời bằng 0.

    c) 2x2 – y ≥ 1 không là bất phương trình bậc nhất hai ẩn vì nó có x2 (ẩn x với bậc là 2) với hệ số khác 0.

    Bài 2.2 trang 25 Toán 10 Tập 1: Biểu diễn miền nghiệm của mỗi bất phương trình sau trên mặt phẳng tọa độ:

    a) 3x + 2y ≥ 300;

    b) 7x + 20y < 0.

    Lời giải

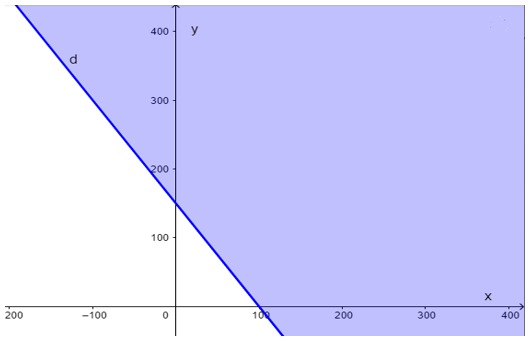
    a) Bước 1: Vẽ đường thẳng d: 3x + 2y = 300 trên mặt phẳng tọa độ.

    Bước 2: Lấy điểm O(0; 0) không thuộc đường thẳng d.

    Thay x = 0, y = 0 vào 3x + 2y ta được: 3.0 + 2.0 = 0 < 300.

    Do đó miền nghiệm của bất phương trình là nửa mặt phẳng có bờ là đường thẳng d không chứa điểm O (miền tô màu chứa đường thẳng d).

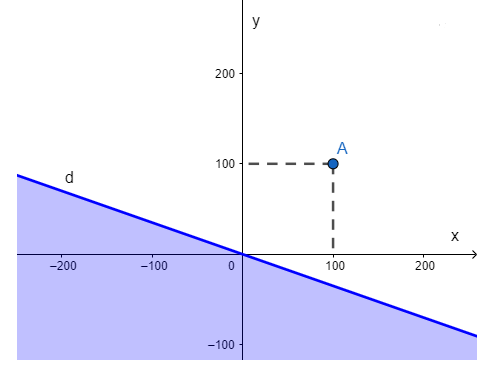
    Biểu diễn miền nghiệm của mỗi bất phương trình sau trên mặt phẳng tọa độ (ảnh 1)

    b) Bước 1: Vẽ đường thẳng d: 7x + 20y = 0 trên mặt phẳng tọa độ.

    Bước 2: Lấy điểm A(100; 100) không thuộc đường thẳng d.

    Thay x = 100, y = 100 vào 7x + 20y ta được: 7.100 + 20.100 = 2700 > 0.

    Do đó miền nghiệm của bất phương trình là nửa mặt phẳng có bờ là đường thẳng d không chứa điểm A (miền tô màu khôngchứa đường thẳng d).

    Biểu diễn miền nghiệm của mỗi bất phương trình sau trên mặt phẳng tọa độ (ảnh 1)

    Bài 2.3 trang 25 Toán 10 Tập 1: Ông An muốn thuê một chiếc ô tô (có lái xe) trong một tuần. Giá thuê xe được cho như bảng sau:

    Ông An muốn thuê một chiếc ô tô (có lái xe) trong một tuần. Giá thuê xe (ảnh 1)

    a) Gọi x và y lần lượt là số kilômét ông An đi trong các ngày từ thứ Hai đến thứ Sáu và trong hai ngày cuối tuần. Viết bất phương trình biểu thị mối liên hệ giữa x và y sao cho tổng số tiền ông An phải trả không quá 14 triệu đồng.

    b) Biểu diễn miền nghiệm của bất phương trình ở câu a trên mặt phẳng tọa độ.

    Lời giải

    a) Số tiền ông An phải trả cho việc thuê xe ô tô từ thứ Hai đến thứ Sáu là:

    900.5 + 8x = 4 500 + 8x (nghìn đồng).

    Số tiền ông An phải trả cho việc thuê xe ô tô từ thứ Bảy và Chủ nhật là:

    1 500.2 + 10y = 3 000 + 10y (nghìn đồng).

    Tổng số tiền ông An phải trả cho việc thuê xe trong một tuần là:

    4 500 + 8x + 3 000 + 10y = 7 500 + 8x + 10y (nghìn đồng).

    Để tổng số tiền ông An phải trả không quá 14 triệu đồng thì

    7 500 + 8x + 10y ≤ 14 000

    ⇔ 8x + 10y ≤ 6 500.

    ⇔ 4x + 5y ≤ 3 250.

    Vậy bất phương trình biểu thị mối liên hệ giữa x và y sao cho tổng số tiền ông An phải trả không quá 14 triệu đồng là 4x + 5y  ≤ 3 250.

    b)

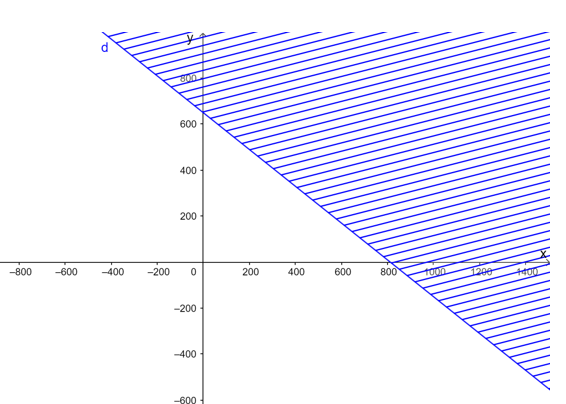
    Vẽ đường thẳng d: 4x + 5y = 3 250 trên mặt phẳng tọa độ.

    Lấy gốc tọa độ O(0; 0) và tính 4.0 + 5.0 = 0 < 3 250.

    Do đó miền nghiệm của bất phương trình là nửa mặt phẳng có bờ là đường thẳng d chứa gốc tọa độ và cả đường thẳng d (miền không bị gạch kể cả biên).

    Giải Toán 10 Bài 3: Bất phương trình bậc nhất hai ẩn - Kết nối tri thức (ảnh 1)

    Xem thêm lời giải bài tập Toán lớp 10 Kết nối tri thức với cuộc sống hay, chi tiết khác: 

    Giải Toán 10 trang 22 Tập 1

    Giải Toán 10 trang 23 Tập 1

    Giải Toán 10 trang 24 Tập 1

    Tham khảo các loạt bài Toán 10 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 1,827 03/06/2023
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: