Nội dung bài viết

    Xem thêm

    Hoạt động 4 trang 40 Toán 10 Tập 2 | Kết nối tri thức Giải Toán lớp 10

    Lời giải Hoạt động 4 trang 40 Toán 10 Tập 2 sách Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 10.

    1 531 02/03/2023
    Trang trước
    Chia sẻ
    Trang sau  

    Giải Toán 10 Kết nối tri thức Bài 20: Vị trí tương đối giữa hai đường thẳng. Góc và khoảng cách.

    Hoạt động 4 trang 40 Toán 10 Tập 2:

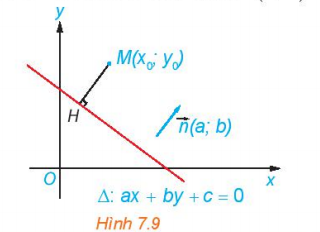
    Cho điểm M(x0; y0) và đường thẳng ∆ : ax + by + c = 0 có vectơ pháp tuyến n→(a; b). Gọi H là hình chiếu vuông góc của M lên ∆ (H.7.9).

    a) Chứng minh rằng n→.HM→=a2+b2.HM

    b) Gỉa sử H có toạ độ (x1; y1). Chứng minh rằng:

    n→.HM→=a.(x0−x1)+b(y0−y1)=ax0+by0+c

    c) Chứng minh rằng HM = ax0+by0+ca2+b2

    Giải Toán 10 Bài 20 (Kết nối tri thức): Vị trí tương đối giữa hai đường thẳng. Góc và khoảng cách. (ảnh 1) 

    Lời giải

    a) Ta có: n→.HM→= n→.MH→.cos(n→;HM→)=a2+b2.MH.cos(n→;HM→)

    Mà n→ và HM→ là hai vectơ cùng phương (vì cùng vuông góc với ∆) nên (n→;HM→)= 00

    Do đó, n→.HM→= a2+b2.MH.cos00= a2+b2.MH.

    Vậy n→.HM→=a2+b2.HM(*) (đpcm)

    b) Ta có: HM→= ( x0 – x1; y0 – y1)

    Mặt khác, ta có: n→.HM→= a.(x0 – x1) + b.(y0 – y1)

                                         = ax0 – ax1 + by0 – by1

          = ax0 + by0 – ax1 – by1 (1)

    Thoe giả thiết ta có điểm H thuộc đường thẳng ∆ nên ax1 + by1 + c = 0

                                                                                         ⇒ – ax1 – by1 = c (2)

    Thay (2) và (1) ta được: n→.HM→= a.(x0 – x1) + b.(y0 – y1) = ax0 + by0 + c (đpcm)

     Hay n→.HM→=ax0+by0+c (**)

    c) Từ (*) và (**) ta có: a2+b2.MH = ax0+by0+c ( = n→.HM→).

    ⇒ MH = ax0+by0+ca2+b2(đpcm).

    Xem thêm lời giải bài tập Toán lớp 10 Kết nối tri thức với cuộc sống hay, chi tiết khác:

    Hoạt động 1 trang 36 Toán 10 Tập 2: Trong mặt phẳng toạ độ, cho hai đường thẳng ∆1: x – 2y + 3 = 0 ∆2: 3x – y – 1 = 0... 

    Luyện tập 1 trang 37 Toán 10 Tập 2: Xét vị trí tương đối giữa các cặp đường thẳng sau: a) ∆1: x + 4y – 3 = 0 và ∆2: x – 4y – 3 = 0... 

    Hoạt động 2 trang 37 Toán 10 Tập 2: Hai đường thẳng ∆1 và ∆2 cắt nhau tạo thành bốn góc (H.7.6). Các số đo của bốn góc đó có mỗi quan hệ gì... 

    Hoạt động 3 trang 38 Toán 10 Tập 2: Cho hai đường thẳng cắt nhau ∆1 và ∆2 tương ứng có các vectơ pháp tuyến n1→,n2→... 

    Luyện tập 2 trang 39 Toán 10 Tập 2: Tính góc giữa hai đường thẳng ∆1: x + 3y + 2 = 0 và ∆2: y = 3x + 1... 

    Luyện tập 3 trang 39 Toán 10 Tập 2: Tính góc giữa hai đường thẳng ∆1:x=2+ty=1−2t và ∆ 2: x=1+t'y=5+3t'... 

    Luyện tập 4 trang 39 Toán 10 Tập 2: Cho đường thẳng ∆: y = ax + b với a ≠0. a) Chứng minh rằng ∆ cắt trục hoành... 

    Hoạt động 4 trang 40 Toán 10 Tập 2: Cho điểm M(x0; y0) và đường thẳng ∆: ax + by + c = 0 có vectơ pháp tuyến n→(a; b). Gọi H là hình chiếu vuông góc... 

    Trải nghiệm trang 40 Toán 10 Tập 2: Đo trực tiếp khoảng cách từ điểm M đến đường thẳng ∆ (H.7.10) và giải thích vì sao kết quả đo đạc đó phù hợp... 

    Luyện tập 5 trang 40 Toán 10 Tập 2: Tính khoảng cách từ điểm M(1; 2) đến đường thẳng ∆: x=5+3ty=−5−4t... 

    Vận dụng  trang 41 Toán 10 Tập 2: Nhân dịp nghỉ hè, Nam về quê ở với ông bà nội. Nhà ông bà nội có một ao cá có dạng hình chữ nhật ABCD... 

    Bài 7.7 trang 41 Toán 10 Tập 2: Xét vị trí tương đối giữa các cặp đường thẳng sau: a) ∆1 : 3 2x + 2y – 3 = 0... 

    Bài 7.8 trang 41 Toán 10 Tập 2: Tính góc giữa các cặp đường thẳng sau: a) ∆1 : 3x + y – 4 = 0 và ∆2 : x + 3y + 3 = 0... 

    Bài 7.9 trang 42 Toán 10 Tập 2: Trong mặt phẳng toạ độ Oxy cho điểm A(0; –2) và đường thẳng ∆: x + y – 4 = 0 a) Tính khoảng cách từ điểm A... 

    Bài 7.10 trang 42 Toán 10 Tập 2: Trong mặt phẳng toạ độ, cho tam giác ABC có A(1; 0), B(3; 2) và C(–2; –1) a) Tính độ dài đường cao kẻ từ đỉnh A... 

    Bài 7.11 trang 42 Toán 10 Tập 2: Chứng minh hai đường thẳng d: y = ax + b (a ≠ 0) và d’: y = a’x + b’ (a’ ≠0) vuông góc với nhau khi và chỉ khi aa’ = –1... 

    Bài 7.12 trang 42 Toán 10 Tập 2: Trong mặt phẳng toạ độ, một tín hiệu âm thanh phát đi từ một vị trí và được ba thiết bị ghi tín hiệu đặt tại 3 vị trí... 

    Xem thêm lời giải bài tập Toán lớp 10 Kết nối tri thức với cuộc sống hay, chi tiết khác:

    Bài 21: Đường tròn trong mặt phẳng tọa độ

    Bài 22: Ba đường Conic

    Bài tập cuối chương 7

    Bài 23: Quy tắc đếm

    Bài 24: Hoán vị, chỉnh hợp và tổ hợp

    Tham khảo các loạt bài Toán 10 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 531 02/03/2023
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: