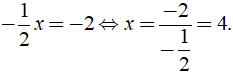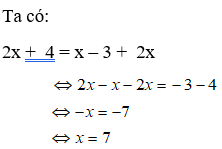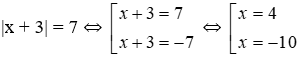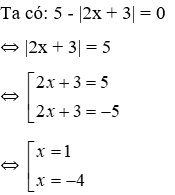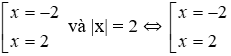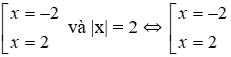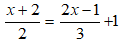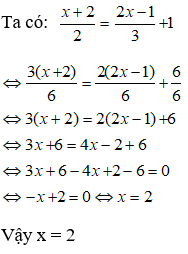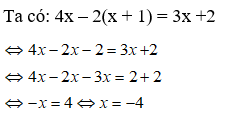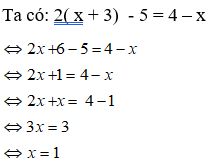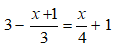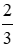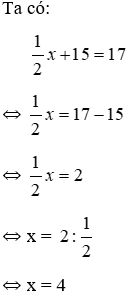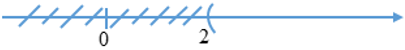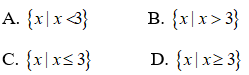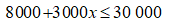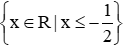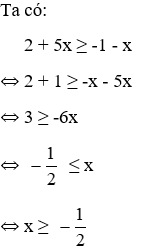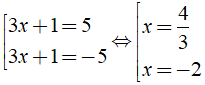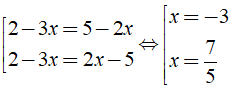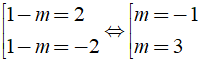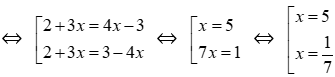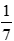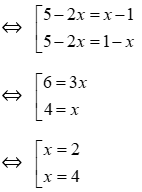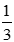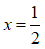Bài tập Toán lớp 8 Giữa học kì 2 có đáp án
Bài tập Toán lớp 8 Giữa học kì 2 có đáp án chi tiết giúp học sinh ôn luyện để đạt điểm cao trong bài thi Hóa học 8 Giữa học kì 1. Mời các bạn cùng đón xem:
[Năm 2023] Bài tập Toán lớp 8 Giữa học kì 2 có đáp án
Chương 3: Phương trình bậc nhất một ẩn
Bài tập Mở đầu về phương trình
Bài tập Phương trình bậc nhất một ẩn và cách giải
Bài tập Phương trình đưa được về dạng ax + b = 0
Bài tập Phương trình chứa ẩn ở mẫu
Bài tập Giải bài toán bằng cách lập phương trình
Chương 4: Bất phương trình bậc nhất một ẩn
Bài tập Liên hệ giữa thứ tự và phép cộng
Bài tập Liên hệ giữa thứ tự và phép nhân có đáp án
Bài tập Bất phương trình một ẩn
Bài tập Bất phương trình bậc nhất một ẩn
Bài tập Phương trình chứa dấu giá trị tuyệt đối
Bài tập Mở đầu về phương trình - Toán 8
I. Bài tập trắc nghiệm
Bài 1: Trong các phương trình sau, phương trình nào là phương trình một ẩn?
A. 2x = x + 1.
B. x + y = 3x.
C. 2a + b = 1.
D. xyz = xy.
Lời giải:
+ Một phương trình với ẩn x là hệ thức có dạng A( x ) = B( x ), trong đó A( x ) gọi là vế trái, B( x ) gọi là vế phải.
+ Nghiệm của phương trình là giá trị của ẩn x thoả mãn (hay nghiệm đúng) phương trình.
Nhận xét:
+ Đáp án A: là phương trình một ẩn là x
+ Đáp án B: là phương trình hai ẩn là x,y
+ Đáp án C: là phương trình hai ẩn là a,b
+ Đáp án D: là phương trình ba ẩn là x,y,z
Chọn đáp án A.
Bài 2: Nghiệm x = - 4 là nghiệm của phương trình ?
A. - 2,5x + 1 = 11.
B. - 2,5x = - 10
C. 3x - 8 = 0
D. 3x - 1 = x + 7
Lời giải:
+ Đáp án A: - 2,5x + 1 = 11 ⇔ - 2,5x = 10 ⇔ x = = - 4 → Đáp án A đúng.
+ Đáp án B: - 2,5x = - 10 ⇔ x = = 4 → Đáp án B sai.
+ Đáp án C: 3x - 8 = 0 ⇔ 3x = 8 ⇔ x = → Đáp án C sai.
+ Đáp án D: 3x - 1 = x + 7 ⇔ 3x - x = 7 + 1 ⇔ 2x = 8 ⇔ x = 4 → Đáp án D sai.
Chọn đáp án A.
Bài 3: Trong các phương trình sau, cặp phương trình nào tương đương?
A. x = 1 và x( x - 1 ) = 0
B. x - 2 = 0 và 2x - 4 = 0
C. 5x = 0 và 2x - 1 = 0
D. x2 - 4 = 0 và 2x - 2 = 0
Lời giải:
Hai phương trình tương đương nếu chúng có cùng một tập hợp nghiệm.
Đáp án A:
+ Phương trình x = 1 có tập nghiệm S = { 1 }
+ Phương trình x( x - 1 ) = 0 ⇔ có tập nghiệm là S = { 0;1 }
→ Hai phương trình không tương đương.
Đáp án B:
+ Phương trình x - 2 = 0 có tập nghiệm S = { 2 }
+ Phương trình 2x - 4 = 0 có tập nghiệm là S = { 2 }
→ Hai phương trình tương đương.
Đáp án C:
+ Phương trình 5x = 0 có tập nghiệm là S = { 0 }
+ Phương trình 2x - 1 = 0 có tập nghiệm là S = { }
→ Hai phương trình không tương đương.
Đáp án D:
+ Phương trình x2 - 4 = 0 ⇔ x = ± 2 có tập nghiệm là S = { ± 2 }
+ Phương trình 2x - 2 = 0 có tập nghiệm là S = { 1 }
→ Hai phương trình không tương đương.
Chọn đáp án B.
Bài 4: Tập nghiệm của phương trình 3x - 6 = 0 là ?
A. S = { 1 }
B. S = { 2 }
C. S = { - 2 }
D. S = { 1 }
Lời giải:
Ta có: 3x - 6 = 0 ⇔ 3x = 6 ⇔ x = 2
→ Phương trình có tập nghiệm là S = { 2 }
Chọn đáp án B.
Bài 5: Phương trình = - 2 có nghiệm là ?
A. x = - 2.
B. x = - 4.
C. x = 4.
D. x = 2.
Lời giải:
Ta có:
Vậy phương trình có tập nghiệm là x = 4.
Chọn đáp án C.
Bài 6: Giải phương trình: (2x + 4).(4 - x) = 0
A. S = {-2; 4}
B. S = {2; 4}
C. S = {2; - 4}
D. S = {-2; - 4}
Lời giải:
Ta có: (2x + 4).(4 - x) = 0 khi và chỉ khi:
(2x + 4) = 0 hoặc 4 – x = 0
* 2x + 4 = 0 khi x = -2
* 4 – x = 0 khi x = 4
Vậy tập nghiệm của phương trình là: S = {-2; 4}.
Chọn đáp án A
Bài 7: Hỏi x = 3 là nghiệm của phương trình nào?
A. 2x + 6 = 0
B. 6 – 2x = 0
C. 3 + x = 0
D. 3x + 1 = 0
Lời giải:
Xét phương án B: Với x = 3 thì
VT = 6 - 2x = 6 – 2.3 = 0 = VP
Do đó, x = 3 là nghiệm của phương trình 6 – 2x = 0
Chọn đáp án B
Bài 8: Phương trình 2x + 4 = x – 3 + 2x tương đương với phương trình nào sau đây ?
A. –x = 7
B. 2x + 4 = 0
C. –x = - 7
D. 2x – 4 = 0
Lời giải:
Chọn đáp án A
Bài 9: Phương trình x2 + 2x + 2 = (x - 2)2 có mấy nghiệm
A. 0
B. 1
C. 2
D. 3
Lời giải:
Chọn đáp án B
Bài 10: Tìm tập nghiệm của phương trình:
A. S = {11}
B. S = {-11}
C. S = ∅
D. S = {0}
Lời giải:
Chọn đáp án
II. Bài tập tự luận có lời giải
Bài 1: Có bao nhiêu nghiệm của phương trình |x + 3| = 7?
A. 2
B. 1
C. 0
D. 4
Lời giải
Ta có:
Vậy phương trình có hai nghiệm x = 4; x = -10
Đáp án cần chọn là: A
Bài 2 Số nghiệm của phương trình 5 - |2x + 3| = 0 là
A. 2
B. 1
C. 0
D. 4
Lời giải
Vậy phương trình có hai nghiệm x = 1; x = -4
Đáp án cần chọn là: A
Bài 3 Hai phương trình nào sau đây là hai phương trình tương đương?
A. x – 2 =4 và x + 1 = 2
B. x = 5 và x2 = 25
C. 2x2 – 8 = 0 và |x| = 2
D. 4 + x = 5 và x3 – 2x = 0
Lời giải
+) Xét x – 2 = 4 ⇔ x = 6 và x + 1 = 2 ⇔ x = 1 nên hai phương trình x – 2 =4 và x + 1 = 2 không tương đương
+) Xét phương trình x2 = 25 ⇔ x = ±5 nên phương trình x2 = 25 có hai nghiệm. Suy ra hai phương trình x = 5 và x2 = 25 không tương đương.
+) Xét phương trình 4 + x = 5 ⇔ x = 1, mà x = 1 không là nghiệm của phương trình x3 – 2x = 0 (vì 13 – 2.1= -1 ≠ 0) nên hai phương trình 4 + x = 5 và x3 – 2x = 0 không tương đương.
+) Xét phương trình 2x2 – 8 = 0 ⇔ 2x2 = 8 ⇔ x2 = 4 ⇔
Nhận thấy hai phương trình trên có cùng tập nghiệm {2; -2} nên chúng tương đương.
Bài 4 Số cặp phương trình tương đương trong các cặp phương trình sau là:
(I) x – 2 =4 và x + 1 = 2
(II) x = 5 và x2 = 25
(III) 2x2 – 8 = 0 và |x| = 2
(IV) 4 + x = 5 và x3 – 2x = 0
Lời giải
+) Xét x – 2 = 4 ⇔ x = 6 và x + 1 = 2 ⇔ x = 1 nên hai phương trình x – 2 =4 và x + 1 = 2 không tương đương
+) Xét phương trình x2 = 25 ⇔ x = ±5 nên phương trình x2 = 25 có hai nghiệm. Suy ra hai phương trình x = 5 và x2 = 25 không tương đương.
+) Xét phương trình 4 + x = 5 ⇔ x = 1, mà x = 1 không là nghiệm của phương trình x3 – 2x = 0 (vì 13 – 2.1= -1 ≠ 0) nên hai phương trình 4 + x = 5 và x3 – 2x = 0 không tương đương.
+) Xét phương trình 2x2 – 8 = 0 ⇔ 2x2 = 8 ⇔ x2 = 4 ⇔
Nhận thấy hai phương trình trên có cùng tập nghiệm {2; -2} nên chúng tương đương.
Vậy chỉ có 1 cặp phương trình tương đương trong các cặp đã cho
Bài 5 Phương trình nào nhận x = a (a là hằng số khác 0 và 1) làm nghiệm
Lời giải
Thay x = a vào từng phương trình ta được
+) 5.a – 3a = 2 ⇔ 2a = 2 ⇔ a = 1 (loại) nên x = a không là nghiệm của phương trình 5x – 3a = 2
+) a2 = a ⇔ 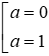
+) 
+) a2 – a.a = a2 – a2 = 0 nên x = a là nghiệm của phương trình x2 – a.x = 0
III. Bài tập vận dụng
Bài 1 Hãy cho ví dụ về:
a) Phương trình với ẩn y.
b) Phương trình với ẩn u.
Bài 2 Khi x = 6, tính giá trị mỗi vế của phương trình: 2x + 5 = 3(x – 1) + 2.
Bài 3 Cho phương trình 2(x + 2) – 7 = 3 – x
a) x = - 2 có thỏa mãn phương trình không ?
b) x = 2 có là một nghiệm của phương trình không ?
Bài 4 Với mỗi phương trình sau, hãy xét xem x = -1 có là nghiệm của nó không:
a) 4x - 1 = 3x - 2;
b) x + 1 = 2(x - 3);
c) 2(x + 1) + 3 = 2 - x
Bài 5 Trong các giá trị t = -1, t = 0 và t = 1, giá trị nào là nghiệm của phương trình: (t + 2)2 = 3t + 4?
Bài 6 Xét phương trình x + 1 = 1 + x. Ta thấy mọi số đều là nghiệm của nó. Người ta còn nói: Phương trình này nghiệm đúng với mọi x. Hãy cho biết tập nghiệm của phương trình đó.
Bài 7 Nối mỗi phương trình sau với các nghiệm của nó (theo mẫu):
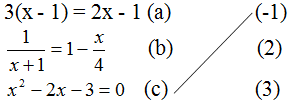
Bài 8 Hai phương trình x = 0 và x(x - 1) = 0 có tương đương không? Vì sao?
Bài tập Phương trình bậc nhất một ẩn và cách giải - Toán 8
I. Bài tập trắc nghiệm
Bài 1: Nghiệm của phương trình 2x - 1 = 3 là ?
A. x = - 2.
B. x = 2.
C. x = 1.
D. x = - 1.
Hướng dẫn:
Ta có: 2x - 1 = 3 ⇔ 2x = 1 + 3 ⇔ 2x = 4
⇔ x = ⇔ x = 2.
Vậy nghiệm của phương trình là x = 2.
Chọn đáp án B.
Bài 2: Nghiệm của phương trình + 3 = 4 là?
A. y = 2.
B. y = - 2.
C. y = 1.
D. y = - 1.
Hướng dẫn:
Ta có: + 3 = 4 ⇔ = 4 - 3 ⇔ = 1
⇔ y = 2.1 ⇔ y = 2.
Vậy nghiệm của phương trình là y = 2.
Chọn đáp án A.
Bài 3: Giá trị của m để phương trình 2x = m + 1 có nghiệm x = - 1 là ?
A. m = 3.
B. m = 1.
C. m = - 3
D. m = 2.
Hướng dẫn:
Phương trình 2x = m + 1 có nghiệm x = - 1
Khi đó ta có: 2.( - 1 ) = m + 1 ⇔ m + 1 = - 2 ⇔ m = - 3.
Vậy m = - 3 là giá trị cần tìm.
Chọn đáp án C.
Bài 4: Tập nghiệm của phương trình - 4x + 7 = - 1 là?
A. S = { 2 }.
B. S = { - 2 }.
C. S = { }.
D. S = { 3 }.
Hướng dẫn:
Ta có: - 4x + 7 = - 1 ⇔ - 4x = - 1 - 7 ⇔ - 4x = - 8
⇔ x = ⇔ x = 2.
Vậy phương trình có tập nghiệm là S = { 2 }.
Chọn đáp án A.
Bài 5: x = là nghiệm của phương trình nào sau đây?
A. 3x - 2 = 1.
B. 2x - 1 = 0.
C. 4x + 3 = - 1.
D. 3x + 2 = - 1.
Hướng dẫn:
+ Đáp án A: 3x - 2 = 1 ⇔ 3x = 3 ⇔ x = 1 → Loại.
+ Đáp án B: 2x - 1 = 0 ⇔ 2x = 1 ⇔ x = → Chọn.
+ Đáp án C: 4x + 3 = - 1 ⇔ 4x = - 4 ⇔ x = - 1 → Loại.
+ Đáp án D: 3x + 2 = - 1 ⇔ 3x = - 3 ⇔ x = - 1 → Loại.
Chọn đáp án B.
Bài 6: Giải phương trình:
A. x = 2
B. x = 1
C. x = -2
D. x = -1
Chọn đáp án A
Bài 7: Giải phương trình: 4x - 2(x + 1) = 3x + 2
A. x = 2
B. x = -3
C. x = - 4
D. x = 5
Chọn đáp án C
Bài 8: Tìm số nghiệm của phương trình sau: x + 2 - 2(x + 1) = -x
A. 0
B.1
C. 2
D. Vô số
Ta có: x + 2 - 2(x + 1) = -x
⇔ x + 2 - 2x - 2 = -x
⇔ -x = -x ( luôn đúng với mọi x)
Do đó, phương trình đã cho có vô số nghiệm.
Chọn đáp án D
Bài 9: Tìm tập nghiệm của phương trình sau: 2(x + 3) - 5 = 4 – x
A. S = {1}
B. S = 1
C. S = {2}
D. S = 2
Lời giải:
Chọn đáp án A
Bài 10: Phương trình sau có 1 nghiệm 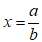
A. 22 B. 17
C. 27 D. 20
Lời giải:
Chọn đáp án C
II. Bài tập tự luận có lời giải
Bài 1: Phương trình 2x – 3 = 12 – 3x có bao nhiêu nghiệm?
Lời giải
Ta có 2x – 3 = 12 – 3x
⇔ 2x + 3x = 12 + 3
⇔ 5x = 15
⇔ x = 15 : 5
⇔ x = 3
Vậy phương trình có một nghiệm duy nhất x = 3
Bài 2 Số nghiệm của phương trình (x – 1)2 = x2 + 4x – 3 là:
Lời giải
(x – 1)2 = x2 + 4x – 3
⇔ x2 – 2x + 1 = x2 + 4x – 3
⇔ x2 – 2x + 1 – x2 – 4x + 3 = 0
⇔ -6x + 4 = 0
⇔ x =
Vậy phương trình có nghiệm duy nhất x =
Bài 3 Cho biết 2x – 2 = 0. Tính giá trị của 5x2 – 2.
Lời giải
Ta có
2x – 2 = 0
⇔ 2x = 2 ⇔ x = 1
Thay x = 1 vào 5x2 – 2 ta được: 5.12 – 2 = 5 – 2 = 3
Bài 4 Giả sử x0 là một số thực thỏa mãn 3 – 5x = -2. Tính giá trị của biểu thức S = ta đươc
Lời giải
Ta có 3 – 5x = -2
⇔ -5x = -2 – 3
⇔ -5x = -5 ⇔ x = 1
Khi đó x0 = 1, do đó S = 5.12 – 1 = 4
Bài 5 Tính giá trị của (5x2 + 1)(2x – 8) biết 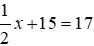
Lời giải
Thay x = 4 vào (5x2 + 1)(2x – 8) ta được: (5.42 + 1)(2.4 – 8) = (5.42 + 1).0 = 0
Bài 6 Giải các phương trình:
a) x – 4 = 0;
b) + x = 0;
c) 0,5 – x = 0.
Hướng dẫn giải chi tiết:
a) x – 4 = 0
⇔ x = 0 + 4
⇔ x = 4
Vậy phương trình có một nghiệm duy nhất x = 4
b) + x = 0
⇔ x = 0-
⇔ x =
Vậy phương trình có một nghiệm duy nhất x=
c) 0,5 – x = 0
⇔ x = 0,5-0
⇔ x = 0,5
Vậy phương trình có một nghiệm duy nhất x = 0,5
Bài 7 Giải các phương trình:
a) = -1;
b) 0,1x = 1,5;
c) -2,5x = 10.
Hướng dẫn giải chi tiết:
a) = -1
⇔ x = (-1).2
⇔ x = -2
Vậy phương trình có một nghiệm duy nhất x = -2
b) 0,1x = 1,5
⇔ x =
⇔ x = 15
Vậy phương trình có một nghiệm duy nhất x = 15
c) -2,5x = 10
⇔ x =
⇔ x = -4
Vậy phương trình có một nghiệm duy nhất x = - 4
Bài 8 Giải phương trình: -0,5x + 2,4 = 0.
Hướng dẫn giải chi tiết:
- 0,5x + 2,4 = 0
⇔ -0,5x = -2,4
⇔ x =
⇔ x = 4,8
Vậy phương trình có một nghiệm duy nhất x = 4,8
Bài 9 Tính diện tích S của hình thang ABCD theo x bằng hai cách:
1) Tính theo công thức: S = BH x (BC + DA) : 2
2) S = SABH + SBCKH + SCKD
Sau đó, sử dụng giả thiết S = 20 để thu được hai phương trình tương đương với nhau. Trong hai phương trình ấy, có phương trình nào là phương trình bậc nhất không?
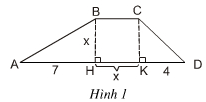
Hướng dẫn giải chi tiết:
1) Công thức: S = BH x (BC + DA) : 2
+ Có BH ⊥ HK, CK ⊥ HK (giả thiết)
Mà BC // HK (vì ABCD là hình thang)
Do đó: BH ⊥ BC, CK ⊥ BC
Tứ giác BCKH có bốn góc vuông nên BCKH là hình chữ nhật.
Mặt khác: BH = HK = x (giả thiết) nên BCKH là hình vuông.
⇒ BH = BC = CK = KH = x
+ AD = AH + HK + KD = 7 + x + 4 = 11 + x.
Vậy S = BH x (BC + DA) : 2 = x.(x + 11 + x) : 2 = x.(2x + 11) : 2 =
2) S = SABH + SBCKH + SCKD
+ ABH là tam giác vuông tại H
⇒ SBAH = .BH.AH = .7.x = .
+ BCKH là hình chữ nhật
⇒ SBCKH = x.x = x2.
+ CKD là tam giác vuông tại K
⇒ SCKD = .CK.KD = .4.x = 2x.
Do đó: S = SABH + SBCKH + SCKD = + x2 + 2x = x2 + .
- Với S = 20 ta có phương trình:
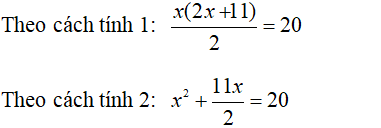
Hai phương trình trên tương đương với nhau. Và cả hai phương trình trên đều không phải là phương trình bậc nhất.
Bài 10 Hãy chỉ ra các phương trình bậc nhất trong các phương trình sau:
a) 1 + x = 0
b) x + x2 = 0
c) 1 – 2t = 0
d) 3y = 0
e) 0x – 3 = 0.
Hướng dẫn giải chi tiết:
Phương trình dạng ax+ b= 0, với a, b là hai số đã cho và a ≠ 0 , được gọi là phương trình bậc nhất một ẩn.
+ Phương trình 1 + x = 0 là phương trình bậc nhất với a = 1 ; b = 1.
+ Phương trình x + x2 = 0 không phải phương trình bậc nhất vì có chứa x2 bậc hai.
+ Phương trình 1 – 2t = 0 là phương trình bậc nhất ẩn t với a = -2 và b = 1.
+ Phương trình 3y = 0 là phương trình bậc nhất ẩn y với a = 3 và b = 0.
+ Phương trình 0x – 3 = 0 không phải phương trình bậc nhất vì hệ số bậc nhất a = 0.
III. Bài tập vận dụng
Bài 1 Giải các phương trình:
a) 4x – 20 = 0
b) 2x + x + 12 = 0
c) x – 5 = 3 – x
d) 7 – 3x = 9 – x
Bài 2 Giải các phương trình sau, viết số gần đúng của mỗi nghiệm ở dạng số thập phân bằng cách làm tròn đến hàng phần trăm.
a) 3x – 11 = 0
b) 12 + 7x = 0
c) 10 – 4x = 2x – 3
Bài 3 Giải phương trình x + 3 = 0
Bài 4 Giải phương trình = - 2.
Bài 5 Giải các phương trình
a) 4x – 20 = 0
b) 2x + x + 12 = 0
c) x – 5 = 3 – x
d) 7 – 3x = 9 – x
Bài 6 Giải các phương trình:
a) x – 4 = 0;
b) + x = 0;
c) 0,5 – x = 0.
Bài 7 Giải các phương trình:
a) = -1;
b) 0,1x = 1,5;
c) -2,5x = 10.
Bài 8 Giải phương trình: -0,5x + 2,4 = 0.
Bài tập Bất phương trình một ẩn - Toán 8
I. Bài tập trắc nghiệm
Bài 1: Nghiệm x = 3 là nghiệm của bất phương trình nào sau đây?
A. 5 - x < 1
B. 3x + 1 < 4
C. 4x - 11 > x
D. 2x - 1 > 3
Ta có:
+ 5 - x < 1 ⇔ 4 < x
+ 3x + 1 < 4 ⇔ 3x < 3 ⇔ x > 1
+ 4x - 11 > x ⇔ 3x > 11 ⇔ x >
+ 2x - 1 > 3 ⇔ 2x > 4 ⇔ x > 2
Vậy x = 3 là nghiệm của bất phương trình 2x - 1 > 3
Chọn đáp án D.
Bài 2: Tập nghiệm nào sau đây là tập nghiệm của bất phương trình: x ≤ 2 ?
A. S = { x| x ≥ 2 }.
B. S = { x| x ≤ 2 }.
C. S = { x| x ≥ - 2 }.
D. S = { x| x < 2}.
Tập nghiệm của bất phương trình: x ≤ 2 là S = { x| x ≤ 2 }.
Chọn đáp án B.
Bài 3: Hình vẽ sau là tập nghiệm của bất phương trình nào?
A. 2x - 4 < 0
B. 2x - 4 > 0
C. 2x - 4 ≤ 0
D. 2x - 4 ≥ 0
Ta có:
+ 2x - 4 < 0 ⇔ x < 2
+ 2x - 4 > 0 ⇔ x > 2
+ 2x - 4 ≤ 0 ⇔ x ≤ 2
+ 2x - 4 ≥ 0 ⇔ x ≥ 2
Chọn đáp án B.
Bài 4: Cho bất phương trình 3x - 6 > 0. Trong các bất phương trình sau, bất phương trình nào tương đương với bất phương trình đã cho?
A. 2x - 4 < 0
B. 2x - 4 ≥ 0
C. x > 2
D. 1 - 2x < 1
Ta có: 3x - 6 > 0 ⇔ 3x > 6 ⇔ x > 2
Vậy bất phương trình x > 2 tương đương với bất phương trình đã cho.
Chọn đáp án C.
Bài 5: Hỏi x = 2 là nghiệm của bất phương trình nào trong các bất phương trình sau:
A. x + 2 > 4
B. 4 -2x < 4
C. 4x – 2 < 2
D. x - 10 > 2
* Thay x = 2 vào bất phương trình x + 2 > 4 ta được: 2 + 2 > 4 là khẳng định sai nên x = 2 không là nghiệm của bất phương trình.
* Thay x = 2 vào bất phương trình 4 -2x < 4 ta được: 4 – 2.2 < 4 là khẳng định đúng nên x = 2 là nghiệm của bất phương trình.
* Thay x = 2 vào bất phương trình 4x - 2 < 2 ta được: 4.2 - 2 < 2 là khẳng định sai nên x = 2 không là nghiệm của bất phương trình.
* Thay x = 2 vào bất phương trình x -10 > 2 ta được: 2 - 10 > 2 là khẳng định sai nên x = 2 không là nghiệm của bất phương trình.
Chọn đáp án B
Bài 6: Hình vẽ sau biểu diễn tập nghiệm của bất phương trình nào ?
Trong hình vẽ trên tất cả các điểm bên trái điểm 3 bị gạch bỏ nên hình vẽ đã cho biểu diễn tập nghiệm {x | x ≥ 3}
Chọn đáp án D
Bài 7: Hình vẽ sau biểu diễn tập nghiệm nào?
Trong hình vẽ trên các điểm bên phải điểm 4 và số 4 bị gạch nên hình vẽ biểu diễn tập nghiệm: {x | x < 4}
Chọn đáp án A
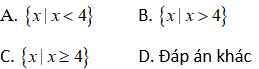
Bài 8: Hình vẽ sau biểu diễn tập nghiệm nào?
Các điểm bên phải điểm -2 bị gạch nên hình vẽ trên biểu diễn tập nghiệm : {x | x ≤ -2}
Chọn đáp án C
Bài 9: Lập bất phương trình cho bài toán sau:
Cô Lan chia đều 20 cái kẹo cho 4 bạn nhỏ. Hỏi mỗi bạn được bao nhiêu cái kẹo để sau khi chia xong cô Lan vẫn còn kẹo?
A. 4x < 20
B. 4x > 20
C. 20x < 4
D. 20x > 4
Trong đó , x là số kẹo mỗi bạn nhận được.
Gọi số kẹo mỗi bạn nhận được là x ( cái kẹo)
Khi đó, 4 bạn sẽ có tất cả: 4x ( cái kẹo)
Để sau khi chia xong, cô Lan vẫn còn kẹo thì 4x < 20
Chọn đáp án A
Bài 10: Bạn Huyền có 30 000 đồng,Huyền muốn mua 1 cái bút giá 8000 đồng và x quyển vở, biết giá mỗi quyển vở là 3000 đồng. Lập bất phương trình liên quan ẩn x?
Giá của x quyển vở là: 3000.x đồng
Tổng số tiền mua 1 cái bút và x quyển vở là: 8000 + 3 000x (đồng)
Vì số tiền bạn Huyền có là 30000 đồng nên ta có:
Chọn đáp án B
II. Bài tập tự luận có giải
Bài 1: Hãy chọn câu đúng. Tập nghiệm của bất phương trình 1 - 3x ≥ 2 - x là?
Lời giải
1 - 3x ≥ 2 - x
⇔ 1 - 3x + x - 2 ≥ 0
⇔ -2x - 1 ≥ 0
⇔ -2x - 1
⇔ x ≤ -
Vậy nghiệm của bất phương trình S =
Bài 2 Hãy chọn câu đúng. Bất phương trình 2 + 5x ≥ -1 - x có nghiệm là?
Lời giải
Vậy bất phương trình có nghiệm x ≥ -
Bài 3 Hãy chọn câu đúng, x = -3 là một nghiệm của bất phương trình?
Lời giải
+ Thay x = -3 vào bất phương trình 2x + 1 > 5 ta được
2. (-3) + 1 > 5 ⇔ -5 > 5 (vô lý) nên x = -3 không là nghiệm của bất phương trình 2x + 1 > 5.
+ Thay x = -3 vào bất phương trình 7 - 2x < 10 - x ta được
7 - 2. (-3) < 10 - (-3) ⇔ 13 < 13 (vô lý) nên x = -3 không là nghiệm của bất phương trình 7 - 2x < 10 - x.
+ Thay x = -3 vào bất phương trình 2 + x < 2 + 2x ta được
2 + (-3) < 2 + 2. (-3) ⇔ -1 < -4 (vô lý) nên x = -3 không là nghiệm của bất phương trình 2 + x < 2 + 2x.
+ Thay x = -3 vào bất phương trình -3x > 4x + 3 ta được
-3. (-3) > 4. (-3) + 3 ⇔ 9 > -9 (luôn đúng) nên x = -3 là nghiệm của bất phương trình -3x > 4x + 3.
Bài 4 Hãy chọn câu đúng, x = -3 không là nghiệm của bất phương trình nào dưới đây?
Lời giải
Thay x = -3 vào từng bất phương trình ta được:
Đáp án A: 2. (-3) + 1 = -5 > -5 (vô lí) nên x = -3 không là nghiệm của bất phương trình.
Đáp án B: VT = 7 - 2. (-3) = 14, Vp = 10 - (-3) = 13 nên 13 ≤ 13 (đúng) nên x = -3 là nghiệm của bất phương trình.
Đáp án C: VT = 3. (-3) - 2 = -11, VP = 6 - 2. (-3) = 12 nên -11 ≤ 12 (đúng) nên x = -3 là nghiệm của bất phương trình.
Đáp án D: VT = -3. (-3) = 9, VP = 4. (-3) + 3 = -9 nên 9 > -9 (đúng) nên x = -3 là nghiệm của bất phương trình.
Bài 5 Hình vẽ dưới dây biểu diễn tập nghiệm của bất phương trình nào?
Lời giải
Giải từng bất phương trình ta được
+) 2(x - 1) < x ⇔ 2x - 2 < x ⇔ 2x - x < 2 ⇔ x < 2
+) 2(x - 1) ≤ x - 4 ⇔ 2x - 2 ≤ x - 4 ⇔ 2x - x < -4 + 2 ⇔ x ≤ -2
+) 2x < x - 4 ⇔ 2x - x < -4 ⇔ x < -4
+) 2(x - 1) < x - 4 ⇔ 2x - 2 < x - 4 ⇔ 2x - x < -4 + 2 ⇔ x < -2
* Hình vẽ biểu diễn tập nghiệm S = {x < -2}.
Nên bất phương trình 2(x - 1) < x - 4 thỏa mãn.
Bài 6 Mỗi khẳng định sau đúng hay sai? Vì sao
a) (-6).5 < (-5).5 ;
b) (-6).(-3) < (-5).(-3);
c) (-2003).(-2005) ≤ (-2005).2004;
d) -3x2≤ 0.
Lời giải:
a) Ta có: -6 < -5
⇒ (-6).5 < (-5).5 (Nhân cả hai vế với 5 > 0 được BĐT cùng chiều).
⇒ Khẳng định a) đúng.
b) -6 < -5
⇒ (-6).(-3) > (-5).(-3) (Nhân cả hai vế với -3 < 0, BĐT đổi chiều).
⇒ Khẳng định b) sai.
c) -2003 < 2004
⇒ (-2003).(-2005) > (-2005).2004 (Nhân cả hai vế với -2005 < 0, BĐT đổi chiều)
⇒ Khẳng định c) sai.
d) x2≥ 0 với mọi x ∈
⇒ (-3).x2 ≤ (-3).0 (Nhân cả hai vế với -3 < 0, BĐT đổi chiều).
hay -3x2 ≤ 0.
⇒ Khẳng định d) đúng với mọi số thực x.
Bài 7 Cho a < b, hãy so sánh:
2a và 2b; 2a và a + b; -a + b; -a và -b.
Lời giải:
+ a < b ⇒ 2a < 2b (nhân cả 2 vế với 2 > 0, BĐT không đổi chiều).
+ a < b ⇒ a + a < b + a (Cộng cả 2 vế với a)
hay 2a < a + b.
+ a < b ⇒ (-1).a > (-1).b (Nhân cả 2 vế với -1 < 0, BĐT đổi chiều).
hay –a < -b.
Bài 8 Số a là số âm hay dương nếu:
12a < 15 a ? 4a < 3a ? -3a > -5a?
Lời giải:
a) Ta có: 12 < 15 (*). Để có bất đẳng thức cùng chiều là 12a < 15a ta phải nhân cả 2 vế của (*) với số dương. Vậy a là số dương.
b) Ta có: 4 > 3 (**). Để có bất đẳng thức trái chiều là 4a < 3a ta phải nhân cả 2 vế của (**) với số âm. Vậy a là số âm.
c) Ta có: -3 > -5 (***). Để có bất đẳng thức cùng chiều là -3a > -5a ta phải nhân cả 2 vế của (*) với số dương. Vậy a là số dương.
Bài 9 Cho a < b, chứng tỏ:
a) 2a - 3 < 2b - 3; b) 2a - 3 < 2b + 5.
Lời giải:
a) Ta có: a < b
⇒ 2a < 2b (Nhân cả hai vế với 2 > 0, BĐT không đổi chiều).
⇒ 2a – 3 < 2b – 3 (Cộng cả hai vế với -3, BĐT không đổi chiều).
Vậy 2a – 3 < 2b – 3.
b) Ta có: -3 < 5
⇒ 2b - 3 < 2b + 5 (cộng vào 2 vế với 2b)
mà 2a - 3 < 2b - 3 (chứng minh ở câu a))
Vậy: 2a - 3 < 2b + 5 (Tính chất bắc cầu).
Bài 10
a) Nhân cả hai vế của bất đẳng thức -2 < 3 với 5091 thì được bất đẳng thức nào ?
b) Dự đoán kết quả: Nhân cả hai vế của bất đẳng thức -2 < 3 với số c dương thì ta được bất đẳng thức nào ?
a) - 2. 5091 = - 10 182 và 3. 5091 = 15 273
⇒ - 10 182 < 15 273
b) Nhân cả 2 vế của bất đẳng thức -2 < 3 với số c dương thì ta được bất đẳng thức: -2c < 3c
III. Bài tập vận dụng
Bài 1
a) Hãy cho biết vế trái, vế phải của bất phương trình x2 ≤ 6x –5
b) Chứng tỏ các số 3; 4 và 5 đều là nghiệm, còn số 6 không phải là nghiệm của bất phương trình vừa nêu.
Bài 2 Hãy cho biết vế trái, vế phải và tập nghiệm của bất phương trình x > 3, bất phương trình 3 < x và phương trình x = 3.
Bài 3 Viết và biểu diễn tập nghiệm của bất phương trình x ≥ -2 trên trục số.
Bài 4 Viết và biểu diễn tập nghiệm của bất phương trình x < 4 trên trục số.
Bài 5 Kiểm tra xem giá trị x = 3 là nghiệm của bất phương trình nào trong các bất phương trình sau:
a) 2x + 3 < 9
b) -4x > 2x + 5
c) 5 - x > 3x - 12
Bài 6 Viết và biểu diễn tập nghiệm trên trục số của mỗi bất phương trình sau:
a) x < 4 ; b) x ≤ -2
c) x > -3 ; d) x ≥ 1
Bài 7 Hình vẽ sau đây biểu diễn tập nghiệm của bất phương trình nào? (Chỉ nêu một bất phương trình).
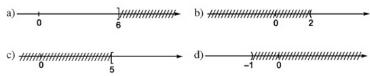
Bài 8 Hãy lập bất phương trình cho bài toán sau:
Bài 9 Quãng đường từ A đến B dài 50km. Một ô tô đi từ A đến B, khởi hành lúc 7h. Hỏi ô tô phải đi với vận tốc bao nhiêu km/h để đến B trước 9 giờ cùng ngày?
Bài 10 Viết và biểu diễn tập nghiệm trên trục số của mỗi bất phương trình sau:
a)
b)
c)
d)
Bài 11 Hãy lập bất phương trình cho bài toán sau:
Quãng đường đi từ A đến B dài 50km. Một ô tô đi từ A đến B, khởi hành lúc 7 giờ. Hỏi ô tô phải đi với vận tốc bao nhiêu km/h để đến B trước 9 giờ cùng ngày?
Bài tập Phương trình chứa dấu giá trị tuyệt đối - Toán 8
I. Bài tập trắc nghiệm
Bài 1: Biểu thức A = | 4x | + 2x - 1 với x < 0, rút gọn được kết quả là?
A. A = 6x - 1
B. A = 1 - 2x
C. A = - 1 - 2x
D. A = 1 - 6x
Ta có: x < 0 ⇒ | 4x | = - 4x
Khi đó ta có: A = | 4x | + 2x - 1 = - 4x + 2x - 1 = - 2x - 1
Chọn đáp án C.
Bài 2: Tập nghiệm của phương trình: | 3x + 1 | = 5
A. S = { - 2 }
B. S = { }
C. S = { - 2; }
D. S = { Ø }
Ta có: | 3x + 1 | = 5 ⇔
Vậy tập nghiệm của phương trình đã cho là S = { - 2; }
Chọn đáp án C.
Bài 3: Tập nghiệm của phương trình |2 - 3x| = |5 - 2x| là?
A. S = { - 3;1 }
B. S = { - 3; }
C. S = { 0; }
D. S = { - 3;1 }
Ta có: |2 - 3x| = |5 - 2x| ⇔
Vậy tập nghiệm của phương trình là S = { - 3; }
Chọn đáp án B.
Bài 4: Giá trị m để phương trình | 3 + x | = m có nghiệm x = - 1 là?
A. m = 2
B. m = - 2
C. m = 1
D. m = - 1
Phương trình đã cho có nghiệm x = - 1 nên ta có: | 3 + ( - 1 ) | = m ⇔ m = 2.
Vậy m = 2 là giá trị cần tìm.
Chọn đáp án A.
Bài 5: Giá trị của m để phương trình | x - m | = 2 có nghiệm là x = 1 ?
A. m ∈ { 1 }
B. m ∈ { - 1;3 }
C. m ∈ { - 1;0 }
D. m ∈ { 1;2 }
Phương trình có nghiệm x = 1, khi đó ta có:
| 1 - m | = 2 ⇔
Vậy giá trị m cần tìm là m ∈ { - 1;3 }
Chọn đáp án B.
Bài 6: Rút gọn biểu thức A = |2x + 4| + 2(x - 3) với x > 0
A. 4x - 2 B. 3 – 4x C. -10 D. 4x -10
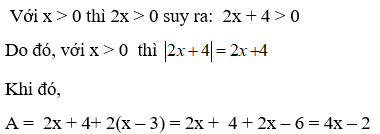
Chọn đáp án A
Bài 7: Với x > 2 thì |3 - (2x - 1)| bằng ?
A. 2x + 4 B. 2x - 4 C. 2x - 1 D. 2x – 2
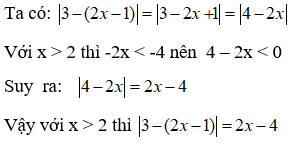
Bài 8: Tìm tất cả các giá trị của x thỏa mãn: |6 - 2(x + 2)| = 2 - 2x
A. x = 1 B. x < 1 C. x ≤ 1 D. x > 1
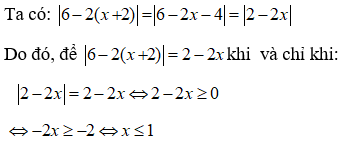
Chọn đáp án C
Bài 9: Giải phương trình sau: |x + 1| = 2x + 7
A. x = 8 hoặc x = -2
B. x = 2
C. x = 2 hoặc x = 8
D. x = 8
Lời giải:
Ta có: |x + 1| = x + 1 nếu x ≥ -1 Và |x + 1| = -x - 1 nếu x < -1
Để giải phương trình đã cho ta quy về giải hai phương trình sau:
* Phương trình x + 1 = 2x -7 với ⇔ -x = - 7 -1 ⇔ - x = -8 ⇔ x = 8 (thỏa mãn điều kiện )
* Phương trình –x – 1= 2x – 7 với x < -1
⇔ -x - 2x = -7 + 1
⇔ - 3x = - 6
⇔ x = 2 ( không thỏa mãn điều kiện x < -1)
Vậy nghiệm của phương trình đã cho là x = 8
Bài 10: Giải phương trình |2 - (x + 4)| = |2x - 3(x + 2)|
A. x = 3 hoặc x = -4
B. x = 1 hoặc x = -2
C. x = -4
D. x = 4 và x = 2
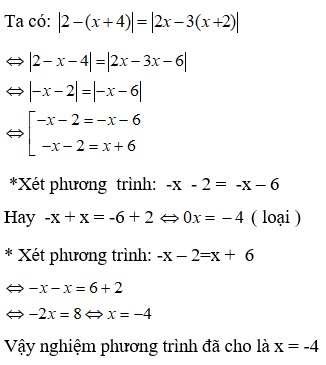
Chọn đáp án C
II. Bài tập tự luận có giải
Bài 1: Cho các khẳng định sau:
(1) |x – 3| = 1 chỉ có một nghiệm là x = 2
(2) x = 4 là nghiệm của phương trình |x – 3| = 1
(3) |x – 3| = 1 có hai nghiệm là x = 2 và x = 4
Các khẳng định đúng là?
Lời giải
Xét phương trình |x – 3| = 1
TH1: |x – 3| = x – 3 khi x – 3 ≥ 0 ⇔ x ≥ 3
Phương trình đã cho trở thành x – 3 = 1 ⇔ x = 4 (TM)
TH2: |x – 3| = 3 – x khi x – 3 < 0 ⇔ x < 3
Phương trình đã cho trở thành 3 – x = 1 ⇔ x = 2 (TM)
Vậy phương trình |x – 3| = 1 có hai nghiệm x = 2 và x = 4
Nên x = 4 là nghiệm của phương trình |x – 3| = 1
Khẳng định đúng là (2) và (3)
Bài 2: Cho các khẳng định sau:
(1) Phương trình |x – 3| = 1 chỉ có một nghiệm là x = 2
(2) Phương trình |x – 1| = 0 có 2 nghiệm phân biệt
(3) Phương trình |x – 3| = 1 có hai nghiệm phân biệt là x = 2 và x = 4
Số khẳng định đúng là?
Lời giải
Xét phương trình |x – 3| = 1
TH1: |x – 3| = x – 3 khi x – 3 ≥ 0 ⇔ x ≥ 3
Phương trình đã cho trở thành x – 3 = 1 ⇔ x = 4 (TM)
TH2: |x – 3| = 3 – x khi x – 3 < 0 ⇔ x < 3
Phương trình đã cho trở thanh 3 – x = 1 ⇔ x = 2 (TM)
Vậy phương trình |x – 3| = 1 có hai nghiệm x = 2 và x = 4 hay (1) sai và (3) đúng
|x – 1| = 0 ⇔ x – 1 = 0 ⇔ x = 1 nên phương trình |x – 1| = 0 có nghiệm duy nhất hay (2) sai.
Vậy có 1 khẳng định đúng
Bài 3: Nghiệm nhỏ nhất của phương trình |2 + 3x| = |4x – 3| là
Lời giải
Ta có |2 + 3x| = |4x – 3|
Vậy nghiệm nhỏ nhất của phương trình là x =
Bài 4 Nghiệm nhỏ nhất của phương trình |5 – 2x| = |x – 1| là?
Lời giải
Ta có |5 – 2x| = |x – 1|
Vậy nghiệm nhỏ nhất của phương trình là x = 2
Bài 5 Tổng các nghiệm của phương trình |3x – 1| = x + 4 là?
Lời giải
TH1: |3x – 1| = 3x – 1 khi |3x – 1| ≥ 0 ⇔ 3x ≥ 1 ⇔ x ≥
Phương trình đã cho trở thành 3x – 1 = x + 4
⇔ 2x = 5 ⇔ x = 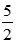
TH2: |3x – 1| = 1 – 3x khi 3x – 1 < 0 ⇔ x <
Phương trình đã cho trở thành 1 – 3x = x + 4
Bài 6 Rút gọn các biểu thức:
a) C = |-3x| + 7x – 4 khi x ≤ 0;
b) D = 5 – 4x + |x - 6| khi x < 6.
Lời giải
a) x ≤ 0 nên – 3x ≥ 0 ⇒ |-3x| = -3x
Vậy C = |-3x| + 7x – 4 = -3x + 7x - 4 = 4x - 4
b) x < 6 nên x – 6 < 0 ⇒ |x - 6| = -(x - 6) = 6 - x
Vậy D = 5 – 4x + |x - 6| = 5 – 4x + 6 – x = 11 – 5x
Bài 7 Giải các phương trình:
a) |x + 5| = 3x + 1;
b) |-5x| = 2x + 21.
Lời giải
a) Với x ≥ -5 thì x + 5 ≥ 0 nên |x + 5| = x + 5
x + 5 = 3x + 1 ⇔ 2x = 4 ⇔ x = 2 (thỏa mãn điều kiện x ≥ -5)
Với x < -5 thì x + 5 < 0 nên |x + 5| = - (x + 5) = - x - 5
-x - 5 = 3x + 1 ⇔ 4x = -6 ⇔ x = (không thỏa mãn điều kiện x ≤ -5)
Vậy tập nghiệm của bất phương trình |x + 5| = 3x + 1 là S = {2}
a) Với x ≥ 0 thì - 5x ≤ 0 nên |-5x| = -(-5x) = 5x
|-5x|= 2x + 21 ⇔ 5x = 2x + 21
⇔ 3x = 21 ⇔ x = 7 (không thỏa mãn điều kiện x ≥0)
Với x < 0 thì – 5x > 0 nên |-5x| = -5x
|-5x|= 2x + 21 ⇔ -5x = 2x + 21
⇔ -7x = 21 ⇔ x = -3 (thỏa mãn điều kiện x < 0)
Vậy tập nghiệm của bất phương trình |-5x|= 2x + 21 là S = {-3}
Bài 8 Bỏ dấu giá trị tuyệt đối và rút gọn các biểu thức:
a) A = 3x + 2 + |5x| trong hai trường hợp: x ≥ 0 và x < 0;
b) B = |-4x| - 2x + 12 trong hai trường hợp: x ≤ 0 và x > 0;
c) C = |x - 4| - 2x + 12 khi x > 5;
d) D = 3x + 2 + |x + 5|.
Ghi nhớ
(Trước khi đi vào lời giải, bạn cần ghi nhớ: Trị tuyệt đối của một số không âm bằng chính nó; Trị tuyệt đối của một số âm bằng số đối của nó.
Ví dụ:
|5x| = 5x khi x ≥ 0
|5x| = -5x khi x < 0)
Lời giải:
(Bài dưới được trình bày dựa theo cách trình bày ở Ví dụ 1 trang 50 sgk Toán 8 Tập 2. Bạn có thể rút gọn nếu bạn thích.)
a) - Khi x ≥ 0 ta có 5x ≥ 0 nên |5x| = 5x
Vậy A = 3x + 2 + 5x = 8x + 2
- Khi x < 0 ta có 5x < 0 nên |5x| = -5x
Vậy A = 3x + 2 - 5x = -2x + 2
b) - Khi x ≤ 0 ta có -4x ≥ 0 (nhân hai vế với số âm) nên |-4x| = -4x
Vậy B = -4x - 2x + 12 = -6x + 12
- Khi x > 0 ta có -4x < 0 nên |-4x| = -(-4x) = 4x
Vậy B = 4x - 2x + 12 = 2x + 12
c) - Khi x > 5 ta có x - 4 > 1 (trừ hai vế cho 4) hay x - 4 > 0 nên |x - 4| = x - 4
Vậy C = x - 4 - 2x + 12 = -x + 8
d) D = 3x + 2 + x + 5 khi x + 5 ≥ 0
hoặc D = 3x + 2 - (x + 5) khi x + 5 < 0
Vậy D = 4x + 7 khi x ≥ -5
hoặc D = 2x - 3 khi x < -5
Bài 9 Giải các phương trình:
a) |2x| = x - 6 ; b) |-3x| = x - 8
c) |4x| = 2x + 12 ; d) |-5x| - 16 = 3x
Lời giải:
a) |2x| = x – 6 (1)
Ta có: |2x| = 2x khi 2x ≥ 0 hay x ≥ 0
|2x| = -2x khi 2x < 0 hay x < 0.
Vậy phương trình (1) tương đương với:
+ 2x = x – 6 với điều kiện x ≥ 0
2x = x – 6 ⇔ x = -6
Giá trị x = -6 không thỏa mãn điều kiện x ≥ 0 nên không phải nghiệm của (1)
+ -2x = x – 6 với điều kiện x < 0
-2x = x – 6 ⇔ -3x = -6 ⇔ x = 2.
Giá trị x = 2 không thỏa mãn điều kiện x < 0 nên không phải nghiệm của (1).
Vậy phương trình (1) vô nghiệm.
b) |-3x| = x – 8 (2)
Ta có: |-3x| = -3x khi -3x ≥ 0 hay x ≤ 0.
|-3x| = -(-3x) = 3x khi -3x < 0 hay x > 0.
Vậy phương trình (2) tương đương với:
+ -3x = x – 8 với điều kiện x ≤ 0
-3x = x – 8 ⇔ -4x = -8 ⇔ x = 2
Giá trị x = 2 không thỏa mãn điều kiện x ≤ 0 nên không phải nghiệm của (2).
+ 3x = x – 8 với điều kiện x > 0
3x = x – 8 ⇔ 2x = -8 ⇔ x = -4.
Giá trị x = -4 không thỏa mãn điều kiện x > 0 nên không phải nghiệm của (2).
Vậy phương trình (2) vô nghiệm.
c) |4x| = 2x + 12 (3)
Ta có: |4x| = 4x khi 4x ≥ 0 ⇔ x ≥ 0
|4x| = -4x khi 4x < 0 hay x < 0.
Vậy phương trình (3) tương đương với:
+ 4x = 2x + 12 với điều kiện x ≥ 0
4x = 2x + 12 ⇔ 2x = 12 ⇔ x = 6.
Giá trị x = 6 thỏa mãn điều kiện x ≥ 0 nên là nghiệm của (3)
+ -4x = 2x + 12 với điều kiện x < 0
-4x = 2x + 12 ⇔ -6x = 12 ⇔ x = -2.
Giá trị x = -2 thỏa mãn điều kiện x < 0 nên là nghiệm của (3).
Vậy phương trình (3) có hai nghiệm x = 6 và x = -2.
d) |-5x| - 16 = 3x (4)
Ta có: |-5x| = -5x khi -5x ≥ 0 hay x ≤ 0.
|-5x| = -(-5x) = 5x khi -5x < 0 hay x > 0.
Vậy phương trình (4) tương đương với:
+ -5x – 16 = 3x với điều kiện x ≤ 0.
-5x – 16 = 3x ⇔ -5x – 3x = 16 ⇔ -8x = 16 ⇔ x = -2.
Giá trị x = -2 thỏa mãn điều kiện x ≤ 0 nên là nghiệm của (4).
+ 5x – 16 = 3x với điều kiện x > 0.
5x – 16 = 3x ⇔ 5x – 3x = 16 ⇔ 2x = 16 ⇔ x = 8
Giá trị x = 8 thỏa mãn điều kiện x > 0 nên là nghiệm của (4).
Vậy phương trình (4) có nghiệm x = -2 và x = 8.
Bài 10 Giải các phương trình:
a) |x - 7| = 2x + 3; b) |x + 4| = 2x - 5
c) |x+ 3| = 3x - 1; d) |x - 4| + 3x = 5
Lời giải:
a) |x – 7| = 2x + 3 (1)
Ta có: |x – 7| = x – 7 khi x – 7 ≥ 0 hay x ≥ 7.
|x – 7| = -(x – 7) = 7 – x khi x – 7 < 0 hay x < 7.
Vậy phương trình (1) tương đương với:
+ x – 7 = 2x + 3 khi x ≥ 7
x – 7 = 2x + 3 ⇔ x = -10.
Giá trị x = -10 không thỏa mãn điều kiện x ≥ 7 nên không phải nghiệm của (1).
+ 7 – x = 2x + 3 khi x < 7.
7 – x = 2x + 3 ⇔ 3x = 4 ⇔ x =
Giá trị x = thỏa mãn điều kiện x < 7 nên là nghiệm của (1)
Vậy phương trình (1) có nghiệm x = .
b) |x + 4| = 2x – 5 (2)
Ta có: |x + 4| = x + 4 khi x + 4 ≥ 0 hay x ≥ -4.
|x + 4| = -(x + 4) = -x – 4 khi x + 4 < 0 hay x < -4.
Vậy phương trình (1) tương đương với:
+ x + 4 = 2x – 5 khi x ≥ -4
x + 4 = 2x – 5 ⇔ x = 9
Giá trị x = 9 thỏa mãn điều kiện x ≥ -4 nên là nghiệm của (2).
+ -x – 4 = 2x – 5 khi x < -4.
– x – 4 = 2x – 5 ⇔ 3x = 1 ⇔ x =
Giá trị x = không thỏa mãn điều kiện x < -4 nên không phải nghiệm của (2)
Vậy phương trình (2) có nghiệm x = 9.

Vậy phương trình có nghiệm
III. Bài tập vận dụng
Bài 1 Giải các phương trình:
a)
b)
c)
d)
Bài 2 Bỏ dấu giá trị tuyệt đối và rút gọn các biểu thức:
a) trong hai trường hợp và
b) trong hai trường hợp và
c) khi
d)
Bài 3 Giải các phương trình:
a)
b)
c)
d)
Bài 4 Cho chứng minh:
a)
b)
c)
d)
Bài 5 Kiểm tra xem -2 là nghiệm của bất phương trình nào trong các bất phương trình sau:
a)
b)
c)
d)
e)
f)
Bài 6 Giải các bất phương trình và biểu diễn tập nghiệm trên trục số:
a)
b)
c)
d)
Bài 7 Giải các bất phương trình:
a)
b)
c)
d)
Bài 8 Giải các bất phương trình:
a)
b)
c)
d)
Bài 9 Tìm x sao cho:
a) Giá trị của biểu thức là số dương
b) Giá trị của biểu thức nhỏ hơn giá trị của biểu thức
c) Giá trị của biểu thức không nhỏ hơn giá trị của biểu thức
d) Giá trị của biểu thức không lớn hơn giá trị của biểu thức
Bài 10 Trong một cuộc thi đố vui. Ban tổ chức quy định mỗi người dự thi phải trả lời 10 câu hỏi ở vòng sơ tuyển. Mỗi câu hỏi này có sẵn 4 đáp án, nhưng trong đó chỉ có 1 đáp án đúng. Người dự thi chọn đáp án đúng sẽ được 5 điểm, chọn đáp án sai sẽ bị trừ đi 1 điểm. Ở vòng sơ tuyển, Ban tổ chức tặng cho mỗi người dự thi 10 điểm và quy định người nào có tổng số điểm từ 40 trở lên mới được dự thi ở vòng tiếp theo. Hỏi người dự thi phải trả lời chính xác bao nhiêu câu hỏi ở vong sơ tuyển thì mới được dự thi tiếp ở vòng sau?
Bài 11 Giải các phương trình:
a)
b)
c)
d)
Xem thêm các bộ đề thi Toán lớp 8 chọn lọc, hay khác:
Hệ thống kiến thức Toán lớp 8 Giữa học kì 2
TOP 30 Đề thi Học kì 2 Toán lớp 8 năm 2023 có đáp án
Bộ đề thi Toán lớp 8 Học kì 2 năm 2023 tải nhiều nhất (30 đề)