Trắc nghiệm Tích vô hướng của hai vectơ có đáp án (Thông hiểu)
Trắc nghiệm Tích vô hướng của hai vectơ có đáp án (Thông hiểu)
-
332 lượt thi
-
15 câu hỏi
-
20 phút
Danh sách câu hỏi
Câu 1:
23/07/2024Trong mặt phẳng cho 2 vec tơ và . Kết luận nào sau đây sai?
 Xem đáp án
Xem đáp án
Đáp án C
Phương án A: nên loại A
Phương án B: suy ra nên loại B
Phương án C: nên chọn C
Câu 3:
19/07/2024Trong mặt phẳng tọa độ Oxy, cho ba điểm . Tính cosin góc giữa hai vec tơ và
 Xem đáp án
Xem đáp án
Đáp án D
Ta có:
Suy ra
Câu 4:
16/07/2024Cho tam giác ABC vuông tại A và có AB = c, AC = b. Tính
 Xem đáp án
Xem đáp án
Đáp án B
Ta có:
Cách khác:
Tam giác ABC vuông tại A suy ra
Ta có:
Câu 5:
02/12/2024Cho hình vuông ABCD cạnh a. Gọi E là điểm đối xứng của D qua C. Tính
 Xem đáp án
Xem đáp án
Đáp án đúng: A
*Lời giải:
Ta có C là trung điểm của DE nên DE = 2a
Khi đó
*Phương pháp giải:
Áp dụng tính chất về tích vô hướng của hai vectơ để làm
* Lý thuyết nắm thêm về tích vô hướng của hai vectơ:
Hai vectơ cùng phương, cùng hướng, bằng nhau.
+ Đường thẳng đi qua điểm đầu và điểm cuối của một vectơ được gọi là giá của vectơ đó.
+ Hai vectơ được gọi là cùng phương nếu chúng có giá song song hoặc trùng nhau.
+ Đối với hai vectơ cùng phương thì chúng cùng hướng hoặc ngược hướng.
+ Hai vectơ và được gọi là bằng nhau, kí hiệu là = , nếu chúng có cùng độ dài và cùng hướng.
Ví dụ:

Trong hình trên đường thẳng m đi qua điểm đầu và điểm cuối của vectơ , nên đường thẳng m gọi là giá của vectơ .
Tương tự, đường thẳng n là giá của hai vectơ và .
Đường thẳng m và n song song với nhau nên ba vectơ và và là các vectơ cùng phương.
và cùng phương nhưng ngược hướng; và cùng phương và cùng hướng.
Hai vectơ và cùng hướng, ngoài ra chúng có độ dài bằng nhau nên = .
Chú ý:
+ Ta cũng xét các vectơ điểm đầu và điểm cuối trùng nhau (chẳng hạn , ), gọi là các vectơ–không.
+ Ta quy ước vectơ–không có độ dài bằng 0, cùng hướng (do đó cùng phương) với mọi vectơ.
+ Các vectơ–không có cùng độ dài và cùng hướng nên bằng nhau và được kí hiệu chung là .
+ Với mỗi điểm O và vectơ cho trước, có duy nhất điểm A sao cho .
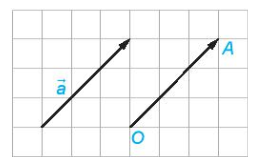
Nhận xét: Ba điểm phân biệt A, B, C thẳng hàng khi và chỉ khi và cùng phương.

Chú ý: Ta có thể dùng vectơ để biểu diễn các đại lượng như lực, vận tốc, gia tốc. Hướng của vectơ chỉ hướng của đại lượng, độ dài của vectơ thể hiện cho độ lớn của đại lượng và được lấy tỉ lệ với độ lớn của đại lượng.
Xem thêm các bài viết liên quan hay, chi tiết:
Lý thuyết Toán 10 Bài 7: Các khái niệm mở đầu - Kết nối tri thức
Câu 6:
18/07/2024Cho hình vuông ABCD cạnh a. Hỏi mệnh đề nào sau đây sai?
 Xem đáp án
Xem đáp án
Đáp án C
Phương án A: Do nên A đúng, loại A.
Phương án B: Do nên B đúng, loại B.
Phương án C: nên C sai, chọn C.
Phương án D: đúng vì AB⊥AD, CB⊥CD
Câu 7:
22/07/2024Cho hình thang vuông ABCD có đáy lớn AB = 4a, đáy nhỏ CD = 2a, đường cao AD = 3a; I là trung điểm của AD. Câu nào sau đây sai?
 Xem đáp án
Xem đáp án
Đáp án D
Phương án A: nên loại A
Phương án B: suy ra nên loại B
Phương án C: suy ra nên loại C
Phương án D: không vuông góc với suy ra nên chọn D
Câu 9:
21/07/2024Cho tam giác ABC vuông cân tại A và có AB = AC = a. Tính
 Xem đáp án
Xem đáp án
Đáp án A
Xác định được góc là góc ngoài của góc nên
Do đó
Câu 10:
12/07/2024Cho hai vec tơ và đều có độ dài bằng 1 thỏa mãn . Hãy xác định
 Xem đáp án
Xem đáp án
Đáp án C
Câu 11:
19/07/2024Trong mặt phẳng tọa độ Oxy, cho hai vec tơ và . Tìm k để vec tơ
 Xem đáp án
Xem đáp án
Đáp án C
Từ giả thiết suy ra
Yêu cầu bài toán
Câu 12:
19/07/2024Cho M là trung điểm AB, tìm biểu thức sai:
 Xem đáp án
Xem đáp án
Đáp án D
Phương án A: ngược hướng suy ra
nên loại A
Phương án B: ngược hướng suy ra
nên loại B
Phương án C: cùng hướng suy ra
nên loại C
Phương án D: ngược hướng suy ra
nên chọn D
Câu 13:
22/07/2024Cho hình vuông ABCD tâm O. Hỏi mệnh đề nào sau đây sai?
 Xem đáp án
Xem đáp án
Đáp án C
Phương án A: suy ra nên loại A
Phương án B: nên loại B
Phương án C:
nên chọn C
Câu 14:
15/07/2024Cho tam giác đều ABC cạnh a, với đường cao BK. Câu nào sau đây đúng?
 Xem đáp án
Xem đáp án
Đáp án C
Phương án A: do
nên loại A
Phương án B: do nên loại B và loại D
Phương án C: do nên chọn C
Câu 15:
28/11/2024Cho hình vuông ABCD, tính
 Xem đáp án
Xem đáp án
Đáp án đúng là D
Lời giải
*Phương pháp giải:
*Lý thuyết:
- Cho hai vectơ và đều khác vectơ ta có:
( )
- Cho hai vectơ và đều khác vectơ ta có:
- Lưu ý: Góc giữa hai vectơ luôn có số đo từ đến .
Xem thêm
Có thể bạn quan tâm
- Trắc nghiệm Tích vô hướng của hai vectơ (có đáp án) (355 lượt thi)
- Trắc nghiệm: Tích vô hướng của hai vectơ có đáp án (480 lượt thi)
- Trắc nghiệm Tích vô hướng của hai vectơ có đáp án (Nhận biết) (366 lượt thi)
- Trắc nghiệm Tích vô hướng của hai vectơ có đáp án (Thông hiểu) (331 lượt thi)
- Trắc nghiệm Tích vô hướng của hai vectơ có đáp án (Vận dụng) (224 lượt thi)
- Trắc nghiệm Tích vô hướng của hai vectơ có đáp án (Tổng hợp) (360 lượt thi)
Các bài thi hot trong chương
- Trắc nghiệm Các hệ thức lượng trong tam giác và giải tam giác (có đáp án) (2930 lượt thi)
- Trắc nghiệm Giá trị lượng giác của một góc bất kì từ 0 độ đến 180 độ (có đáp án) (2544 lượt thi)
- 100 câu trắc nghiệm Tích vô hướng của hai vectơ nâng cao (1194 lượt thi)
- 100 câu trắc nghiệm Tích vô hướng của hai vectơ cơ bản (1150 lượt thi)
- Trắc nghiệm Hình học Ôn tập chương 2 (có đáp án) (836 lượt thi)
- Trắc nghiệm: Giá trị lượng giác của một góc bất kì 0° đến 180° (536 lượt thi)
- Trắc nghiệm Giá trị lượng giác của một góc bất kì từ 0o đến 150o có đáp án (Nhận biết) (535 lượt thi)
- Trắc nghiệm Giá trị lượng giác của một góc bất kì từ 0o đến 150o có đáp án (Vận dụng) (507 lượt thi)
- Trắc nghiệm: Hệ thức lượng trong tam giác có đáp án (459 lượt thi)
- Trắc nghiệm Các hệ thức lượng trong tam giác và giải tam giác có đáp án (Nhận biết) (416 lượt thi)
