Cho hình vuông ABCD cạnh a. Gọi E là điểm đối xứng của D qua C. Tính $\overrightarrow{AE}.\overrightarrow{AB}$

Đáp án đúng: A

*Lời giải:

Ta có C là trung điểm của DE nên DE = 2a

Khi đó

$$\begin{gathered} \overrightarrow{AE}.\overrightarrow{AB}=\left(\overrightarrow{AD}+\overrightarrow{DE}\right).\overrightarrow{AB} \\ =\underset{0}{\underbrace{\overrightarrow{AD}.\overrightarrow{AB}}}+\overrightarrow{DE}.\overrightarrow{AB} \\ =DE.AB.\cos \left(\overrightarrow{DE},\overrightarrow{AB}\right) \\ =DE.AB.\cos 0^0=2a^2 \end{gathered}$$

*Phương pháp giải:

Áp dụng tính chất về tích vô hướng của hai vectơ để làm

* Lý thuyết nắm thêm về tích vô hướng của hai vectơ:

Hai vectơ cùng phương, cùng hướng, bằng nhau.

+ Đường thẳng đi qua điểm đầu và điểm cuối của một vectơ được gọi là giá của vectơ đó.

+ Hai vectơ được gọi là cùng phương nếu chúng có giá song song hoặc trùng nhau.

+ Đối với hai vectơ cùng phương thì chúng cùng hướng hoặc ngược hướng.

+ Hai vectơ  và  được gọi là bằng nhau, kí hiệu là $\overrightarrow{a}$  = $\overrightarrow{b}$ , nếu chúng có cùng độ dài và cùng hướng.

Ví dụ:

Trong hình trên đường thẳng m đi qua điểm đầu và điểm cuối của vectơ $\overrightarrow{a}$, nên đường thẳng m gọi là giá của vectơ $\overrightarrow{a}$ .

Tương tự, đường thẳng n là giá của hai vectơ $\overrightarrow{b}$  và $\overrightarrow{c}$ .

Đường thẳng m và n song song với nhau nên ba vectơ $\overrightarrow{a}$  và $\overrightarrow{b}$  và $\overrightarrow{c}$   là các vectơ cùng phương.

$\overrightarrow{a}$ và $\overrightarrow{b}$  cùng phương nhưng ngược hướng; $\overrightarrow{a}$  và $\overrightarrow{c}$  cùng phương và cùng hướng.

Hai vectơ $\overrightarrow{a}$  và $\overrightarrow{c}$  cùng hướng, ngoài ra chúng có độ dài bằng nhau nên $\overrightarrow{a}$  = $\overrightarrow{c}$ .

Chú ý:

+ Ta cũng xét các vectơ điểm đầu và điểm cuối trùng nhau (chẳng hạn $\overrightarrow{AA}$ , $\overrightarrow{BB}$ ), gọi là các vectơ–không.

+ Ta quy ước vectơ–không có độ dài bằng 0, cùng hướng (do đó cùng phương) với mọi vectơ.

+ Các vectơ–không có cùng độ dài và cùng hướng nên bằng nhau và được kí hiệu chung là $\overrightarrow{0}$ .

+ Với mỗi điểm O và vectơ $\overrightarrow{a}$  cho trước, có duy nhất điểm A sao cho $\overrightarrow{OA}=\overrightarrow{a}$ .

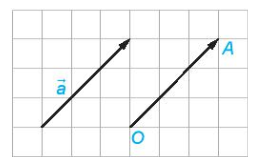
Nhận xét: Ba điểm phân biệt A, B, C thẳng hàng khi và chỉ khi $\overrightarrow{AB}$  và $\overrightarrow{AC}$ cùng phương.

Chú ý: Ta có thể dùng vectơ để biểu diễn các đại lượng như lực, vận tốc, gia tốc. Hướng của vectơ chỉ hướng của đại lượng, độ dài của vectơ thể hiện cho độ lớn của đại lượng và được lấy tỉ lệ với độ lớn của đại lượng.

Xem thêm các bài viết liên quan hay, chi tiết:

Lý thuyết Toán 10 Bài 7: Các khái niệm mở đầu - Kết nối tri thức

Giải Toán 10 Bài 7 (Kết nối tri thức): Các khái niệm mở đầu