Trắc nghiệm Toán 12 Bài 2: Cực trị hàm số
-
841 lượt thi
-
30 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
02/12/2024Tìm giá trị cực đại yCĐ của hàm số y = x3 - 3x +2
 Xem đáp án
Xem đáp án
Đáp án đúng A.
*Lời giải:
Ta có
*Phương pháp giải:
Tính y'
Tìm nghiệm y' thay vào y để tìm yCĐ
* Lý thuyết nắm thêm về cực trị hàm số:
- Định nghĩa.
Cho hàm số y = f(x) xác định và liên tục trên khoảng (a; b) (có thể a là ; b là ) và điểm x0(a; b).
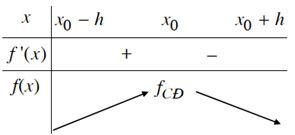
a) Nếu tồn tại số h > 0 sao cho f(x) < f(x0) với mọi x(x0 – h; x0 + h) và thì ta nói hàm số f(x) đạt cực đại tại x0.
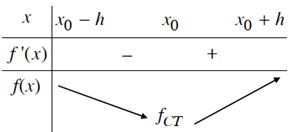
b) Nếu tồn tại số h > 0 sao cho f(x) > f(x0) với mọi x(x0 – h; x0 + h) và thì ta nói hàm số f(x) đạt cực tiểu tại x0.
- Chú ý:
1. Nếu hàm số f(x) đạt cực đại (cực tiểu) tại x0 thì x0 được gọi là điểm cực đại (điểm cực tiểu) của hàm số; f(x0) được gọi là giá trị cực đại (giá trị cực tiểu) của hàm số.
Kí hiệu là fCĐ (fCT) còn điểm M(x0; f(x0)) được gọi là điểm cực đại (điểm cực tiểu) của đồ thị hàm số.
2. Các điểm cực đại, cực tiểu được gọi chung là điểm cực trị. Giá trị cực đại (giá trị cực tiểu) còn gọi là cực đại (cực tiểu) và được gọi chung là cực trị của hàm số.
3. Dễ dàng chứng minh được rằng, nếu hàm số y = f(x) có đạo hàm trên khoảng (a; b) và đạt cực đại hoặc cực tiểu tại x0 thì f’(x0) = 0.
II. Điều kiện đủ để hàm số có cực trị
- Định lí 1
Giả sử hàm số y = f(x) liên tục trên khoảng K = (x0 – h; x0 + h) và có đạo hàm trên K hoặc trên K \ {x0}; với h > 0.
a) Nếu f’(x) > 0 trên khoảng (x0 – h; x0) và f’(x) < 0 trên khoảng (x0; x0 + h) thì x0 là một điểm cực đại của hàm số f(x).
b) Nếu f’(x) < 0 trên khoảng (x0 – h; x0) và f’(x) > 0 trên khoảng (x0; x0 + h) thì x0 là một điểm cực tiểu của hàm số f(x).
Xem thêm các bài viết liên quan hay, chi tiết:
Câu 2:
27/11/2024Cho hàm số . Mệnh đề nào dưới đây đúng?
 Xem đáp án
Xem đáp án
Đáp án đúng là D
Lời giải
Ta có:
*Phương pháp giải:
1.Tính đạo hàm và giải tìm nghiệm
2. lấy nghiệm tìm được thay vào y dể tìm cực tiểu
*Lý thuyết:
- Định nghĩa.
Cho hàm số y = f(x) xác định và liên tục trên khoảng (a; b) (có thể a là ; b là ) và điểm x0(a; b).
a) Nếu tồn tại số h > 0 sao cho f(x) < f(x0) với mọi x(x0 – h; x0 + h) và thì ta nói hàm số f(x) đạt cực đại tại x0.
b) Nếu tồn tại số h > 0 sao cho f(x) > f(x0) với mọi x(x0 – h; x0 + h) và thì ta nói hàm số f(x) đạt cực tiểu tại x0.
- Chú ý:
1. Nếu hàm số f(x) đạt cực đại (cực tiểu) tại x0 thì x0 được gọi là điểm cực đại (điểm cực tiểu) của hàm số; f(x0) được gọi là giá trị cực đại (giá trị cực tiểu) của hàm số.
Kí hiệu là fCĐ (fCT) còn điểm M(x0; f(x0)) được gọi là điểm cực đại (điểm cực tiểu) của đồ thị hàm số.
2. Các điểm cực đại, cực tiểu được gọi chung là điểm cực trị. Giá trị cực đại (giá trị cực tiểu) còn gọi là cực đại (cực tiểu) và được gọi chung là cực trị của hàm số.
3. Dễ dàng chứng minh được rằng, nếu hàm số y = f(x) có đạo hàm trên khoảng (a; b) và đạt cực đại hoặc cực tiểu tại x0 thì f’(x0) = 0.
II. Điều kiện đủ để hàm số có cực trị
- Định lí 1
Giả sử hàm số y = f(x) liên tục trên khoảng K = (x0 – h; x0 + h) và có đạo hàm trên K hoặc trên K \ {x0}; với h > 0.
a) Nếu f’(x) > 0 trên khoảng (x0 – h; x0) và f’(x) < 0 trên khoảng (x0; x0 + h) thì x0 là một điểm cực đại của hàm số f(x).
b) Nếu f’(x) < 0 trên khoảng (x0 – h; x0) và f’(x) > 0 trên khoảng (x0; x0 + h) thì x0 là một điểm cực tiểu của hàm số f(x).


Xem thêm
Câu 3:
17/07/2024Đồ thị của hàm số y = x3 - 3x2 - 9x +1 có hai điểm cực trị A và B. Điểm nào dưới đây thuộc đường thẳng AB?
 Xem đáp án
Xem đáp án
Ta có:
Chọn C.
Câu 4:
23/07/2024Đồ thị của hàm số y = -x3 + 3x +5 có hai điểm cực trị A và B. Tính diện tích S của tam giác OAB với O là gốc tọa độ.
 Xem đáp án
Xem đáp án
Ta có:
Ta có:
Chọn C.
Câu 7:
15/07/2024Số điểm cực trị của hàm số y = x3+x2+3x-1 là
 Xem đáp án
Xem đáp án
Ta có y' = 3x2+2x+3>0 không có cực trị.
Chọn B.
Câu 8:
16/11/2024Tìm điểm cực tiểu của đồ thị hàm số y = x3 -3x2 -1?
 Xem đáp án
Xem đáp án
Đáp án đúng: D.
*Lời giải
*Phương pháp giải:
Tính y'
Tìm nghiệm y' thay nghiệm vào y tìm CĐ CT
*Lý thuyết cần nắm và các dạng bài tập về cực trị hàm số:
- Định nghĩa.
Cho hàm số y = f(x) xác định và liên tục trên khoảng (a; b) (có thể a là −∞; b là +∞) và điểm x0∈(a; b).
a) Nếu tồn tại số h > 0 sao cho f(x) < f(x0) với mọi x(x0 – h; x0 + h) và x≠x0 thì ta nói hàm số f(x) đạt cực đại tại x0.
b) Nếu tồn tại số h > 0 sao cho f(x) > f(x0) với mọi x∈(x0 – h; x0 + h) và x≠x0 thì ta nói hàm số f(x) đạt cực tiểu tại x0.
Điều kiện đủ để hàm số có cực trị
- Định lí 1
Giả sử hàm số y = f(x) liên tục trên khoảng K = (x0 – h; x0 + h) và có đạo hàm trên K hoặc trên K \ {x0}; với h > 0.
a) Nếu f’(x) > 0 trên khoảng (x0 – h; x0) và f’(x) < 0 trên khoảng (x0; x0 + h) thì x0 là một điểm cực đại của hàm số f(x).
b) Nếu f’(x) < 0 trên khoảng (x0 – h; x0) và f’(x) > 0 trên khoảng (x0; x0 + h) thì x0 là một điểm cực tiểu của hàm số f(x).


Quy tắc tìm cực trị.
- Quy tắc 1.
1. Tìm tập xác định.
2. Tính f’(x). Tìm các điểm tại đó f’(x) bằng 0 hoặc f’(x) không xác định.
3. Lập bảng biến thiên.
4. Từ bảng biến thiên suy ra các điểm cực trị.
- Định lí 2.
Giả sử hàm số y = f(x) có đạo hàm cấp hai trong khoảng (x0 – h; x0 + h) với h > 0. Khi đó:
a) Nếu f’(x0) = 0; f”(x0) > 0 thì x0 là điểm cực tiểu;
b) Nếu f’(x0) = 0; f”(x0) < 0 thì x0 là điểm cực đại.
- Quy tắc II.
1. Tìm tập xác định
2. Tính f’(x). Giải phương trình f’(x) = 0 và kí hiệu xi ( i = 1; 2; ….; n) là các nghiệm của nó.
3. Tính f”(x) và f”(xi).
4. Dựa vào dấu của f”(xi) suy ra tính chất cực trị của điểm xi.
Kỹ năng giải nhanh các bài toán cực trị hàm số bậc ba ().
- Ta có
Đồ thị hàm số có 2 điểm cực trị khi phương trình y' = 0 có hai nghiệm phân biệt .
Và không có cực trị ⇔Δ’ = b2 − 3ac ≤ 0
- Cho hàm số có hai điểm cực trị phân biệt là A, B . Khi đó:
Phương trình đường thẳng AB : y = (c - )x + (d -)
Độ dài đoạn thẳng AB = với e =
Hoặc khi đó đường thẳng qua hai điểm cực trị liên quan tới: (CASIO hỗ trợ).
Kỹ năng giải nhanh các bài toán cực trị hàm trùng phương.
Cho hàm số: () có đồ thị là (C) .
Ta có
(C) có ba điểm cực trị y' = 0 có 3 nghiệm phân biệt hay ab < 0
Hàm số có 3 cực trị là:
.
Độ dài các đoạn thẳng:
CÁC DẠNG BÀI TẬP THƯỜNG GẶP VÀ PHƯƠNG PHÁP GIẢI.
Dạng 1. Tìm các điểm cực trị của hàm số.
Quy tắc 1: Áp dụng định lý 2
- Tìm f’(x)
- Tìm các điểm xi (i = 1, 2, 3,…) tại đó đạo hàm bằng 0 hoặc hàm số liên tục nhưng không có đạo hàm
- Xét dấu của f’(x). Nếu f’(x) đổi dấu khi x qua điểm xo thì hàm số có cực trị tại điểm xo
Quy tắc 2: Áp dụng định lý 3
- Tìm f’(x)
- Tìm các nghiệm xi (i = 1, 2, 3,…) của phương trình f ‘(x) = 0
- Với mỗi xi tính f ”(xi)
- Nếu f ”(xi) < 0 thì hàm số đạt cực đại tại điểm xi
- Nếu f ”(xi) > 0 thì hàm số đạt cực tiểu tại điểm xi
Dạng 2: Tìm điều kiện để hàm số có cực trị.
Sử dụng định lí 2 và định lí 3
a, Cực trị của hàm số bậc ba:
Cho hàm số y = ax3 + bx2 + cx + d, a ≠ 0.
y’ = 0 ⇔ 3ax2 + 2bx + c = 0 (1) ; Δ’y’ = b2 – 3ac
- Phương trình (1) vô nghiệm hoặc có nghiệm kép thì hàm số đã cho không có cực trị.
→ Hàm số bậc 3 không có cực trị ⇔ b2 – 3ac ≤ 0
- Phương trình (1) có hai nghiệm phân biệt thì hàm số đã cho có 2 cực trị.
→ Hàm số bậc 3 có 2 cực trị ⇔ b2 – 3ac > 0
b, Cực trị của hàm số bậc bốn trùng phương:
Cho hàm số: y = ax4 + bx2 + c (a ≠ 0) có đồ thị là (C).
y' = 4ax3 + 2bx; y' = 0
⇔
- Nếu (C)có một điểm cực trị thì y' = 0 có 1 nghiệm x = 0 ⇔ -b/2a ≤ 0 ⇔ ab ≥ 0.
- Nếu (C)có ba điểm cực trị thì y' = 0 có 3 nghiệm phân biệt ⇔ -b/2a > 0 ⇔ ab < 0.
Chú ý
* Hàm số f (xác định trên D) có cực trị ⇔ ∃ xo ∈ D thỏa mãn hai điều kiện sau:
- Tại đạo hàm của hàm số tại xo phải bằng 0 hoặc hàm số không có đạo hàm tại xo
- f ‘(x) phải đổi dấu qua điểm xo hoặc f ”(xo) ≠ 0.
Xem thêm các bài viết liên quan hay, chi tiết
Lý thuyết Cực trị của hàm số (mới 2024 + Bài Tập) – Toán 12
Cực trị của hàm số và cách giải các dạng bài tập (2024) mới nhất
Câu 10:
09/10/2024Hàm số nào sau đây không có điểm cực trị
 Xem đáp án
Xem đáp án
Đáp án đúng: B
*Phương pháp giải:
- Nắm vững lại kiến thức cũng như điều kiện để xác định cực trị của một hàm số
*Lời giải:
Hàm số y = x3 không có cực trị.
* Lý thuyết thêm về cực trị hàm số:
+) Điều kiện cần để hàm số có cực trị.
Định lý 1: Giả sử hàm số f(x) đạt cực trị tại điểm xo. Khi đó, nếu f(x) có đạo hàm tại điểm xo thì f‘(xo) = 0.
+) Điều kiện đủ để hàm số có cực trị.
Định lý 2: Giả sử hàm số y = f(x) liên tục trên K = ( x0 -h: x0 +h ) và có đạo hàm trên K hoặc trên , với h >0 .
- Nếu f '(x) > 0 trên khoảng (x0 - h; x0) và trên thì x0 là một điểm cực đại của hàm số f(x) .
- Nếu f '(x) < 0 trên khoảng (x0 - h; x0) và f '(x) > 0 trên thì x0 là một điểm cực tiểu của hàm số f(x) .
Định lý 3: Giả sử hàm số f có đạo hàm cấp một trên khoảng (a; b) chứa điểm xo ; f ‘(xo) = 0 và f có đạo hàm cấp hai khác 0 tại điểm xo
a) Nếu f ”(xo) < 0 thì hàm số f đạt cực đại tại điểm xo
b) Nếu f ”(xo) < 0 thì hàm số f đạt cực tiểu tại điểm xo
* Dạng bài về cực trị hàm số:
a) Dạng 1. Tìm các điểm cực trị của hàm số.
* Phương pháp giải.
Quy tắc 1: Áp dụng định lý 2
- Tìm f’(x)
- Tìm các điểm xi (i = 1, 2, 3,…) tại đó đạo hàm bằng 0 hoặc hàm số liên tục nhưng không có đạo hàm
- Xét dấu của f’(x). Nếu f’(x) đổi dấu khi x qua điểm xo thì hàm số có cực trị tại điểm xo
Quy tắc 2: Áp dụng định lý 3
- Tìm f’(x)
- Tìm các nghiệm xi (i = 1, 2, 3,…) của phương trình f ‘(x) = 0
- Với mỗi xi tính f ”(xi)
- Nếu f ”(xi) < 0 thì hàm số đạt cực đại tại điểm xi
- Nếu f ”(xi) > 0 thì hàm số đạt cực tiểu tại điểm xi
b) Dạng 2: Tìm điều kiện để hàm số có cực trị.
* Phương pháp. Sử dụng định lí 2 và định lí 3
* Cực trị của hàm số bậc ba: Cho hàm số y = ax3 + bx2 + cx + d, a ≠ 0.
y’ = 0 ⇔ 3ax2 + 2bx + c = 0 (1) ; Δ’y’ = b2 – 3ac
- Phương trình (1) vô nghiệm hoặc có nghiệm kép thì hàm số đã cho không có cực trị.
→ Hàm số bậc 3 không có cực trị ⇔ b2 – 3ac ≤ 0
- Phương trình (1) có hai nghiệm phân biệt thì hàm số đã cho có 2 cực trị.
→ Hàm số bậc 3 có 2 cực trị ⇔ b2 – 3ac > 0
c) Dạng 3: Tìm điều kiện để các điểm cực trị của hàm số thỏa mãn điều kiện cho trước.
* Phương pháp giải: Hàm số bậc ba y = ax3 + bx2 + cx + d (a ≠ 0, a, b, c, d phụ thuộc vào tham số)
Bước 1: Tính y’ = 3ax2 + 2bx + c, y’ = 0 ⇔ 3ax2 +2bx + c = 0 (1)
Để hàm số có cực đại, cực tiểu ⇔ y’ = 0 có hai nghiệm phân biệt
⇔ (1) có hai nghiệm phân biệt
⇔ Giá trị tham số thuộc miền D nào đó (*)
Bước 2: Từ điều kiện cho trước dẫn tới một phương trình hoặc một bất phương trình theo tham số, giải phương trình này ta được tham số sau đó đối chiếu với điều kiện (*) và kết luận.
Xem thêm các bài viết liên quan hay, chi tiết:
Bài tập Cực trị của hàm số Toán 12 mới nhất
Trắc nghiệm Cực trị hàm số (có đáp án)
Trắc nghiệm Giá trị lớn nhất, giá trị nhỏ nhất của hàm số (có đáp án)
Câu 13:
23/07/2024Biết hàm số (C): có hai điểm cực trị là x1,x2. Đẳng thức nào sau đây đúng?
 Xem đáp án
Xem đáp án
Ta có:
Chọn D.
Câu 14:
21/07/2024Điểm cực tiểu của đồ thị hàm số (C): là
 Xem đáp án
Xem đáp án
Với
Với
Với x = 0 y = 0.
Hàm số đạt cực tiểu tại x = 0.
Chọn A.
Câu 15:
22/07/2024Một hàm số y=f(x) liên tục trên R và có đạo hàm . Hỏi hàm số đã cho có bao nhiêu điểm cực trị?
 Xem đáp án
Xem đáp án
Ta có:
Chỉ có
Chọn B.
Câu 16:
23/07/2024Cho hàm số y=f(x) có đạo hàm . Hỏi hàm số y=f(x) đạt cực đại tại điểm nào dưới đây?
 Xem đáp án
Xem đáp án
Ta có:
Chỉ có
Chọn D.
Câu 17:
11/10/2024Cho hàm số y = f(x) có đạo hàm f'(x) = x2019(x2020 - 1), . Hỏi hàm số có bao nhiêu điểm cực trị?
 Xem đáp án
Xem đáp án
Đáp án đúng: C.
*Phương pháp giải:
- Lấy đạo hàm hàm số
- để xét cực trị hàm số ta cho f'(x) = 0 rồi tim ra giá trị của x ( bội kép thì tính là 1 nghiệm )
*Lời giải
Ta có:
(đều là nghiệm bội lẻ)
Hàm số đạt cực trị tại x=0; x =
* Dạng bài toán về tìm cực trị hàm số:
Dạng 1. Tìm các điểm cực trị của hàm số.
cách 1:
- Tìm f’(x)
- Tìm các điểm xi (i = 1, 2, 3,…) tại đó đạo hàm bằng 0 hoặc hàm số liên tục nhưng không có đạo hàm
- Xét dấu của f’(x). Nếu f’(x) đổi dấu khi x qua điểm xo thì hàm số có cực trị tại điểm xo
cách 2:
- Tìm f’(x)
- Tìm các nghiệm xi (i = 1, 2, 3,…) của phương trình f ‘(x) = 0
- Với mỗi xi tính f ”(xi)
- Nếu f ”(xi) < 0 thì hàm số đạt cực đại tại điểm xi
- Nếu f ”(xi) > 0 thì hàm số đạt cực tiểu tại điểm xi
Dạng 2: Tìm điều kiện để hàm số có cực trị.
a, Cực trị của hàm số bậc ba:
Cho hàm số y = ax3 + bx2 + cx + d, a ≠ 0.
y’ = 0 ⇔ 3ax2 + 2bx + c = 0 (1) ; Δ’y’ = b2 – 3ac
- Phương trình (1) vô nghiệm hoặc có nghiệm kép thì hàm số đã cho không có cực trị.
→ Hàm số bậc 3 không có cực trị ⇔ b2 – 3ac ≤ 0
- Phương trình (1) có hai nghiệm phân biệt thì hàm số đã cho có 2 cực trị.
→ Hàm số bậc 3 có 2 cực trị ⇔ b2 – 3ac > 0
b, Cực trị của hàm số bậc bốn trùng phương:
Cho hàm số: y = ax4 + bx2 + c (a ≠ 0) có đồ thị là (C).
y' = 4ax3 + 2bx; y' = 0 ⇔ 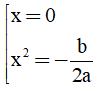
- Nếu (C)có một điểm cực trị thì y' = 0 có 1 nghiệm x = 0 ⇔ -b/2a ≤ 0 ⇔ ab ≥ 0.
- Nếu (C)có ba điểm cực trị thì y' = 0 có 3 nghiệm phân biệt ⇔ -b/2a > 0 ⇔ ab < 0.
Xem thêm các bài viết liên quan hay, chi tiết:
Câu 18:
11/07/2024Hàm số y=f(x) xác định, liên tục trên R và có bảng biến thiên
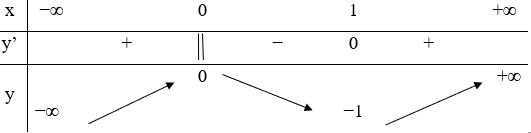
Khẳng định nào sau đây là khẳng định đúng?
 Xem đáp án
Xem đáp án
Hàm số đạt cực đại tại x=0 và đạt cực tiểu tại x=1
Chọn D.
Câu 19:
12/07/2024Hàm số y=f(x) có bảng biến thiên như hình vẽ bên. Mệnh đề nào dưới đây đúng
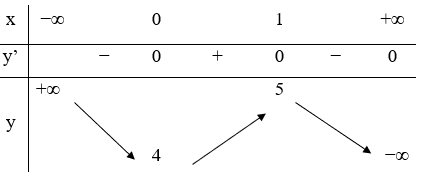
 Xem đáp án
Xem đáp án
Giá trị cực đại của hàm số là 5.
Chọn A.
Câu 20:
23/07/2024Cho hàm số y=f(x) có bảng biến thiên như sau
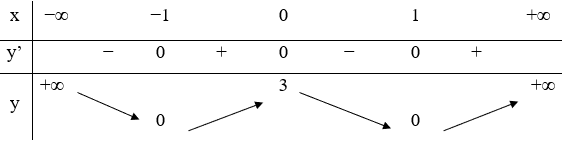
Mệnh đề nào dưới đây sai?
 Xem đáp án
Xem đáp án
Hàm số có giá trị cực đại bằng 3 nên đáp án C sai.
Chọn C.
Câu 21:
23/07/2024Hàm số y=f(x) xác định, liên tục trên đoạn [2;4] và có bảng biến thiên như sau
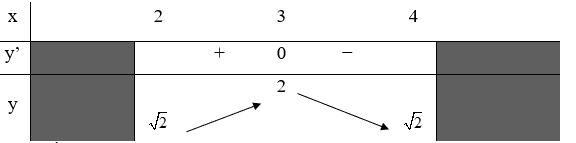
Mệnh đề nào sau đây đúng?
 Xem đáp án
Xem đáp án
Hàm số có một điểm cực trị.
Chọn B.
Câu 22:
21/07/2024Hàm số y=f(x) liên tục trên R và có bảng xét dấu đạo hàm như hình vẽ.

Hỏi hàm số có bao nhiêu điểm cực trị?
 Xem đáp án
Xem đáp án
Đạo hàm đổi dấu 3 lần nên hàm số có 3 điểm cực trị.
Chọn C.
Câu 23:
23/07/2024Hàm số y=f(x) xác định, liên tục trên R\{0} và có bảng xét dấu đạo hàm như hình vẽ.
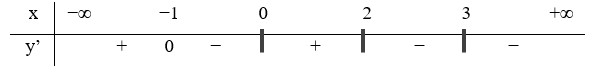
Hỏi hàm số có bao nhiêu điểm cực trị?
 Xem đáp án
Xem đáp án
Đạo hàm đổi dấu 3 lần nên hàm số có 3 điểm cực trị.
Chọn C.
Câu 24:
22/07/2024Hàm số y=f(x) xác định, liên tục trên R và có bảng xét dấu đạo hàm như hình vẽ.
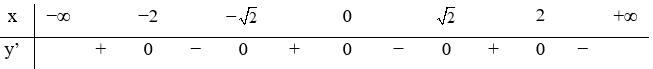
Hàm số y = f(-x) có bao nhiêu điểm cực trị?
 Xem đáp án
Xem đáp án
Ta có: (vì số lần đổi dấu của đạo hàm là như nhau)
Quan sát bảng xét dấu của hàm ta thấy đạo hàm đổi dấu 5 lần.
Vậy hàm số có 5 điểm cực trị.
Chọn D.
Câu 25:
23/07/2024Hàm số y = f(x) liên tục trên R và có bảng xét dấu đạo hàm như hình vẽ. Hỏi hàm số y = f(2x+1) có bao nhiêu điểm cực trị?
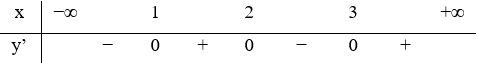
 Xem đáp án
Xem đáp án
Chọn
Ta có:
Vậy hàm số đã cho có 3 điểm cực trị.
Chọn A.
Câu 26:
15/07/2024Hàm số y =f(x) liên tục trên và có bảng biến thiên như hình vẽ.
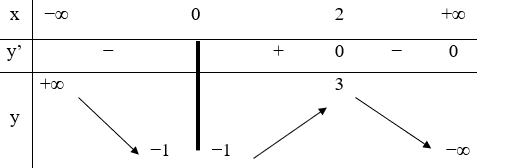
Khẳng định nào sau đây là khẳng định đúng?
 Xem đáp án
Xem đáp án
Hàm số đạt cực đại tại
Chọn C.
Câu 27:
23/07/2024Hàm số y=f(x) liên tục trên R và có bảng biến thiên như hình vẽ. Hàm số y=f(-x+1) đạt cực đại tại điểm
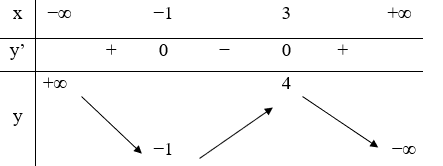
 Xem đáp án
Xem đáp án
Chọn
Ta có
Dựa vào bảng biến thiên, ta được là điểm cực đại của hàm số.
Chọn C.
Câu 28:
21/07/2024Hàm số y = f(x) liên tục trên R và có bảng biến thiên như hình vẽ bên.
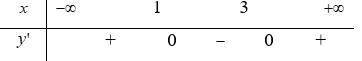
Hàm số g(x) = f(x-1) đạt cực tiểu tại điểm
 Xem đáp án
Xem đáp án
Chọn
Ta có:
Bảng xét dấu
Dựa vào bảng xét dấu, ta được là điểm cực tiểu của hàm số.
Chọn A.
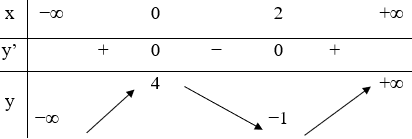
Câu 29:
23/07/2024Hàm số y=f(x) liên tục trên R và có bảng xét dấu đạo hàm như hình vẽ.
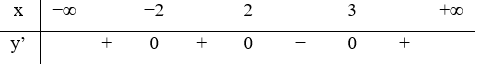
Số điểm cực trị của hàm số y=g(x)=f(1-x2) là
 Xem đáp án
Xem đáp án
Chọn
Do đó
Phương trình là nghiệm đơn
Vậy hàm số đã cho có duy nhất 1 điểm cực trị.
Chọn D.
Câu 30:
23/07/2024Hàm số y=f(x) liên tục trên và có bảng xét dấu đạo hàm như hình vẽ.
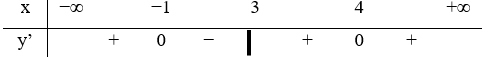
Số điểm cực trị của hàm số y = g(x) = f(x2+2x+3) là
 Xem đáp án
Xem đáp án
Hàm số
Chọn
Ta có
Bảng xét dấu
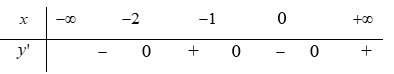
Dựa vào bảng xét dấu, ta được có 3 điểm cực trị.
Chọn C.
Có thể bạn quan tâm
- Trắc nghiệm Cực trị hàm số (có đáp án) (840 lượt thi)
- Bài tập Cực trị hàm số cơ bản, nâng cao có lời giải (P1) (321 lượt thi)
- 28 câu trắc nghiệm: Cực trị của hàm số có đáp án (323 lượt thi)
- Trắc nghiệm Cực trị của hàm số có đáp án (P1) (Nhận biết) (425 lượt thi)
- Trắc nghiệm Cực trị của hàm số có đáp án (P1) (Thông hiểu) (315 lượt thi)
- Trắc nghiệm Cực trị của hàm số có đáp án (P1) (Vận dụng) (328 lượt thi)
- Trắc nghiệm Cực trị của hàm số có đáp án (P1) (283 lượt thi)
Các bài thi hot trong chương
- Trắc nghiệm Sự đồng biến, nghịch biến của hàm số (có đáp án) (888 lượt thi)
- Bài tập về Tính đơn điệu của hàm số có lời giải (779 lượt thi)
- Trắc nghiệm Giá trị lớn nhất. Giá trị nhỏ nhất của hàm số (có đáp án) (645 lượt thi)
- Trắc nghiệm Khảo sát sự biến thiên và vẽ đồ thị hàm số (có đáp án) (488 lượt thi)
- Trắc nghiệm Khảo sát sự biến thiên và vẽ đồ thị của hàm số có đáp án (Phần 1) (467 lượt thi)
- Trắc nghiệm Đường tiệm cận (có đáp án) (443 lượt thi)
- Trắc nghiệm Khảo sát sự biến thiên và vẽ đồ thị của hàm số (có đáp án) (403 lượt thi)
- Trắc nghiệm Đường tiệm cận có đáp án (396 lượt thi)
- Trắc nghiệm Ôn tập Chương 1 - Ứng dụng đạo hàm để khảo sát và vẽ đồ thị của hàm số (có đáp án) (395 lượt thi)
- 250 câu trắc nghiệm Ứng dụng đạo hàm để khảo sát hàm số cơ bản (P1) (384 lượt thi)
