Câu hỏi:
09/10/2024 324Hàm số nào sau đây không có điểm cực trị
A. y =
B. y =
C. y =
D. y =
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng: B
*Phương pháp giải:
- Nắm vững lại kiến thức cũng như điều kiện để xác định cực trị của một hàm số
*Lời giải:
Hàm số y = x3 không có cực trị.
* Lý thuyết thêm về cực trị hàm số:
+) Điều kiện cần để hàm số có cực trị.
Định lý 1: Giả sử hàm số f(x) đạt cực trị tại điểm xo. Khi đó, nếu f(x) có đạo hàm tại điểm xo thì f‘(xo) = 0.
+) Điều kiện đủ để hàm số có cực trị.
Định lý 2: Giả sử hàm số y = f(x) liên tục trên K = ( x0 -h: x0 +h ) và có đạo hàm trên K hoặc trên , với h >0 .
- Nếu f '(x) > 0 trên khoảng (x0 - h; x0) và trên thì x0 là một điểm cực đại của hàm số f(x) .
- Nếu f '(x) < 0 trên khoảng (x0 - h; x0) và f '(x) > 0 trên thì x0 là một điểm cực tiểu của hàm số f(x) .
Định lý 3: Giả sử hàm số f có đạo hàm cấp một trên khoảng (a; b) chứa điểm xo ; f ‘(xo) = 0 và f có đạo hàm cấp hai khác 0 tại điểm xo
a) Nếu f ”(xo) < 0 thì hàm số f đạt cực đại tại điểm xo
b) Nếu f ”(xo) < 0 thì hàm số f đạt cực tiểu tại điểm xo
* Dạng bài về cực trị hàm số:
a) Dạng 1. Tìm các điểm cực trị của hàm số.
* Phương pháp giải.
Quy tắc 1: Áp dụng định lý 2
- Tìm f’(x)
- Tìm các điểm xi (i = 1, 2, 3,…) tại đó đạo hàm bằng 0 hoặc hàm số liên tục nhưng không có đạo hàm
- Xét dấu của f’(x). Nếu f’(x) đổi dấu khi x qua điểm xo thì hàm số có cực trị tại điểm xo
Quy tắc 2: Áp dụng định lý 3
- Tìm f’(x)
- Tìm các nghiệm xi (i = 1, 2, 3,…) của phương trình f ‘(x) = 0
- Với mỗi xi tính f ”(xi)
- Nếu f ”(xi) < 0 thì hàm số đạt cực đại tại điểm xi
- Nếu f ”(xi) > 0 thì hàm số đạt cực tiểu tại điểm xi
b) Dạng 2: Tìm điều kiện để hàm số có cực trị.
* Phương pháp. Sử dụng định lí 2 và định lí 3
* Cực trị của hàm số bậc ba: Cho hàm số y = ax3 + bx2 + cx + d, a ≠ 0.
y’ = 0 ⇔ 3ax2 + 2bx + c = 0 (1) ; Δ’y’ = b2 – 3ac
- Phương trình (1) vô nghiệm hoặc có nghiệm kép thì hàm số đã cho không có cực trị.
→ Hàm số bậc 3 không có cực trị ⇔ b2 – 3ac ≤ 0
- Phương trình (1) có hai nghiệm phân biệt thì hàm số đã cho có 2 cực trị.
→ Hàm số bậc 3 có 2 cực trị ⇔ b2 – 3ac > 0
c) Dạng 3: Tìm điều kiện để các điểm cực trị của hàm số thỏa mãn điều kiện cho trước.
* Phương pháp giải: Hàm số bậc ba y = ax3 + bx2 + cx + d (a ≠ 0, a, b, c, d phụ thuộc vào tham số)
Bước 1: Tính y’ = 3ax2 + 2bx + c, y’ = 0 ⇔ 3ax2 +2bx + c = 0 (1)
Để hàm số có cực đại, cực tiểu ⇔ y’ = 0 có hai nghiệm phân biệt
⇔ (1) có hai nghiệm phân biệt
⇔ Giá trị tham số thuộc miền D nào đó (*)
Bước 2: Từ điều kiện cho trước dẫn tới một phương trình hoặc một bất phương trình theo tham số, giải phương trình này ta được tham số sau đó đối chiếu với điều kiện (*) và kết luận.
Xem thêm các bài viết liên quan hay, chi tiết:
Bài tập Cực trị của hàm số Toán 12 mới nhất
Trắc nghiệm Cực trị hàm số (có đáp án)
Trắc nghiệm Giá trị lớn nhất, giá trị nhỏ nhất của hàm số (có đáp án)
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 2:
Hàm số y = f(x) liên tục trên R và có bảng xét dấu đạo hàm như hình vẽ. Hỏi hàm số y = f(2x+1) có bao nhiêu điểm cực trị?
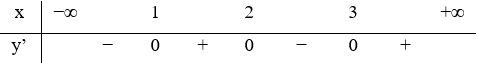
Câu 3:
Hàm số y=f(x) xác định, liên tục trên R\{0} và có bảng xét dấu đạo hàm như hình vẽ.
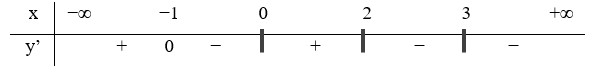
Hỏi hàm số có bao nhiêu điểm cực trị?
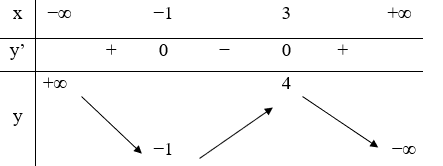
Câu 5:
Hàm số y=f(x) liên tục trên R và có bảng biến thiên như hình vẽ. Hàm số y=f(-x+1) đạt cực đại tại điểm
Câu 6:
Đồ thị của hàm số y = -x3 + 3x +5 có hai điểm cực trị A và B. Tính diện tích S của tam giác OAB với O là gốc tọa độ.
Câu 7:
Cho hàm số y=f(x) có bảng biến thiên như sau
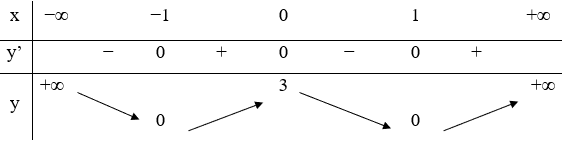
Mệnh đề nào dưới đây sai?
Câu 8:
Biết hàm số (C): có hai điểm cực trị là x1,x2. Đẳng thức nào sau đây đúng?
Câu 9:
Hàm số y=f(x) xác định, liên tục trên đoạn [2;4] và có bảng biến thiên như sau
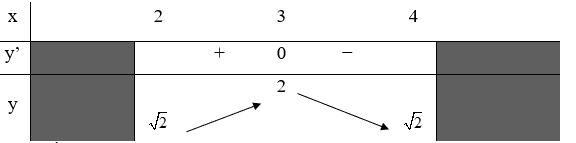
Mệnh đề nào sau đây đúng?
Câu 10:
Cho hàm số y = f(x) có đạo hàm f'(x) = x2019(x2020 - 1), . Hỏi hàm số có bao nhiêu điểm cực trị?
Câu 12:
Hàm số y=f(x) liên tục trên và có bảng xét dấu đạo hàm như hình vẽ.
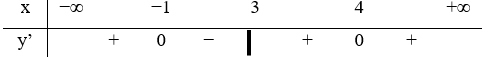
Số điểm cực trị của hàm số y = g(x) = f(x2+2x+3) là
Câu 13:
Hàm số y =f(x) liên tục trên và có bảng biến thiên như hình vẽ.
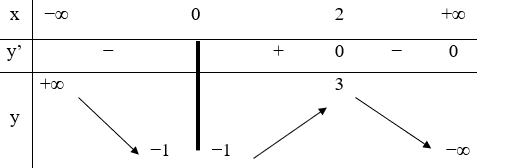
Khẳng định nào sau đây là khẳng định đúng?
Câu 14:
Hàm số y=f(x) liên tục trên R và có bảng xét dấu đạo hàm như hình vẽ.
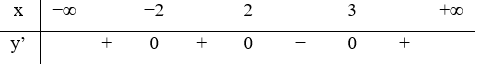
Số điểm cực trị của hàm số y=g(x)=f(1-x2) là


