Câu hỏi:
11/10/2024 1,660Cho hàm số y = f(x) có đạo hàm f'(x) = x2019(x2020 - 1), ∀x∈R . Hỏi hàm số có bao nhiêu điểm cực trị?
A. 1
B. 2
C. 3
D. Vô số
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng: C.
*Phương pháp giải:
- Lấy đạo hàm hàm số
- để xét cực trị hàm số ta cho f'(x) = 0 rồi tim ra giá trị của x ( bội kép thì tính là 1 nghiệm )
*Lời giải
Ta có: f'
(đều là nghiệm bội lẻ)
Hàm số đạt cực trị tại x=0; x =
* Dạng bài toán về tìm cực trị hàm số:
Dạng 1. Tìm các điểm cực trị của hàm số.
cách 1:
- Tìm f’(x)
- Tìm các điểm xi (i = 1, 2, 3,…) tại đó đạo hàm bằng 0 hoặc hàm số liên tục nhưng không có đạo hàm
- Xét dấu của f’(x). Nếu f’(x) đổi dấu khi x qua điểm xo thì hàm số có cực trị tại điểm xo
cách 2:
- Tìm f’(x)
- Tìm các nghiệm xi (i = 1, 2, 3,…) của phương trình f ‘(x) = 0
- Với mỗi xi tính f ”(xi)
- Nếu f ”(xi) < 0 thì hàm số đạt cực đại tại điểm xi
- Nếu f ”(xi) > 0 thì hàm số đạt cực tiểu tại điểm xi
Dạng 2: Tìm điều kiện để hàm số có cực trị.
a, Cực trị của hàm số bậc ba:
Cho hàm số y = ax3 + bx2 + cx + d, a ≠ 0.
y’ = 0 ⇔ 3ax2 + 2bx + c = 0 (1) ; Δ’y’ = b2 – 3ac
- Phương trình (1) vô nghiệm hoặc có nghiệm kép thì hàm số đã cho không có cực trị.
→ Hàm số bậc 3 không có cực trị ⇔ b2 – 3ac ≤ 0
- Phương trình (1) có hai nghiệm phân biệt thì hàm số đã cho có 2 cực trị.
→ Hàm số bậc 3 có 2 cực trị ⇔ b2 – 3ac > 0
b, Cực trị của hàm số bậc bốn trùng phương:
Cho hàm số: y = ax4 + bx2 + c (a ≠ 0) có đồ thị là (C).
y' = 4ax3 + 2bx; y' = 0 ⇔ 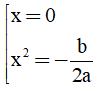
- Nếu (C)có một điểm cực trị thì y' = 0 có 1 nghiệm x = 0 ⇔ -b/2a ≤ 0 ⇔ ab ≥ 0.
- Nếu (C)có ba điểm cực trị thì y' = 0 có 3 nghiệm phân biệt ⇔ -b/2a > 0 ⇔ ab < 0.
Xem thêm các bài viết liên quan hay, chi tiết:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 2:
Hàm số y = f(x) liên tục trên R và có bảng xét dấu đạo hàm như hình vẽ. Hỏi hàm số y = f(2x+1) có bao nhiêu điểm cực trị?
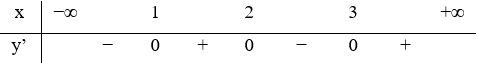
Câu 3:
Hàm số y=f(x) xác định, liên tục trên R\{0} và có bảng xét dấu đạo hàm như hình vẽ.
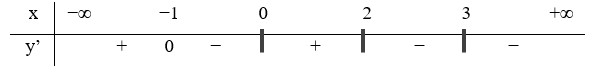
Hỏi hàm số có bao nhiêu điểm cực trị?
Câu 5:
Hàm số y=f(x) liên tục trên R và có bảng biến thiên như hình vẽ. Hàm số y=f(-x+1) đạt cực đại tại điểm
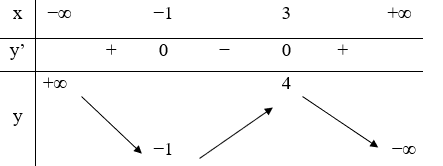
Câu 6:
Đồ thị của hàm số y = -x3 + 3x +5 có hai điểm cực trị A và B. Tính diện tích S của tam giác OAB với O là gốc tọa độ.
Câu 7:
Cho hàm số y=f(x) có bảng biến thiên như sau
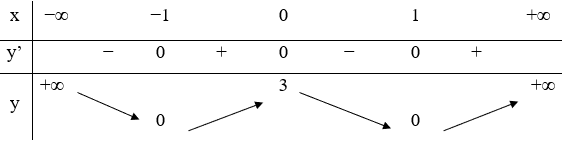
Mệnh đề nào dưới đây sai?
Câu 8:
Biết hàm số (C): có hai điểm cực trị là x1,x2. Đẳng thức nào sau đây đúng?
Câu 9:
Hàm số y=f(x) xác định, liên tục trên đoạn [2;4] và có bảng biến thiên như sau
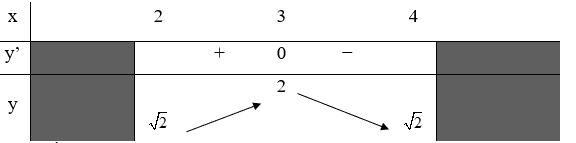
Mệnh đề nào sau đây đúng?
Câu 11:
Hàm số y=f(x) liên tục trên và có bảng xét dấu đạo hàm như hình vẽ.
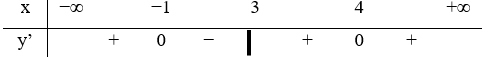
Số điểm cực trị của hàm số y = g(x) = f(x2+2x+3) là
Câu 12:
Hàm số y =f(x) liên tục trên và có bảng biến thiên như hình vẽ.
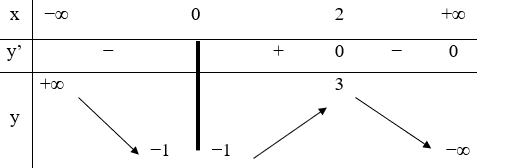
Khẳng định nào sau đây là khẳng định đúng?
Câu 13:
Hàm số y=f(x) liên tục trên R và có bảng xét dấu đạo hàm như hình vẽ.
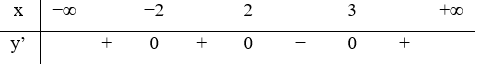
Số điểm cực trị của hàm số y=g(x)=f(1-x2) là
Câu 15:
Hàm số y=f(x) xác định, liên tục trên R và có bảng xét dấu đạo hàm như hình vẽ.
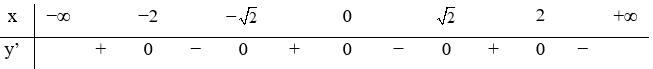
Hàm số y = f(-x) có bao nhiêu điểm cực trị?


