Trắc nghiệm Sự đồng biến, nghịch biến của hàm số (có đáp án)
Trắc nghiệm Toán 12 Bài 1: Sự đồng biến, nghịch biến của hàm số
-
958 lượt thi
-
28 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
18/07/2024Cho hàm số y=x+11−x. Khẳng định nào sao đây là khẳng định đúng?
 Xem đáp án
Xem đáp án
TXĐ: D=ℝ\ .
Ta có
Hàm số đồng biến trên các khoảng
.
Chọn D.
Câu 2:
17/07/2024Cho hàm số . Khẳng định nào sau đây là khẳng định đúng?
 Xem đáp án
Xem đáp án
TXĐ: .
Ta có .
Chọn B.
Câu 3:
21/07/2024Cho hàm số . Khẳng định nào sau đây là khẳng định đúng?
 Xem đáp án
Xem đáp án
TXĐ: .
Ta có
Do đó hàm số đã cho luôn nghịch biến trên .
Chọn A.
Câu 6:
18/07/2024Hàm số đồng biến trên các khoảng (các khoảng) nào sau đây?
 Xem đáp án
Xem đáp án
Ta có:
.
Chọn C.
Câu 7:
21/07/2024Trên các khoảng nghịch biến của hàm số có chứa bao nhiêu số nguyên âm?
 Xem đáp án
Xem đáp án
.
Chọn D.
Câu 8:
20/07/2024Cho hàm số . Khẳng định nào sau đây là khẳng định đúng?
 Xem đáp án
Xem đáp án
Ta có: .
Chọn C.
Câu 10:
11/12/2024Cho hàm số có bảng biến thiên như sau:
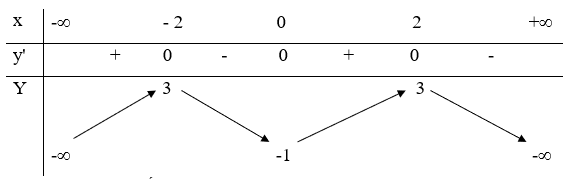
Hàm số nghịch biến trên khoảng nào dưới đây?
 Xem đáp án
Xem đáp án
Đáp án đúng là A
Lời giải
Dựa vào bảng biến thiên, ta có:
Hàm số nghịch biến trên
*Phương pháp giải:
Quan sát đồ thị và kết luận
*Lý thuyết:
1. Nhắc lại định nghĩa
- Định nghĩa:
Kí hiệu K là khoảng hoặc đoạn hoặc nửa khoảng. Giả sử hàm số y = f(x) xác định trên K. Ta nói:
Hàm số y = f(x) đồng biến (tăng) trên K nếu với mọi cặp x1; x2 thuộc K mà x1 nhỏ hơn x2 thì f(x1) nhỏ hơn f(x2), tức là
x1 < x2 f(x1) < f(x2).
Hàm số y = f(x) nghịch biến (giảm) trên K nếu với mọi cặp x1; x2 thuộc K mà x1 nhỏ hơn x2 thì f(x1) lớn hơn f(x2), tức là
x1 < x2 f(x1) > f(x2).
- Hàm số đồng biến hoặc nghịch biến trên K được gọi chung là hàm số đơn điệu trên K.
- Nhận xét: Từ định nghĩa trên ta thấy:
a) f(x) đồng biến trên K
f(x) nghịch biến trên K
b) Nếu hàm số đồng biến trên K thì đồ thị đi lên từ trái sang phải.
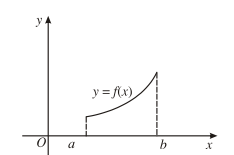
Nếu hàm số nghịch biến trên K thì đồ thị đi xuống từ trái sang phải.
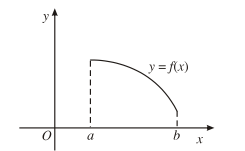
2. Tính đơn điệu và dấu của đạo hàm
- Định lí:
Cho hàm số y = f(x) có đạo hàm trên K.
a) Nếu f’(x) > 0 với mọi x thuộc K thì hàm số f(x) đồng biến trên K.
b) Nếu f’(x) < 0 với mọi x thuộc K thì hàm số f(x) nghịch biến trên K.
- Chú ý:
Nếu f’(x) = 0 với thì f(x) không đổi trên K.
- Chú ý:
Ta có định lí mở rộng sau đây:
Giả sử hàm số y = f(x) có đạo hàm trên K. Nếu
Và f’(x) = 0 chỉ tại một số hữu hạn điểm thì hàm số đồng biến (nghịch biến) trên K.
Xem thêm
Lý thuyết Sự đồng biến, nghịch biến của hàm số (mới 2 + Bài Tập) – Toán 12
Câu 11:
22/07/2024Cho hàm số . Hàm số đã cho nghịch biến trên khoảng nào sau đây?
 Xem đáp án
Xem đáp án
TXĐ: .
.
Ta có bảng biến thiên:
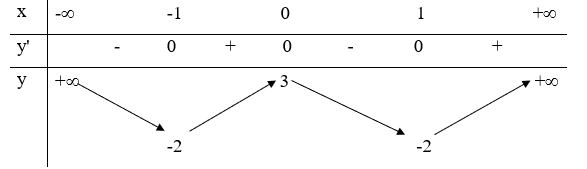
Vậy hàm số nghịch biến trên
Chọn A.
Câu 12:
22/07/2024Cho hàm số có bảng biến thiên như sau:
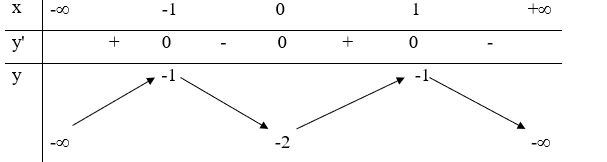
Hàm số đã cho đồng biến trên khoảng nào sau đây?
 Xem đáp án
Xem đáp án
Dựa vào bảng biến thiên, ta có:
Hàm số .
Chọn D.
Câu 13:
21/07/2024Hàm số và có bảng biến thiên như sau:
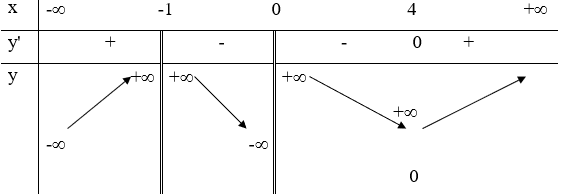
Hỏi hàm số đồng biến trên khoảng (các khoảng) nào dưới đây?
 Xem đáp án
Xem đáp án
Dựa vào bảng biến thiên, ta có:
Hàm số .
Chọn B.
Câu 14:
23/07/2024Hàm số và có bảng biến thiên như sau:
Khẳng định nào sau đây là khẳng định đúng?
 Xem đáp án
Xem đáp án
Dựa vào bảng biến thiên, ta có:
Hàm số đồng biến trên khoảng .
Chọn C.
(Ngoài ra còn có cách kết luận khác là hàm số đồng biến trên từng khoảng xác định của nó).
Câu 15:
20/07/2024Hàm số có bảng biến thiên như hình vẽ sau:
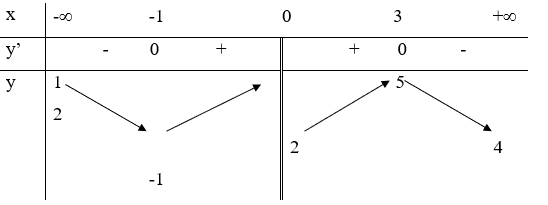
Khẳng định nào sau đây là khẳng định đúng?
 Xem đáp án
Xem đáp án
Dựa vào bảng biến thiên, ta có:
Hàm số nghịch biến trên các khoảng (-) .
Chọn D.
Câu 16:
13/07/2024Hàm số có bảng biến thiên như sau:
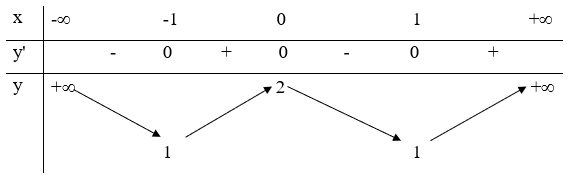
Khẳng định nào sau đây là khẳng định sai?
 Xem đáp án
Xem đáp án
Dựa vào bảng biến thiên, ta thấy:
Hàm số nghịch biến trên (0; 1) nên f(1) < f(0).
Do đó đáp án C sai.
Chọn C.
Câu 17:
20/07/2024Hàm số có bảng biến thiên như sau:
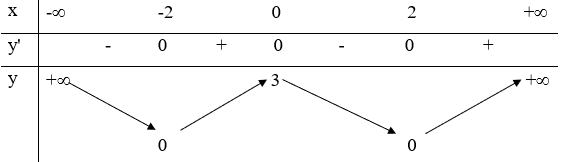
Khẳng định nào sau đây là khẳng định sai?
 Xem đáp án
Xem đáp án
Dựa vào bảng biến thiên, ta thấy:
Hàm số nghịch biến trên (-; -2) và (0; 2).
Do đó A đúng.
Hàm số đồng biến trên (-2; 0) và (2; +).
Do đó B đúng.
Ta thấy các giá trị của
Do đó C đúng.
Hàm số không đồng biến trên (0; 3) và (0; +).
Do đó D sai.
Chọn D.
Câu 18:
20/07/2024Hàm số có bảng biến thiên như sau:
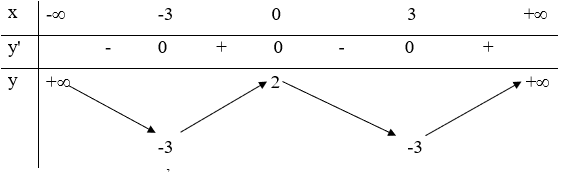
Khẳng định nào sau đây là khẳng định sai?
 Xem đáp án
Xem đáp án
Dựa vào bảng biến thiên, ta thấy rằng:
Hàm số nghịch biến trên các khoảng .
Do đó A đúng.
Tập giá trị của hàm số .
Do đó B đúng.
Hàm số nghịch biến trên khoảng .
Do đó D đúng.
Chọn C.
Câu 19:
22/07/2024Hàm số có bảng biến thiên như sau:
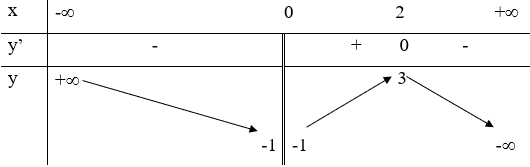
Khẳng định nào sau đây là khẳng định đúng?
 Xem đáp án
Xem đáp án
Dựa vào bảng biến thiên, ta thấy rằng
Hàm số nghịch biến trên khoảng .
Do đó A đúng.
Tập giá trị của hàm số .
Do đó B sai.
Hàm số bị gián đoạn trên .
Do đó C sai.
Hàm số đồng biến trên khoảng .
Do đó D sai.
Chọn A.
Câu 20:
22/07/2024Tìm tất cả các giá trị thực của tham số m sao cho hàm số giảm trên các khoảng mà nó xác định ?
 Xem đáp án
Xem đáp án
Tập xác định:
Để hàm số giảm trên các khoảng mà nó xác định .
Chọn D.
Câu 21:
13/07/2024Tìm tất cả các giá trị thực của tham số m sao cho hàm số ?
 Xem đáp án
Xem đáp án
Tập xác định: .
Để hàm số nghịch biến trên .
Chọn A.
Câu 22:
17/07/2024Tìm tất cả các giá trị thực của tham số m sao cho hàm số ?
 Xem đáp án
Xem đáp án
Tập xác định:
Hàm số đồng biến trên
Trường hợp 1: m = 0 ta có
Trường hợp 2: m > 0 ta có
Trường hợp 3: m < 0 ta có
Vậy .
Chọn A.
Câu 23:
21/07/2024Tìm tất cả các giá trị thực của tham số m sao cho hàm số luôn nghịch biến trên ?
 Xem đáp án
Xem đáp án
Tập xác định:
Hàm số nghịch biến trên
Trường hợp 1: .
Trường hợp 2:
Trường hợp 3: ta có:
.
Vậy .
Chọn A.
Câu 24:
23/07/2024Tìm giá trị nhỏ nhất của tham số m sao cho hàm số ?
 Xem đáp án
Xem đáp án
Tập xác định:
Hàm số đồng biến trên
Vậy giá trị nhỏ nhất của m để hàm số đồng biến trên .
Chọn C.
Câu 25:
23/07/2024Tìm số nguyên m nhỏ nhất sao cho hàm số luôn nghịch biến trên các khoảng xác định của nó?
 Xem đáp án
Xem đáp án
Tập xác định: .
Ta có
Yêu cầu đề bài
Vậy không có số nguyên m nào thuộc khoảng .
Chọn D.
Câu 26:
13/07/2024Tìm tất cả các giá trị thực của tham số m sao cho hàm số ?
 Xem đáp án
Xem đáp án
Tập xác định .
Để hàm số giảm trên khoảng
.
Chọn C.
Câu 27:
20/07/2024Tìm tất cả các giá trị thực của tham số m sao cho hàm số ?
 Xem đáp án
Xem đáp án
Cách 1:Tập xác định: .
Ta có
Trường hợp 1:
Hàm số đồng biến trên R
Trường hợp 2: Hàm số đồng biến trên (*)
Trường hợp 2.1: là x = 4 (không thỏa (*))
Trường hợp 2.2:
Cách 2: Hàm số đồng biến trên
.
Lập bảng biến thiên của g(x) trên .
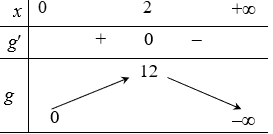
Chọn D.
Câu 28:
22/07/2024Tìm tất cả các giá trị thực của tham số m sao cho hàm số ?
 Xem đáp án
Xem đáp án
Tập xác định .
Hàm số đồng biến trên
Lập bảng biến thiên của g(x) trên .
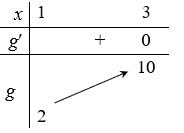
Dựa vào bảng biến thiên, kết luận: .
Chọn B.
Có thể bạn quan tâm
- Trắc nghiệm Sự đồng biến, nghịch biến của hàm số (có đáp án) (957 lượt thi)
- Bài tập về Tính đơn điệu của hàm số có lời giải (875 lượt thi)
- 21 câu trắc nghiệm: Sự đồng biến nghịch biến của hàm số có đáp án (388 lượt thi)
- Trắc nghiệm Sự đồng biến, nghịch biến của hàm số có đáp án (Nhận biết) (323 lượt thi)
- Trắc nghiệm Sự đồng biến, nghịch biến của hàm số có đáp án (P1) (Thông hiểu) (367 lượt thi)
- Trắc nghiệm Sự đồng biến, nghịch biến của hàm số có đáp án (P1) (Vận dụng) (425 lượt thi)
- Trắc nghiệm Sự đồng biến, nghịch biến của hàm số có đáp án (410 lượt thi)
Các bài thi hot trong chương
- Trắc nghiệm Cực trị hàm số (có đáp án) (893 lượt thi)
- Trắc nghiệm Giá trị lớn nhất. Giá trị nhỏ nhất của hàm số (có đáp án) (713 lượt thi)
- Trắc nghiệm Khảo sát sự biến thiên và vẽ đồ thị hàm số (có đáp án) (552 lượt thi)
- Trắc nghiệm Khảo sát sự biến thiên và vẽ đồ thị của hàm số có đáp án (Phần 1) (527 lượt thi)
- Trắc nghiệm Đường tiệm cận (có đáp án) (502 lượt thi)
- Trắc nghiệm Cực trị của hàm số có đáp án (P1) (Nhận biết) (482 lượt thi)
- Trắc nghiệm Khảo sát sự biến thiên và vẽ đồ thị của hàm số (có đáp án) (471 lượt thi)
- 250 câu trắc nghiệm Ứng dụng đạo hàm để khảo sát hàm số cơ bản (P1) (455 lượt thi)
- Trắc nghiệm Ôn tập Chương 1 - Ứng dụng đạo hàm để khảo sát và vẽ đồ thị của hàm số (có đáp án) (448 lượt thi)
- Trắc nghiệm Đường tiệm cận có đáp án (447 lượt thi)
