28 câu hỏi trắc nghiệm thuộc Trắc nghiệm Toán 12 Bài Ôn tập Chương 1 - Ứng dụng đạo hàm để khảo sát và vẽ đồ thị của hàm số

Câu 1:

21/07/2024

Biết rằng đồ thị hàm số $y = x^{2} - 3 x + 1$ tại hai điểm phân biệt A và B. Tính độ dài đoạn thẳng AB.

A. AB=3

B. AB=2 $\sqrt{2}$

C. AB=2

D. AB=1

Xem đáp án

Xét phương trình hoành độ giao điểm:

$x^{3} - 3 x^{2} + 2 x - 1 = x^{2} - 3 x + 1$

$\Leftrightarrow x^{3} - 4 x^{2} + 5 x - 2 = 0$

$\Leftrightarrow x^{3} - 2 x^{2} + x - 2 x^{2} + 4 x - 2 = 0$

$\Leftrightarrow (x - 2) {(x - 1)}^{2} = 0$

$\Leftrightarrow [\begin{array}{l} x = 1 \\ x = 2 \end{array}$

$\Rightarrow [\begin{array}{l} y = - 1 \\ y = - 1 \end{array}$

$\Rightarrow A (1; - 1), B (2; - 1)$

$\Rightarrow \vec{A B} (1; 0) \Rightarrow A B = \sqrt{1^{2}} = 1.$

Chọn D.

Câu 2:

18/07/2024

Tìm tất cả các giá trị của tham số m để đồ thị hàm số $y = (x - 1) (x^{2} + m x + m)$ cắt trục hoành tại ba điểm phân biệt.

Xem đáp án

Trục hoành: y = 0.

Xét phương trình hoành độ giao điểm:

$(x - 1) (x^{2} + m x + m) = 0$

$\Leftrightarrow [\begin{array}{l} x = 1 \\ x^{2} + m x + m = 0 (1) \end{array}$

Để đồ thị hàm số $y = (x - 1) (x^{2} + m x + m)$ cắt trục hoành tại ba điểm phân biệt thì phương trình (1) phải có hai nghiệm phân biệt khác 1.

Nghĩa là:

$\{\begin{cases} 1^{2} + m .1 + m \neq 0 \\ Δ = m^{2} - 4 m > 0 \end{cases}$

$\Leftrightarrow {\begin{cases} m \neq - \frac{1}{2} \\ [\begin{array}{l} m < 0 \\ m > 4 \end{array} \end{cases}$ .

Vậy ;0)∪(4;+∞).

$m \in (- \infty; - \frac{1}{2}) \cup (- \frac{1}{2}; 0) \cup (4; + \infty) .$

Câu 3:

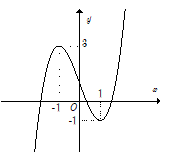
12/07/2024

Cho hàm số $f (x) + m - 2018 = 0$ có duy nhất một nghiệm.

A. m=2015, m=2019

B. 2015<m<2019

C. m<2015, m>2019

D. m≤2015, m≥2019

Xem đáp án

Xét phương trình $f (x) = - m + 2018$

Để đường thẳng y = - m + 2018 cắt f(x) tại 1 điểm thì

$[\begin{array}{l} - m + 2018 < - 1 \\ - m + 2018 > 3 \end{array}$

$\Leftrightarrow [\begin{array}{l} m > 2019 \\ m < 2015 \end{array}$ .

Chọn C.

Câu 4:

19/07/2024

Cho hàm số $y = \frac{3 x - 1}{- 4 + 2 x}$ . Khẳng định nào sau đây là khẳng định đúng?

A. Hàm số luôn nghịch biến trên R

B. Hàm số luôn nghịch biến trên từng khoảng xác định.

C. Hàm số đồng biến trên các khoảng (−∞;2) và (2;+∞)

D. Hàm số nghịch biến trên các khoảng (−∞;−2) và (−2;+∞)

Xem đáp án

TXĐ: $D = ℝ \ \{2\}$ .

Ta có $y' = - \frac{10}{{(- 4 + 2 x)}^{2}} < 0, \forall x \in D$ .

Chọn B.

Câu 5:

23/07/2024

Trên các khoảng nghịch biến của hàm số $y = \frac{x^{2} - 3 x - 1}{2 + x}$ có chứa bao nhiêu số nguyên âm?

A. 1.

B. 4.

C. 2.

D. 3.

Xem đáp án

$y^{'} = \frac{(2 x - 3) (2 + x) - (x^{2} - 3 x - 1)}{{(2 + x)}^{2}}$

$= \frac{x^{2} + 4 x - 5}{{(2 + x)}^{2}} < 0$

$\Leftrightarrow {\begin{cases} x \neq - 2 \\ x^{2} + 4 x - 5 < 0 \end{cases}$

$\Leftrightarrow \{\begin{cases} x \neq - 2 \\ - 5 < x < 1 \end{cases}$

$\Rightarrow x \in {- 4; - 3; - 1}$ .

Chọn D.

Câu 6:

23/07/2024

Cho hàm số $y = f (x)$ có bảng biến thiên như sau:

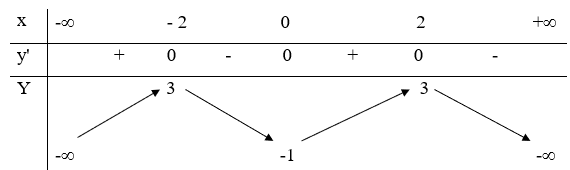
Hàm số $y = f (x)$ nghịch biến trên khoảng nào dưới đây?

A. (-2; 0)

B. (-∞; -2)

C. (0; 2)

D. (0; +∞)

Xem đáp án

Dựa vào bảng biến thiên, ta có:

Hàm số nghịch biến trên $(- 2; 0) \cup (2; + \infty) .$

Chọn A.

Câu 7:

21/07/2024

Hàm số xác định trên và có bảng biến thiên như sau:

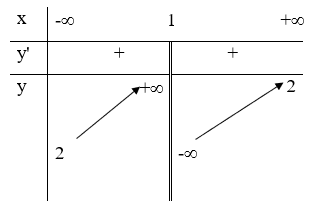
Khẳng định nào sau đây là khẳng định đúng?

A. Hàm số đồng biến trên khoảng (-∞; 1) ∪∪ (1; +∞)

B. Hàm số đồng biến trên khoảng (-∞; 2) ∪∪ (2; +∞)

C. Hàm số đồng biến trên khoảng (-∞; -1) và (1; +∞)

D. Hàm số đồng biến trên R\{1}

Xem đáp án

Dựa vào bảng biến thiên, ta có:

Hàm số đồng biến trên khoảng $(1; + \infty)$ .

Chọn C.

(Ngoài ra còn có cách kết luận khác là hàm số đồng biến trên từng khoảng xác định của nó).

Câu 8:

16/07/2024

Tìm tất cả các giá trị thực của tham số m sao cho hàm số

$ℝ$ ?

A. −3≤m≤1

B. m≤1

C. −3<m<1

D. m≤−3;m≥1

Xem đáp án

Tập xác định: $D = ℝ$ .

Ta có $y^{'} = - x^{2} - 2 m x + 2 m - 3$ .

Để hàm số nghịch biến trên $ℝ$ thì

$y^{'} \leq 0, \forall x \in ℝ$

$\Leftrightarrow {\begin{cases} a_{y^{'}} < 0 \\ Δ^{'} \leq 0 \end{cases}$

$\Leftrightarrow \{\begin{cases} - 1 < 0 (h n) \\ m^{2} + 2 m - 3 \leq 0 \end{cases}$

$\Leftrightarrow - 3 \leq m \leq 1$

Chọn A.

Câu 9:

21/07/2024

Tìm tất cả các giá trị thực của tham số m sao cho hàm số $ℝ$ ?

A. |m|≤1

B. m> $\frac{\sqrt{3}}{2}$

C. |m|≥1

D. m< $\frac{1}{2}$

Xem đáp án

Tập xác định: $D = ℝ$ .

Ta có $y^{'} = 1 - m \sin x$ .

Hàm số đồng biến trên $ℝ$

$\Leftrightarrow y' \geq 0, \forall x \in ℝ$

$\Leftrightarrow m \sin x \leq 1, \forall x \in ℝ$

Trường hợp 1: m = 0 ta có $0 \leq 1, \forall x \in ℝ$ .

Vậy hàm số luôn đồng biến trên $ℝ$

Trường hợp 2: m > 0 ta có

$\sin x \leq \frac{1}{m}, \forall x \in ℝ$

$\Leftrightarrow \frac{1}{m} \geq 1 \Leftrightarrow m \leq 1$

Trường hợp 3: m < 0 ta có

$\sin x \geq \frac{1}{m}, \forall x \in ℝ$

$\Leftrightarrow \frac{1}{m} \leq - 1 \Leftrightarrow m \geq - 1$

Vậy $|m| \leq 1$ .

Chọn A.

Câu 10:

23/07/2024

Đồ thị của hàm số y = -x³ + 3x² +5x có hai điểm cực trị A và B. Tính diện tích S của tam giác OAB với O là gốc tọa độ.

A. S = 9

B. S = $\frac{10}{3}$

C. S = 5

D. S = 10

Xem đáp án

Ta có: $y' = - 3 x^{2} + 6 x; y' = 0$

$\Leftrightarrow [\begin{array}{l} x = 0 \Rightarrow y = 5 \\ x = 2 \Rightarrow y = 9 \end{array}$

$\Rightarrow A (0; 5), B (2; 9)$

Ta có:

$S_{O A B} = \frac{1}{2} d (B, O y) . O A$

$= \frac{1}{2} . 2.5 = 5$

Chọn C.

Câu 11:

23/07/2024

Cực đại (giá trị cực đại) của hàm số y = -x⁴ + 2x² - 2 bằng

A. 1

B. -1

C. -2

D. 0

Xem đáp án

Ta có:

$y' = - 4 x^{3} + 4 x; y' = 0$

$\Leftrightarrow [\begin{array}{l} x = 0 \Rightarrow y_{C T} = - 2 \\ x = \pm 1 \Rightarrow y_{C Đ} = - 1 \end{array}$

Chọn B.

Câu 12:

21/07/2024

Hàm số y = f(x) xác định, liên tục trên R và có bảng biến thiên

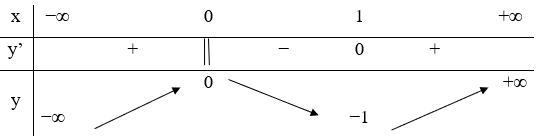
Khẳng định nào sau đây là khẳng định đúng?

A. Hàm số có đúng một cực trị

B. Hàm số có giá trị cực tiểu bằng 1

C. Hàm số có giá trị lớn nhất bằng 0 và giá trị nhỏ nhất bằng -1

D. Hàm số đạt cực đại tại x = 0 và đạt cực tiểu tại x = 1

Xem đáp án

Hàm số đạt cực đại tại x = 0 và đạt cực tiểu tại x = 1

Chọn D.

Câu 13:

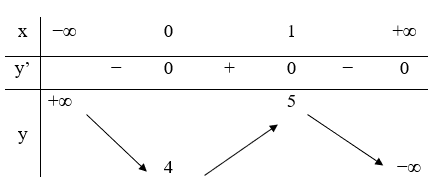
23/07/2024

Hàm số y = f(x) có bảng biến thiên như hình vẽ bên. Mệnh đề nào dưới đây đúng

A. $y_{C Đ}$ =5

B. $y_{C T}$ =0

Xem đáp án

Giá trị cực đại của hàm số là 5.

Chọn A.

Câu 14:

13/07/2024

Hàm số y = f(x) liên tục trên và có bảng xét dấu đạo hàm như hình vẽ. Hỏi hàm số y = f(2x +1) có bao nhiêu điểm cực trị?

A. 3

B. 2

C. 1

D. 4

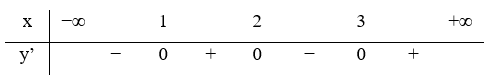
Xem đáp án

Chọn

$f^{'} (x) = (x - 1) (x - 2) (x - 3)$

$\Rightarrow f^{'} (2 x + 1) = 2 x . (2 x - 2) . (2 x - 3)$

Ta có

$y^{'} = 2 f^{'} (2 x + 1) = 4 x . (2 x - 2) . (2 x - 3);$

$y^{'} = 0 \Leftrightarrow x = \{0; 1; \frac{3}{2}\}$

Vậy hàm số đã cho có 3 điểm cực trị.

Chọn A.

Câu 15:

22/07/2024

Tìm giá trị lớn nhất của hàm số $[1; 3] .$

Xem đáp án

Đạo hàm:

$f' (x) = 3 x^{2} - 4 x - 4$

$\to f' (x) = 0$

$\Leftrightarrow [\begin{array}{l} x = 2 \in [1; 3] \\ x = - \frac{2}{3} \notin [1; 3] \end{array}$

Ta có:

$\{\begin{matrix} f (1) = - 4 \\ f (2) = - 7 \\ f (3) = - 2 \end{matrix}$

$\to \underset{[1; 3]}{m a x} f (x) = - 2$

Chọn B.

Cách 2. Sử dụng chức năng MODE 7 và nhập hàm $f (x) = x^{3} - 2 x^{2} - 4 x + 1$ với thiết lập Start 1, End 3, Step 0.2.

Quan sát bảng giá trị F(x) ta thấy giá trị lớn nhất F(x) bằng -2 khi x = 3

Câu 16:

12/07/2024

Tìm tập giá trị T của hàm số $x \in [3; 5]$ .

Xem đáp án

Đạo hàm:

$\forall x \in (3; 5)$ .

Suy ra hàm số đồng biến trên $[3; 5]$ nên

$\min_{[3; 5]} f (x) = f (3) = \frac{29}{3};$

$\max_{[3; 5]} f (x) = f (5) = \frac{127}{5}$

Vậy tập giá trị của hàm số là đoạn $[\frac{29}{3}; \frac{127}{5}] .$

Chọn C.

Câu 17:

18/07/2024

Tìm giá trị lớn nhất M của hàm số $[- 6; 6]$

A. M = 0

B. M = 9

C. M = 55

D. M = 110

Xem đáp án

Xét hàm số g(x) = - x² – 4x + 5 liên tục trên đoạn [-6; 6].

Đạo hàm:

$g' (x) = - 2 x - 4$

$\overset{}{\to} g' (x) = 0$

$\Leftrightarrow x = - 2 \in [- 6; 6] .$

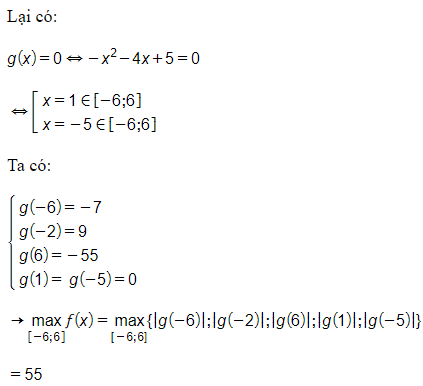
Chọn C.

Nhận xét. Bài này rất dễ sai lầm vì không để ý hàm trị tuyệt đối không âm.

Câu 18:

23/07/2024

Cho hàm số $[- 2; 3]$ bằng:

A. 2.

B. 3.

C. 4.

D. 5.

Xem đáp án

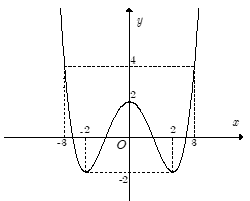
Nhận thấy trên đoạn [-2;3] đồ thị hàm số có điểm cao nhất có tọa độ (3;4)

$\to$ giá trị lớn nhất của hàm số này trên đoạn [-2;3] bằng 4

Chọn C.

Câu 19:

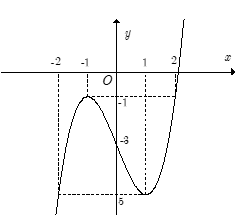
21/07/2024

Cho hàm số $[- 2; 2]$ .

A. m=−5, M=0

B. m=−5, M=−1

C. m=−1, M=0

D. m=−2, M=2

Xem đáp án

Nhận thấy trên đoạn $[- 2; 2]$

● Đồ thị hàm số có điểm thấp nhất có tọa độ (-2;-5) và (1;-5)

$\to$ giá trị nhỏ nhất của hàm số này trên đoạn [-2;2] bằng -5

● Đồ thị hàm số có điểm cao nhất có tọa độ (-1;-1) và (2;-1)

$\to$ giá trị lớn nhất của hàm số này trên đoạn [-2;2] bằng -1

Chọn B.

Câu 20:

23/07/2024

Đồ thị hàm số $y = a x^{3} + b x^{2} + c x + 1$ có đồ thị như hình vẽ sau.

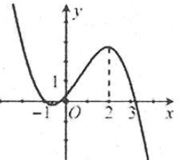
Mệnh đề nào dưới đây đúng?

A. a<0;b>0;c>0;d>0

B. a<0;b<0;c<0;d>0

C. a<0;b<0;c>0;d>0

D. a<0;b>0;c<0;d>0a<0;b>0;c<0;d>0

Xem đáp án

Ta có:

$\lim_{x \to + \infty} y = - \infty$ ,

$\lim_{x \to - \infty} y = + \infty \Rightarrow a < 0$

Đồ thị cắt trục tung tại điểm có tung độ dương $\Rightarrow d > 0$ .

Ta có: $\Rightarrow \frac{c}{a} < 0 \Rightarrow c > 0$ .

Chọn A.

Câu 21:

21/07/2024

Cho hàm số $y = a x^{4} + b x^{2} + c$ có đồ thị như hình vẽ bên.

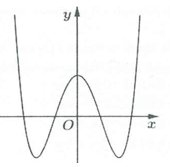
Mệnh đề nào dưới đây là đúng?

A. a>0,b<0,c<0

B. a<0,b>0,c>0

C. a>0,b>0,c>0

D. a>0,b<0,c>0

Xem đáp án

Ta có $\lim_{x \to + \infty} y = + \infty$ do đó a > 0

Đồ thị hàm số có 3 điểm cực trị nên $a b < 0 \Rightarrow b < 0$

Đồ thị hàm số cắt trục tung tại điểm $(0; c)$ nên c > 0.

Chọn D.

Câu 22:

13/07/2024

Cho hàm số $f (x) = 2 m$ có đúng hai nghiệm phân biệt.

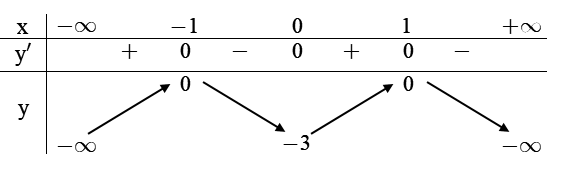
Xem đáp án

Để phương trình $f (x) = 2 m$ có hai nghiệm phân biệt thì

$[\begin{array}{l} 2 m = 0 \\ 2 m < - 3 \end{array} \Leftrightarrow [\begin{array}{l} m = 0 \\ m < - \frac{3}{2} \end{array}$ .

Chọn C.

Câu 23:

20/07/2024

Tiếp tuyến của đồ thị hàm số $y = - \frac{1}{9} x$ là

Xem đáp án

Ta có $M (a; a^{3} - 3 a + 2)$ là tọa độ tiếp điểm

Hệ số góc là

$k = y^{'} (a) = 3 a^{2} - 3 = 9$

$\Leftrightarrow a^{2} = 4$

$\Leftrightarrow [\begin{array}{l} a = 2 \Rightarrow M (2; 4) \Rightarrow y = 9 x - 14 \\ a = - 2 \Rightarrow M (- 2; 0) \Rightarrow y = 9 x + 18 \end{array}$

Chọn C.

Câu 24:

23/07/2024

Cho hàm số $y = \frac{2}{1 - x}$ có đồ thị hàm số (C). Viết phương trình tiếp tuyến của (C) tại giao điểm của (C) và trục tung.

A. y=2x+2

B. y=x+2

C. y=−2x+2

D. y=2x−2

Xem đáp án

Ta có $y^{'} = \frac{2}{{(1 - x)}^{2}}$ .

Giao điểm với trục tung là $y^{'} (0) = 2$

Phương trình tiếp tuyến là $y = 2 x + 2$ .

Chọn A.

Câu 25:

21/07/2024

Phương trình tiếp tuyến của đồ thị hàm số $A (3; 1)$ là:

A. y=−9x−26

B. y=9x−26

C. y=−9x−3

D. y=9x+2

Xem đáp án

Ta có $y^{'} = 3 x^{2} - 6 x$ .

Hệ số góc là $y = 9 x - 26$ .

Chọn B.

Câu 26:

17/07/2024

Cho đồ thị hàm số $y = \frac{1}{3} x^{3} - 2 x^{2} + 3 x$ . Phương trình nào dưới đây là phương trình tiếp tuyến hệ số góc nhỏ nhất của đồ thị trên.

Xem đáp án

Ta có:

$y^{'} = x^{2} - 4 x + 3$

$= {(x - 2)}^{2} - 1 \geq - 1$

khi $x = 2 \Rightarrow y = \frac{2}{3}$

Phương trình tiếp tuyến là:

$y = - (x - 2) + \frac{2}{3} = - x + \frac{8}{3}$ .

Chọn A.

Câu 27:

12/07/2024

Cho hàm số $Δ : y = 3 x + 2018$ .

A. m= $\frac{7}{3}$

B. m = 1

C. m = 2

D. m=− $\frac{1}{3}$

Xem đáp án

Hệ số góc của tiếp tuyến tại điểm $x = x_{0}$ là

$k = y^{'} (x_{0}) = 3 x_{0}^{2} - 4 x_{0} + m - 1$

Ta có:

$3 x_{0}^{2} - 4 x_{0} + 1$

$= 3 {(x_{0} - \frac{2}{3})}^{2} - \frac{1}{3} \geq - \frac{1}{3}$

$\Rightarrow k \geq m - \frac{4}{3}$ .

Do đó $k_{\min} = m - \frac{4}{3}$

Theo bài ra, ta có:

$3 k_{\min} = - 1$

$\Leftrightarrow 3 (m - \frac{4}{3}) = - 1$

$\Leftrightarrow m - \frac{4}{3} = - \frac{1}{3}$

$\Leftrightarrow m = 1$

Chọn B.

Câu 28:

23/07/2024

Gọi S là tập hợp các giá trị của hàm số m sao cho đường thẳng $I (1; - 3)$ mà tiếp tuyến với tại A và tại B vuông góc với nhau. Tính tổng các phần tử của S.

A. -1

B. 1

C. 2

D. 5

Xem đáp án

Phương trình hoành độ giao điểm là:

$2 x^{3} - 3 x^{2} - 2 = m x - m - 3$

$\Leftrightarrow 2 x^{3} - 3 x^{2} + 1 - m (x - 1) = 0$

$\Leftrightarrow (x - 1) (2 x^{2} - x - 1) - m (x - 1) = 0$

$\Leftrightarrow (x - 1) (2 x^{2} - x - 1 - m) = 0$

$\Leftrightarrow [\begin{array}{l} x = 1 \Rightarrow y = - 3 \\ g (x) = 2 x^{2} - x - 1 - m = 0 \end{array}$

Để d cắt (C) tại 3 điểm phân biệt thì $g (x) = 0$ có 2 nghiệm khác 1

$\Leftrightarrow \{\begin{cases} Δ = 1 + 8 (1 + m) > 0 \\ g (1) = - m \neq 0 \end{cases}$ (*)

Gọi $B (x_{2}; m x_{2} - m - 3)$ theo Vi-ét ta có:

$\{\begin{cases} x_{1} + x_{2} = \frac{1}{2} \\ x_{1} x_{2} = \frac{- 1 - m}{2} \end{cases}$

Để tiếp tuyến tại A và B của (C) vuông góc với nhau thì

$y^{'} (x_{1}) . y^{'} (x_{2}) = - 1$

$\Leftrightarrow (6 x_{1}^{2} - 6 x_{1}) (6 x_{2}^{2} - 6 x_{2}) = - 1$

$\Leftrightarrow x_{1} x_{2} (x_{1} - 1) (x_{2} - 1) = - \frac{1}{36}$

$\Leftrightarrow x_{1} x_{2} (x_{1} x_{2} - x_{1} - x_{2} + 1) = - \frac{1}{36}$

$= - \frac{1}{36}$

$\Leftrightarrow \frac{m^{2} + 2 m + 1}{4} - \frac{1 + m}{4} = - \frac{1}{36}$

$\Leftrightarrow m^{2} + m + \frac{1}{9} = 0$

$\Leftrightarrow m = \frac{- 3 \pm \sqrt{5}}{6} (t / m (*))$

Suy ra tổng các phần tử của S bằng -1.

Chọn A.

Lớp 1 - Cánh diều

Tiếng Anh 1

Toán lớp 1

Tiếng Việt lớp 1

Lớp 1 - Chân trời sáng tạo

Tiếng Anh 1

Toán lớp 1

Tiếng Việt lớp 1

Lớp 1 - Kết nối tri thức

Tiếng Anh 1

Toán lớp 1

Tiếng Việt lớp 1

Tiện ích

Đọc sách online

Bộ đề ôn hè lớp 1 lên lớp 2

Giáo án lớp 1

Lớp 2 - Kết nối tri thức

Toán lớp 2

Tiếng Việt lớp 2

Đạo đức lớp 2

Tự nhiên và Xã hội lớp 2

Hoạt động trải nghiệm lớp 2

Tiếng Anh lớp 2

Âm nhạc lớp 2

Lớp 2 - Cánh diều

Toán lớp 2

Tiếng Việt lớp 2

Hoạt động trải nghiệm lớp 2

Tự nhiên và Xã hội lớp 2

Tiếng Anh lớp 2

Âm nhạc lớp 2

Đạo đức lớp 2

Lớp 2 - Chân trời sáng tạo

Toán lớp 2

Tiếng Việt lớp 2

Đạo đức lớp 2

Tự nhiên và Xã hội lớp 2

Hoạt động trải nghiệm lớp 2

Tiếng Anh lớp 2

Âm nhạc lớp 2

Đề thi các môn lớp 2

Đề thi các môn lớp 2 - Kết nối tri thức

Đề thi các môn lớp 2 - Cánh diều

Đề thi các môn lớp 2 - Chân trời sáng tạo

Tiện ích

Đọc sách online

Bộ đề ôn hè lớp 2 lên lớp 3

Giáo án lớp 2

Lớp 3 - Kết nối tri thức

Toán lớp 3

Tiếng Anh lớp 3

Tiếng Việt lớp 3

Đạo đức lớp 3

Tự nhiên và Xã hội lớp 3

Hoạt động trải nghiệm lớp 3

Âm nhạc lớp 3

Tin học lớp 3

Giáo dục thể chất lớp 3

Công nghệ lớp 3

Lớp 3 - Cánh diều

Toán lớp 3

Tiếng Việt lớp 3

Tiếng Anh lớp 3

Đạo đức lớp 3

Tự nhiên và Xã hội lớp 3

Hoạt động trải nghiệm lớp 3

Âm nhạc lớp 3

Tin học lớp 3

Giáo dục thể chất lớp 3

Công nghệ lớp 3

Lớp 3 - Chân trời sáng tạo

Toán lớp 3

Tiếng Việt lớp 3

Tiếng Anh lớp 3

Đạo đức lớp 3

Tự nhiên và Xã hội lớp 3

Hoạt động trải nghiệm lớp 3

Âm nhạc lớp 3

Tin học lớp 3

Giáo dục thể chất lớp 3