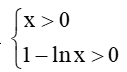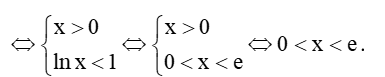Giải Toán 11 trang 26 Tập 2 Kết nối tri thức
Với giải bài tập Toán 11 trang 26 Tập 2 trong Bài tập cuối chương 6 trang 25 sách Kết nối tri thức hay nhất, chi tiết giúp học sinh dễ dàng làm bài tập Toán 11 trang 26 Tập 2.
Giải Toán 11 trang 26 Tập 2
Bài 6.35 trang 26 Toán 11 Tập 2: Cho 0 < a ≠ 1. Tính giá trị của biểu thức .
Lời giải:
Ta có:
.
Bài 6.36 trang 26 Toán 11 Tập 2: Giải các phương trình sau:
b) log3(x + 1) + log3(x + 4) = 2.
Lời giải:
a) 31 – 2x = 4x
Lấy lôgarit cơ số 3 hai vế của phương trình ta được
log331 – 2x = log34x
⇔ 1 – 2x = x log34
⇔ (2 + log34)x = 1
.
Vậy phương trình đã cho có nghiệm duy nhất là .
b) log3(x + 1) + log3(x + 4) = 2
Ta có log3(x + 1) + log3(x + 4) = 2
⇔ log3[(x + 1)(x + 4)] = 2
⇔ (x + 1)(x + 4) = 32
⇔ x2 + 5x + 4 = 9
⇔ x2 + 5x – 5 = 0
⇔ hoặc .
Loại nghiệm .
Vậy phương trình đã cho có nghiệm duy nhất là .
Bài 6.37 trang 26 Toán 11 Tập 2: Tìm tập xác định của các hàm số sau:
Lời giải:
a) Biểu thức có nghĩa khi 4x – 2x + 1 ≥ 0 ⇔ (22)x – 2x . 2 ≥ 0
⇔ (2x)2 – 2x . 2 ≥ 0 ⇔ 2x(2x – 2) ≥ 0 ⇔ 2x – 2 ≥ 0 (do 2x > 0 với mọi số thực x)
⇔ 2x ≥ 2 ⇔ x ≥ 1.
Vậy tập xác định của hàm số là D = [1; + ∞).
b) Biểu thức ln(1 – lnx) có nghĩa khi
Vậy tập xác định của hàm số y = ln(1 – lnx) là D = (0; e).
a) Nếu tỉ lệ lạm phát là 8% một năm thì sức mua của 100 triệu đồng sau hai năm sẽ còn lại bao nhiêu?
Lời giải:
a) Nếu tỉ lệ lạm phát là 8% một năm thì sức mua của 100 triệu đồng sau hai năm sẽ còn lại là (triệu đồng).
b) Ta có:
(do )
Vậy tỉ lệ lạm phát khoảng 5,13% một năm.
c) Với tỉ lệ lạm phát là 5% một năm thì với số tiền P ban đầu sau n năm sức mua còn lại là .
Vì sức mua của số tiền ban đầu chỉ còn lại một nửa nên ta có:
.
Vậy nếu tỉ lệ lạm phát là 5% một năm thì sau khoảng 14 năm sức mua của số tiền ban đầu chỉ còn lại một nửa.
trong đó r là tỉ lệ tăng trưởng vi khuẩn mỗi giờ.
Giả sử ban đầu có 500 con vi khuẩn và sau 1 giờ tăng lên 800 con. Hỏi:
a) Sau 5 giờ thì số lượng vi khuẩn là khoảng bao nhiêu con?
b) Sau bao lâu thì số lượng vi khuẩn ban đầu sẽ tăng lên gấp đôi?
Lời giải:
a) Do ban đầu có 500 con vi khuẩn và sau 1 giờ tăng lên 800 con nên N0 = 500 và với t = 1 thì N1 = 800 nên ta có: 800 = 500er ∙ 1 ⇔ er = 1,6 ⇔ r = ln1,6.
Khi đó N(t) = 500eln1,6t.
Với t = 5, ta có N(5) = 500eln1,6 ∙ 5 = 5242,88.
Vậy sau 5 giờ thì số lượng vi khuẩn khoảng 5 242 con.
b) Số lượng vi khuẩn tăng gấp đôi, tức là tăng lên 1 000 con.
Ta có: 1 000 = 500eln1,6t ⇔ eln1,6t = 2 ⇔ (eln1,6)t = 2 ⇔ 1,6t = 2 ⇔ t = log1,62 ≈ 1,47.
Vậy sau khoảng 1,47 giờ thì số lượng vi khuẩn ban đầu sẽ tăng lên gấp đôi.
a) Viết công thức tìm chữ số d nếu cho trước xác suất P.
b) Tìm chữ số có xác suất bằng 9,7% được chọn.
c) Tính xác suất để chữ số đầu tiên là 1.
Lời giải:
a) Ta có , suy ra .
b) Vì chữ số có xác suất bằng 9,7% nên P = 9,7% = 0,097, khi đó
.
Vậy chữ số có xác suất bằng 9,7% được chọn là chữ số 4.
c) Chữ số đầu tiên là 1, tức là d = 1, khi đó ta có .
Vậy xác suất để chữ số đầu tiên là 1 bằng khoảng 30,1%.
Xem thêm Lời giải bài tập Toán 11 Kết nối tri thức hay, chi tiết khác:
Xem thêm Lời giải bài tập Toán 11 Kết nối tri thức hay, chi tiết khác:
Bài 6.27 trang 25 Toán 11 Tập 2: Cho hai số thực dương x, y và hai số thực α, β tùy ý. Khẳng định nào sau đây là sai? A. xα ∙ xβ = xα + β...
Bài 6.28 trang 25 Toán 11 Tập 2: Rút gọn biểu thức ta được A. . B. . C. . D. ...
Bài 6.29 trang 25 Toán 11 Tập 2: Cho hai số thực dương a, b với a ≠ 1. Khẳng định nào sau đây là đúng? A. loga(a3b2) = 3 + logab...
Bài 6.30 trang 25 Toán 11 Tập 2: Cho bốn số thực dương a, b, x, y với a, b ≠ 1. Khẳng định nào sau đây là sai? A. loga(xy) = logax + logay...
Bài 6.31 trang 25 Toán 11 Tập 2: Đặt log25 = a, log35 = b. Khi đó, log65 tính theo a và b bằng A. . B. . C. a2 + b2. D. a + b...
Bài 6.32 trang 25 Toán 11 Tập 2: Cho hàm số y = 2x. Khẳng định nào sau đây là sai? A. Tập xác định của hàm số là ℝ...
Bài 6.33 trang 25 Toán 11 Tập 2: Hàm số nào sau đây đồng biến trên tập xác định của nó? A. y = log0,5x. B. y = e– x...
Bài 6.35 trang 26 Toán 11 Tập 2: Cho 0 < a ≠ 1. Tính giá trị của biểu thức ...
Bài 6.36 trang 26 Toán 11 Tập 2: Giải các phương trình sau: a) 31 – 2x = 4x; b) log3(x + 1) + log3(x + 4) = 2...
Bài 6.37 trang 26 Toán 11 Tập 2: Tìm tập xác định của các hàm số sau: a) ; b) y = ln(1 – lnx)...
Xem thêm Lời giải bài tập Toán 11 Kết nối tri thức hay, chi tiết khác:
Bài 18: Lũy thừa với số mũ thực
Xem thêm các chương trình khác:
- Soạn văn lớp 11 Kết nối tri thức - hay nhất
- Văn mẫu lớp 11 - Kết nối tri thức
- Tóm tắt tác phẩm Ngữ văn 11 – Kết nối tri thức
- Tác giả tác phẩm Ngữ văn 11 - Kết nối tri thức
- Giải SBT Ngữ văn 11 – Kết nối tri thức
- Bố cục tác phẩm Ngữ văn 11 – Kết nối tri thức
- Giải Chuyên đề học tập Ngữ văn 11 – Kết nối tri thức
- Nội dung chính tác phẩm Ngữ văn lớp 11 – Kết nối tri thức
- Soạn văn 11 Kết nối tri thức (ngắn nhất)
- Bài tập Tiếng Anh 11 Global success theo Unit có đáp án
- Giải sgk Tiếng Anh 11 – Global success
- Giải sbt Tiếng Anh 11 - Global Success
- Trọn bộ Từ vựng Tiếng Anh 11 Global success đầy đủ nhất
- Ngữ pháp Tiếng Anh 11 Global success
- Giải sgk Vật lí 11 – Kết nối tri thức
- Lý thuyết Vật lí 11 – Kết nối tri thức
- Giải sbt Vật lí 11 – Kết nối tri thức
- Giải Chuyên đề học tập Vật lí 11 – Kết nối tri thức
- Chuyên đề dạy thêm Vật lí 11 cả 3 sách (2024 có đáp án)
- Giải sgk Hóa học 11 – Kết nối tri thức
- Giải Chuyên đề học tập Hóa học 11 – Kết nối tri thức
- Lý thuyết Hóa 11 - Kết nối tri thức
- Giải sbt Hóa học 11 – Kết nối tri thức
- Chuyên đề dạy thêm Hóa 11 cả 3 sách (2024 có đáp án)
- Giải sgk Sinh học 11 – Kết nối tri thức
- Lý thuyết Sinh học 11 – Kết nối tri thức
- Giải Chuyên đề học tập Sinh học 11 – Kết nối tri thức
- Giải sbt Sinh học 11 – Kết nối tri thức
- Giải sgk Giáo dục Kinh tế và Pháp luật 11 – Kết nối tri thức
- Giải Chuyên đề học tập Kinh tế pháp luật 11 – Kết nối tri thức
- Lý thuyết Kinh tế pháp luật 11 – Kết nối tri thức
- Giải sbt Kinh tế pháp luật 11 – Kết nối tri thức
- Giải sgk Lịch sử 11 – Kết nối tri thức
- Giải Chuyên đề học tập Lịch sử 11 – Kết nối tri thức
- Lý thuyết Lịch sử 11 - Kết nối tri thức
- Giải sbt Lịch sử 11 – Kết nối tri thức
- Giải sgk Địa lí 11 – Kết nối tri thức
- Giải Chuyên đề học tập Địa lí 11 – Kết nối tri thức
- Lý thuyết Địa lí 11 - Kết nối tri thức
- Giải sbt Địa lí 11 – Kết nối tri thức
- Giải sgk Công nghệ 11 – Kết nối tri thức
- Lý thuyết Công nghệ 11 - Kết nối tri thức
- Giải sbt Công nghệ 11 – Kết nối tri thức
- Giải sgk Tin học 11 – Kết nối tri thức
- Giải Chuyên đề học tập Tin học 11 – Kết nối tri thức
- Lý thuyết Tin học 11 - Kết nối tri thức
- Giải sbt Tin học 11 – Kết nối tri thức
- Giải sgk Giáo dục quốc phòng an ninh 11 – Kết nối tri thức
- Lý thuyết Giáo dục quốc phòng 11 – Kết nối tri thức
- Giải sbt Giáo dục quốc phòng 11 – Kết nối tri thức
- Giải sgk Hoạt động trải nghiệm 11 – Kết nối tri thức