Giải Toán 10 trang 82 Tập 1 | Kết nối tri thức Giải Toán lớp 10

Giải Toán 10 trang 82 Tập 1

Vận dụng trang 82 Toán 10 Tập 1: Hãy tính các số đặc trưng đo xu thế trung tâm cho mẫu số liệu về điểm khảo sát của lớp A và lớp B ở đầu bài học để phân tích và so sánh hiệu quả học tập của hai phương pháp này.

Lời giải:

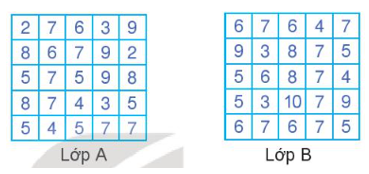
* Xét lớp A:

Bảng tần số:

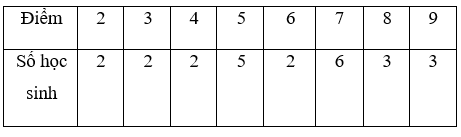
Trung bình cộng điểm khảo sát Tiếng Anh của lớp A là:

$$\begin{gathered} \frac{2.2+3.2+4.2+5.5+6.2+7.6+8.3+9.3}{2.4+5+6+3.2} \\ =\frac{148}{25}=5,92 \end{gathered}$$

Vì n = 25 nên trung vị: số thứ 13.
Ta thấy: 2 + 2 + 2 + 5 + 2 = 13.

Do đó trung vị là 6.

Từ bảng tần số, ta thấy điểm 7 xuất hiện nhiều nhất (6 lần).

Do đó mốt của số liệu là 7.

* Xét lớp B:

Bảng tần số:

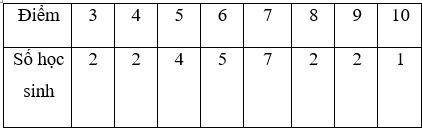
Trung bình cộng điểm khảo sát Tiếng Anh của lớp B là:

$$\begin{gathered} \frac{3.2+4.2+5.4+6.5+7.7+8.2+9.2+10.1}{2.4+4+5+7+1} \\ =\frac{157}{25}=6,28 \end{gathered}$$

Vì n = 25 nên trung vị: số thứ 13.

Ta thấy 2 + 2 + 4 + 5 = 13.

Do đó trung vị là 6.

Từ bảng tần số, ta thấy điểm 7 xuất hiện nhiều nhất (7 lần).

Do đó mốt của số liệu là 7.

Ta thấy:

+ Điểm trung bình của lớp B cao hơn điểm trung bình của lớp A (vì 6,28 > 5,92).

Do đó phương pháp học tập được áp dụng ở lớp B hiệu quả hơn phương pháp được áp dụng ở lớp A.

+ Số trung vị của hai dãy số liệu là bằng nhau nên nếu dùng số trung vị thì hiệu quả học tập của hai phương pháp này là như nhau.

+ Mốt của hai dãy số liệu là bằng nhau nên nếu dùng mốt thì hiệu quả học tập của hai phương pháp này là như nhau.

Bài tập

Bài 5.7 trang 82 Toán 10 Tập 1: Tìm số trung bình, trung vị, mốt và tứ phân vị của mỗi mẫu số liệu sau đây:

a) Số điểm mà năm vận động viên bóng rổ ghi được trong một trận đấu:

9        8        15      8        20

b) Giá của một số loại giày (đơn vị nghìn đồng):

350    300    650    300    450    500    300    250

c) Số kênh được chiếu của một số hãng truyền hình cáp:

36      38      33      34      32      30      34      35

Lời giải:

a) Số điểm mà năm vận động viên bóng rổ ghi được trong một trận đấu:

9        8        15      8        20

Số trung bình:

$\overline{X}=\frac{9+8+15+8+20}{5}=12$

Trung vị:

Mẫu số liệu sắp xếp theo thứ tự không giảm, ta được:

8; 8; 9; 15; 20

Ta có n = 5 là số lẻ nên trung vị là 9.

∙ Mốt:

Ta thấy số 8 là số có tần số lớn nhất (xuất hiện 2 lần).

Do đó mốt của số liệu là 8.

∙ Tứ phân vị:

+ Tìm Q₂.

Ta có trung vị là 9 nên Q₂ = 9.

+ Tìm Q₁.

Nửa số liệu bên trái là: 8 8

Trung vị của mẫu này là: (8 + 8) : 2 = 8

Do đó Q₁ = 8.

 + Tìm Q₃.

Nửa số liệu bên phải là: 15  20

Trung vị của mẫu này là: (15 + 20) : 2 = 17,5.

Do đó Q₃ = 17,5.

Vậy số trung bình là 12; trung vị là 9; mốt là 8; Q₁ = 8; Q₃ = 17,5.

b) Giá của một số loại giày (đơn vị nghìn đồng):

350    300    650    300    450    500    300    250

∙ Số trung bình:

$$\begin{gathered} \overline{X}=\frac{350+300+650+300+450+500+300+250}{8} \\ =387,5 \end{gathered}$$

∙ Trung vị:

Mẫu số liệu sắp xếp theo thứ tự không giảm ta được:

250; 300; 300; 300; 350; 450; 500; 650.

Ta có n = 8 là số chẵn nên trung vị là trung bình cộng của hai số chính giữa.

Số trung bình cộng của hai giá trị ở chính giữa là:

(300 + 350) : 2 = 325.

Do đó trung vị là 325.

∙ Mốt:

Ta thấy số 300 là số có tần số cao nhất (xuất hiện 3 lần).
Do đó mốt của dãy số liệu là 300.

∙ Tứ phân vị:

+ Tìm Q₂.

Ta có trung vị là 325.

Do đó Q₂ = 325.

+ Tìm Q₁.

Vì n chẵn nên nửa số liệu bên trái là: 250  300  300  300

Trung vị của mẫu này là: (300 + 300) : 2 = 300

Do đó Q₁ = 300.

+ Tìm Q₃.

Vì n chẵn nên nửa số liệu bên phải là: 350  450  500  650

Trung vị của mẫu này là: (450 + 500) : 2 = 475

Do đó Q₃ = 475.

Vậy số trung bình là 387,5; trung vị là 325; mốt là 300; Q₁ = 300; Q₃ = 475.

c) Số kênh được chiếu của một số hãng truyền hình cáp:

36  38  33  34  32  30  34  35

∙ Số trung bình:

$\overline{X}=\frac{36+38+33+34+32+30+34+35}{8}=34$

∙ Trung vị:

Sắp xếp theo thứ tự không giảm: 30  32  33  34  34  35  36  38

Ta có n = 8 là số chẵn nên trung vị là trung bình cộng của hai số chính giữa.

Hai số chính giữa là 34 và 34.

Do đó trung vị là: (34 + 34) : 2 = 34.

∙ Mốt:

Ta thấy số 34 là số có tần số cao nhất (xuất hiện 2 lần).

Do đó mốt của dãy số liệu là 34.

∙ Tứ phân vị:

+ Tìm Q₂.

Ta có trung vị là 34.

Do đó Q₂ = 34.

+ Tìm Q₁.

Vì n chẵn nên nửa số liệu bên trái là: 30  32  33  34

Trung vị của mẫu này là: (32 + 33) : 2 = 32,5

Do đó Q₁ = 32,5.

+ Tìm Q₃.

Vì n chẵn nên nửa số liệu bên phải là: 34  35  36  38

Trung vị của mẫu này là: (35 + 36) : 2 = 35,5

Do đó Q₃ = 35,5.

Vậy số trung bình là 34; trung vị là 34; mốt là 34; Q₁ = 32,5; Q₃ = 35,5.

Bài 5.8 trang 82 Toán 10 Tập 1: Hãy chọn số đặc trưng đo xu thế trung tâm của mỗi mẫu số liệu sau. Giải thích và tính giá trị của số đặc trưng đó.

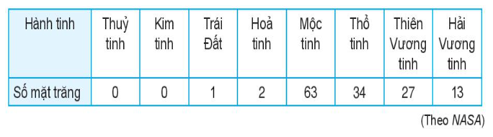
a) Số mặt trăng đã biết của các hành tinh:

b) Số đường chuyền thành công trong một trận đấu của một số cầu thủ bóng đá:

32   24   20   14   23.

c) Chỉ số IQ của một nhóm học sinh:

80   102   83   103   108   94   110   106   104   100.

d) Các sai số trong một phép đo:

10   15   18   15   14   13   42   15   12   14   42.

Lời giải:

a) Sắp xếp lại số liệu:

0   0   1   2   13   27   34   63

Mẫu số liệu đã cho có số liệu tăng dần, do đó ta nên dùng số trung bình để đo xu thế trung tâm của mẫu số liệu này.

Số trung bình của mẫu số liệu là:

$\overline{x}=\frac{0+0+1+2+13+27+34+63}{8}=17,5$.

Ta không dùng trung vị vì M_e = (2 + 13) : 2 = 7,5, giá trị này chênh lệch nhiều so với các số liệu ở nửa bên phải.

b) Các số liệu bài cho không chênh lệch quá lớn với nhau nên ta chọn số trung bình làm số đặc trưng đo xu thế trung tâm.

Số đường chuyền trung bình là:

$\frac{32+24+20+14+23}{5}=22,6$.

c) Các số liệu bài cho không chênh lệch quá lớn với nhau nên ta chọn số trung bình làm số đặc trưng đo xu thế trung tâm.

Chỉ số IQ trung bình của nhóm học sinh là:

$\frac{80+102+83+103+108+94+110+106+104+100}{10}=99.$

d) Mẫu số liệu đã cho có đa số các sai số là giống nhau, riêng giá trị 42 lớn hơn hẳn các giá trị khác, đây được xem là giá trị bất thường nên ta chọn số trung vị là số đặc trưng đo xu thế trung tâm của mẫu số liệu đã cho.

Sắp xếp dãy số liệu đã cho theo thứ tự không giảm ta được:

10; 12; 13; 14; 14; 15; 15; 15; 18; 42; 42

Vì dãy số liệu có 11 số nên trung vị của mẫu là M_e = 15.

Xem thêm lời giải bài tập Toán lớp 10 Kết nối tri thức với cuộc sống hay, chi tiết khác: 

Giải Toán 10 trang 78 Tập 1

Giải Toán 10 trang 79 Tập 1

Giải Toán 10 trang 80 Tập 1

Giải Toán 10 trang 81 Tập 1

Giải Toán 10 trang 83 Tập 1