Giải SBT Toán 6 (Kết nối tri thức): Ôn tập Chương 2

Giải SBT Toán 6 Ôn tập Chương 2

Câu hỏi (Trắc nghiệm)

Bài 1 trang 45 sách bài tập Toán 6 Tập 1 - KNTT: Khẳng định nào trong các khẳng định sau là sai?

(A) Một số chia hết cho 9 thì luôn chia hết cho 3;

(B) Nếu hai số đều chia hết cho 9 thì tổng của hai số đó cũng chia hết cho 9;

(C) Nếu hai số đều không chia hết cho 9 thì tổng của hai số đó cũng không chia hết cho 9;

(D) Một số chẵn thì luôn chia hết cho 2.

Lời giải.

Xét đáp án C.

Ta lấy 1 ví dụ hai số đều không chia hết cho 9 là: 2 và 16

Nhưng tổng hai số là 2 + 16 = 18 chia hết cho 9.

Do đó khẳng định (C) là sai.

Đáp án cần chọn là: C

Bài 2 trang 45 sách bài tập Toán 6 Tập 1 - KNTT: Số nào trong các số sau là số nguyên tố?

(A) 2 020;                 

(B) 1 143;                 

(C) 3 576;                  

(D) 461.

Lời giải.

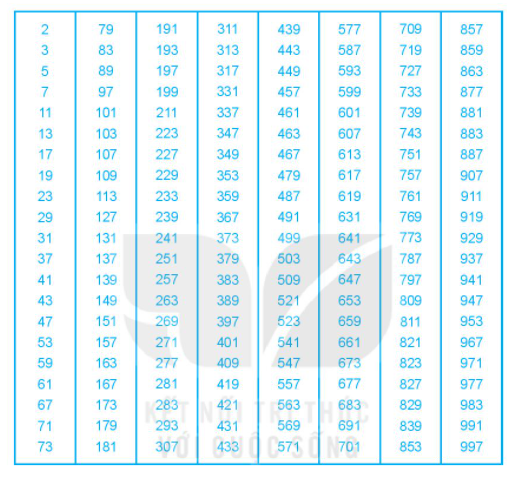
Cách 1: Tra bảng số nguyên tố nhỏ hơn 1000 ta thấy 461 là số nguyên tố.

Cách 2:

(A) Vì 2 020 có chữ số tận cùng là 0 nên  do đó 2 020 là hợp số.

(B) Vì 1 143 có tổng các chữ số 1 + 1 + 4 + 3 = 9, vì  nên 1 143 là hợp số.

(C) Vì 3 576 có tổng các chữ số 3 + 5 + 7 + 6 = 21, vì  nên 3 576 là hợp số.

Đáp án cần chọn là: D

Bài 3 trang 45 sách bài tập Toán 6 Tập 1 - KNTT: Số nào trong các số sau không là số nguyên tố?

(A) 17;                     

 (B) 97;                      

(C) 2 335;                 

(D) 499.

Lời giải.

Vì 2 335 có chữ số tận cùng là 5 nên 2 335 chia hết cho 5. Nên ngoài hai ước là 1 và 2 335 còn có thêm ước là 5. Do đó 2 335 không là số nguyên tố.

Đáp án cần chọn là: C

Bài 4 trang 45 sách bài tập Toán 6 Tập 1 - KNTT: Trong các số sau, số nào chia hết cho 9?

(A) 2 549;                  

(B) 1 234;                  

(C) 7 895;                 

(D) 9 459.

Lời giải.

(A). 2 549 có tổng các chữ số 2 + 5 + 4 + 9 = 20  nên 2 549

(B). 1 234 có tổng các chữ số 1 + 2 + 3 + 4 = 10  nên 1 234

(C). 7 895 có tổng các chữ số 7 + 8 + 9 + 5 = 29  nên 7 895

(D) 9 459 có tổng các chữ số 9 + 4 + 5 + 9 = 27  nên 9 459

Đáp án cần chọn là: D

Bài 5 trang 45 sách bài tập Toán 6 Tập 1 - KNTT: Trong các số sau, số nào chia hết cho 9 nhưng không chia hết cho 5?

(A) 23 454;                 

(B) 34 515;                

(C) 54 321;              

(D) 93 240.

Lời giải.

Trong các số trên các số không chia hết cho 5 là: 23 454 và 54 321 vì không có chữ số tận cùng là 0 hoặc 5.

+) 23 454 có tổng các chữ số 2 + 3 + 4 + 5 + 4 = 18  nên 23 454

+) 54 321 có tổng các chữ số 5 + 4 + 3 + 2 + 1 = 15  nên 54 321

Đáp án cần chọn là: A

Bài 6 trang 45 sách bài tập Toán 6 Tập 1 - KNTT: Trong các khẳng định sau, khẳng định nào sai?

(A) Ước chung của hai số tự nhiên a và b là ước của ước chung lớn nhất của chúng;

(B) Bội chung của hai số tự nhiên a và b là bội của bội chung nhỏ nhất của chúng;

(C) ƯCLN(a, b) là ước của BCNN(a, b);

(D) Nếu a không chia hết cho c và b không chia hết cho c thì BCNN(a; b) cũng không chia hết cho c.

Lời giải.

(D) Ta có: 5 không chia hết cho 10

                  4 không chia hết cho 10

BCNN(4; 5) = 20 nhưng lại chia hết cho 10. Do đó khẳng định D là sai.

Đáp án cần chọn là: D

 

Bài tập

Bài 2.56 trang 45 sách bài tập Toán 6 Tập 1 - KNTT: Các tổng sau là số nguyên tố hay hợp số?

a) 2. 7. 12 + 49. 53;                                    

b) 3. 4. 5 + 2 020. 2 021. 2 022.

Lời giải.

a) Vì 7  $⋮$7 nên (2. 7. 12)  $⋮$7

            49 $⋮$ 7 nên (49. 53) $⋮$ 7

Do đó (2. 7. 12 + 49. 53) $⋮$ 7 (áp dụng tính chất chia hết của một tổng)

Nên ngoài hai ước là 1 và chính nó, tổng trên còn có thêm ước là 7.

Vậy tổng trên là hợp số.

b) Vì 4 $⋮$ 4 nên (3. 4. 5) $⋮$ 4

            2 020 $⋮$ 4 nên (2 020. 2 021. 2 022) $⋮$ 4

Do đó (3. 4. 5 + 2 020. 2 021. 2 022) $⋮$ 4 (áp dụng tính chất chia hết của một tổng)

Nên ngoài hai ước là 1 và chính nó, tổng trên còn có thêm ước là 4.

Vậy tổng trên là hợp số.

Bài 2.57 trang 45 sách bài tập Toán 6 Tập 1 - KNTT: Thực hiện phép tính rồi phân tích kết quả ra thừa số nguyên tố:

a) ${12}^2:6+2.7$;                                 

b) ${5.4}^2-36:3^2$

Lời giải.

a)${12}^2:6+2.7$

= 144: 6 + 14

= 24 + 14

= 38

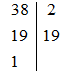
Vậy 38 = 2. 19

b) ${5.4}^2-36:3^2$       

= 5. 16 – 36: 9

= 80 – 4

= 76

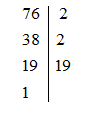
Vậy    $76=2^2.19$

Bài 2.58 trang 45 sách bài tập Toán 6 Tập 1 - KNTT: Số học sinh khối lớp 6 của một trường trong khoảng từ 200 đến 300 học sinh, khi xếp thành các hàng 10; 12 và 15 người đều thừa 5 em. Tính số học sinh khối lớp 6.

Lời giải.

Gọi x là số học sinh khối lớp 6 của trường (học sinh; $x\in {\mathbb{N}}^{*}$, $200\le x\le 300$)

Khi xếp thành hàng 10 thừa 5 em thì x chia 10 dư 5 hay (x – 5) $⋮$ 10

Khi xếp thành hàng 12 thừa 5 em thì x chia 12 dư 5 hay (x – 5) $⋮$ 12

Khi xếp thành hàng 15 thừa 5 em thì x chia 15 dư 5 hay (x – 5) $⋮$ 15

Do đó (x – 5) là bội chung của 10; 12 và 15

Ta có: 10 = 2. 5;                 12 = $2^2.3$;                         15 = 3. 5

BCNN(10; 12; 15) =$2^2.3.5$

Khi đó (x – 5) $\in$ B(60) = {0; 60; 120; 180; 240; 300; 360;…}

Ta có bảng sau:

x – 5	0	60	120	240	300	360
x	5	65	125	245	305	365

Vì số học sinh trong trường khoảng từ 200 đến 300 học sinh nên$200\le x\le 300$ .

Do đó x = 245

Vậy số học sinh trong trường là 245 em.

Bài 2.59 trang 46 sách bài tập Toán 6 Tập 1 - KNTT: Cho A = 27 220 + 31 005 + 510. Không thực hiện phép tính, hãy xét xem A có:

a) chia hết cho 2 không?

b) chia hết cho 5 không?

c) Chia hết cho 3 không?

d) chia hết cho 9 không?

Lời giải.

a) Vì 27 220 $⋮$2; 510 $⋮$ 2 nhưng 31 005$\cancel{⋮}$2 nên tổng (27 220 + 31 005 + 510) $\cancel{⋮}$2 (áp dụng tính chất chia hết của một tổng) hay A 2

Vậy A không chia hết cho 2.

b) Vì 27 220$⋮$ 5;  31 005 $⋮$ 5;  510$⋮$ 5 nên tổng (27 220 + 31 005 + 510)  $⋮$5 (áp dụng tính chất chia hết của một tổng) hay A$⋮$  5

Vậy A chia hết cho 5.

c) Vì 31 005$⋮$ 3; 510 $⋮$3 nhưng 27 220$\cancel{⋮}$ 3 nên tổng (27 220 + 31 005 + 510) $\cancel{⋮}$ 3 (áp dụng tính chất chia hết của một tổng) hay A 3.

Vậy A không chia hết cho 3.

d) Vì A không chia hết cho 3 nên A cũng không chia hết cho 9.

Bài 2.60 trang 46 sách bài tập Toán 6 Tập 1 - KNTT: Hai số có BCNN là $2^3{.3}^4{.5}^3$ và ƯCLN là$3^2.5$ . Biết một trong hai số là $2^3{.3}^2.5$, tìm số còn lại.

Lời giải.

Ta có tích của hai số cần tìm chính là tích của ƯCLN và BCNN của hai số đó.

Gọi hai số đó là a và b.

Ta có: a. b = ƯCLN(a, b). ƯCLN(a, b)

Mà ƯCLN(a, b) = $3^2.5$; BCNN(a, b) =$2^3{.3}^4{.5}^3$

Do đó: a. b =$3^2.5$ . $2^3{.3}^4{.5}^3$= $2^3.\left(3^2{.3}^4\right).\left({5.5}^3\right)$ =$2^3{.3}^6{.5}^4$

Biết một trong hai số là $2^3{.3}^2.5$, ta giả sử a = $2^3{.3}^2.5$

Khi đó: $2^3{.3}^2.5$. b =$2^3{.3}^6{.5}^4$

                          b = ($2^3{.3}^6{.5}^4$ ): ($2^3{.3}^2.5$ )

                          b =$(2^3:2^3).(3^6:3^2).(5^4:5)$

                           b =        $3^{6-2}{.5}^{4-1}$                           

                           b =$3^4{.5}^3$

Vậy số còn lại là $3^4{.5}^3$.

Bài 2.61 trang 46 sách bài tập Toán 6 Tập 1 - KNTT: Nếu ta nhân số 12 345 679 với một số a bất kì có một chữ số, rồi nhân kết quả đó với 9 thì ta được số có 9 chữ số, mỗi chữ số đều là a, chẳng hạn khi a = 3 thì 12 345 679. 3 = 37 037 037; 37 037 037. 9 = 333 333 333. Em hãy giải thích tại sao.

Lời giải.

Ta nhân số 12 345 679 với một số a bất kì có một chữ số, rồi nhân kết quả đó với 9, ta được: 12 345 679. a. 9 = (12 345 679. 9). a

+) Ta có: 12 345 679. 9 = 12 345 679. (10 – 1) = 12 345 679. 10 - 12 345 679. 1

 = 123 456 790 – 12 345 679 = 111 111 111

Do đó: 12 345 679. a. 9 = (12 345 679. 9). a = 111 111 111. a = $\overline{aaa\text{\hspace{0.17em}aa}a\text{\hspace{0.17em}aa}a}$(do a có một chữ số)

Bài 2.62 trang 46 sách bài tập Toán 6 Tập 1 - KNTT: Tìm các số tự nhiên n sao cho $6⋮(n+1)$.

Lời giải.

Vì nên (n + 1) $\in$ Ư(6) = {1; 2; 3; 6}

Ta có bảng sau:

n + 1	1	2	3	6
n	0	1	2	5

Vì n là số tự nhiên nên n $\in$ {0; 1; 2; 5}

Vậy n $\in$ {0; 1; 2; 5}.

Bài 2.63 trang 46 sách bài tập Toán 6 Tập 1 - KNTT: Biết hai số $2^3{.3}^a$  và  $2^b{.3}^5$có ước chung lớn nhất là $2^2{.3}^5$ và bội chung nhỏ nhất là $2^3{.3}^6$. Hãy tìm giá trị của các số tự nhiên a và b.

Lời giải.

Gọi x =  $2^3{.3}^a$và y =$2^b{.3}^5$

Ta có tích của hai số là tích của ƯCLN và BCNN của hai số đó.

Ta có: x. y = ƯCLN(x, y). BCNN(x, y)

Vì ước chung lớn nhất của hai số là $2^2{.3}^5$ và bội chung nhỏ nhất của hai số là$2^3{.3}^6$ 

Do đó: $2^3{.3}^a$.$2^b{.3}^5$  = $2^2{.3}^5$.$2^3{.3}^6$

      $\left(2^3{.2}^b\right).\left(3^a{.3}^5\right)$   =$\left(2^2{.2}^3\right).\left(3^5{.3}^6\right)$

             $2^{3+b}{.3}^{a+5}$     =$2^{2+3}{.3}^{5+6}$

                 $2^{3+b}{.3}^{a+5}$     =$2^5{.3}^{11}$

Vì thế 3 + b = 5. Suy ra b = 5 – 3 = 2

           a + 5 = 11. Suy ra a = 11 – 5 = 6

Vậy a = 6; b = 2.

Bài 2.64 trang 46 sách bài tập Toán 6 Tập 1 - KNTT: Thực hiện các phép tính sau:

a) $\frac{9}{14}+\frac{8}{21}$;                              

b) $\frac{13}{15}-\frac{7}{12}$

Lời giải.

a) Ta có 14 = 2. 7;    21 = 3. 7

BCNN(14, 21) = 2. 3. 7 = 42

Ta có thể chọn mẫu chung của hai phân số $\frac{9}{14};\frac{8}{21}$ là 42

Khi đó:

$\frac{9}{14}=\frac{9.3}{14.3}=\frac{27}{42}$;           $\frac{8}{21}=\frac{8.2}{21.2}=\frac{16}{42}$                 

Vậy $\frac{9}{14}+\frac{8}{21}=\frac{27}{42}+\frac{16}{42}=\frac{27+16}{42}=\frac{43}{42}$

b)

Ta có: 15 = 3. 5;                12 =$2^2.3$

BCNN(15, 12) =  = 60

Ta có thể chọn mẫu chung của hai phân số $\frac{13}{15};\frac{7}{12}$ là 60

Khi đó:

$\frac{13}{15}=\frac{13.4}{15.4}=\frac{52}{60}$;       $\frac{7}{12}=\frac{7.5}{12.5}=\frac{35}{60}$                    

Vậy $\frac{13}{15}-\frac{7}{12}=\frac{52}{60}-\frac{35}{60}=\frac{52-35}{60}=\frac{17}{60}$.

 

Xem thêm lời giải sách bài tập Toán lớp 6 sách Kết nối tri thức hay, chi tiết khác:

Bài 13: Tập hợp các số nguyên

Bài 14: Phép cộng và phép trừ số nguyên

Bài 15: Quy tắc dấu ngoặc

Bài 16: Phép nhân số nguyên

Bài 17: Phép chia hết. Ước và bội của một số nguyên

Xem thêm tài liệu Toán lớp 6 sách Kết nối tri thức hay, chi tiết khác:

Lý thuyết Bài tập cuối chương 2

Trắc nghiệm Bài: ôn tập chương 2