Giải SBT Toán 6 (Kết nối tri thức): Ôn tập Chương 9

Giải SBT Toán 6 Ôn tập Chương 9

Câu hỏi (Trắc nghiệm)

Bài 1 trang 88 sách bài tập Toán 6 Tập 2 - KNTT: Mai nói rằng: “Dữ liệu là số được gọi là số liệu”. Theo em, Mai nói thế đúng hay sai?

A. Đúng

B. Sai

Lời giải:

Dữ liệu là số hay trong dữ liệu ấy, có dữ liệu là số thì được gọi là số liệu.

Do đó, Mai nói đúng.

Vậy chọn A. Đúng.

Bài 2 trang 88 sách bài tập Toán 6 Tập 2 - KNTT: Linh đo nhiệt độ cơ thể (đơn vị ^oC) của 5 bạn trong lớp thu được dãy số liệu sau:

37          

36,9        

37,1         

36,8         

36,9.

Linh dã dùng phương pháp nào để thu thập số liệu trên?

A. Quan sát

B. Làm thí nghiệm

C. Lập bảng hỏi

D. Phỏng vấn

Lời giải:

Linh đã tiến hành làm thí nghiệm đo nhiệt độ cơ thể của 5 bạn trong lớp để thu được dãy số liệu trên.

Vậy Linh dã dùng phương pháp để thu thập số liệu trên là: B. Làm thí nghiệm.

Bài 3 trang 88 sách bài tập Toán 6 Tập 2 - KNTT: Trong biểu đồ tranh cần chỉ rõ mỗi biểu tượng biểu diễn bao nhiêu đối tượng.

Khẳng định trên là đúng hay sai?

A. Đúng

B. Sai

Lời giải:

Trong biểu đồ tranh cần chỉ rõ mỗi biểu tượng biểu diễn bao nhiêu đối tượng là đúng.

Vậy khẳng định trên là: A. Đúng.

Bài 4 trang 88 sách bài tập Toán 6 Tập 2 - KNTT: Trong biểu đồ cột, biểu đồ cột kép, khẳng định nào sau đây không đúng?

A. Cột nào cao hơn biểu diễn số liệu lớn hơn

B. Cột nằm dưới trục ngang biểu diễn số liệu âm

C. Các cột cao như nhau biểu diễn các số liệu bằng nhau

D. Độ rộng các cột không như nhau

Lời giải:

Các khẳng định A, B, C đúng.

Khẳng định D sai vì độ rộng của các cột phải bằng nhau.

Vậy khẳng định không đúng là: D. Độ rộng các cột không như nhau.

Bài 5 trang 88 sách bài tập Toán 6 Tập 2 - KNTT: Trong một thí nghiệm thì:

A. Một kết quả có thể luôn là một sự kiện

B. Một sự kiện luôn là một kết quả có thể

Lời giải:

Khẳng định A đúng.

Khẳng định B sai vì một sự kiện có thể xảy ra hoặc không xảy ra.

Vậy trong một thí nghiệm thì: A. Một kết quả có thể luôn là một sự kiện.

Bài 6 trang 88 sách bài tập Toán 6 Tập 2 - KNTT: Xác suất thực nghiệm của một sự kiện:

A. Phụ thuộc vào số lần làm thực nghiệm

B. Không phụ thuộc vào số lần làm thực nghiệm

Lời giải:

Xác suất thực nghiệm của một sự kiện = số lần xảy ra sự kiện : Tổng số lần làm thực nghiệm.

Do đó, xác suất thực nghiệm của một sự kiện phụ thuộc vào số lần làm thực nghiệm.

Vậy chọn A. Phụ thuộc vào số lần làm thực nghiệm.

Bài tập

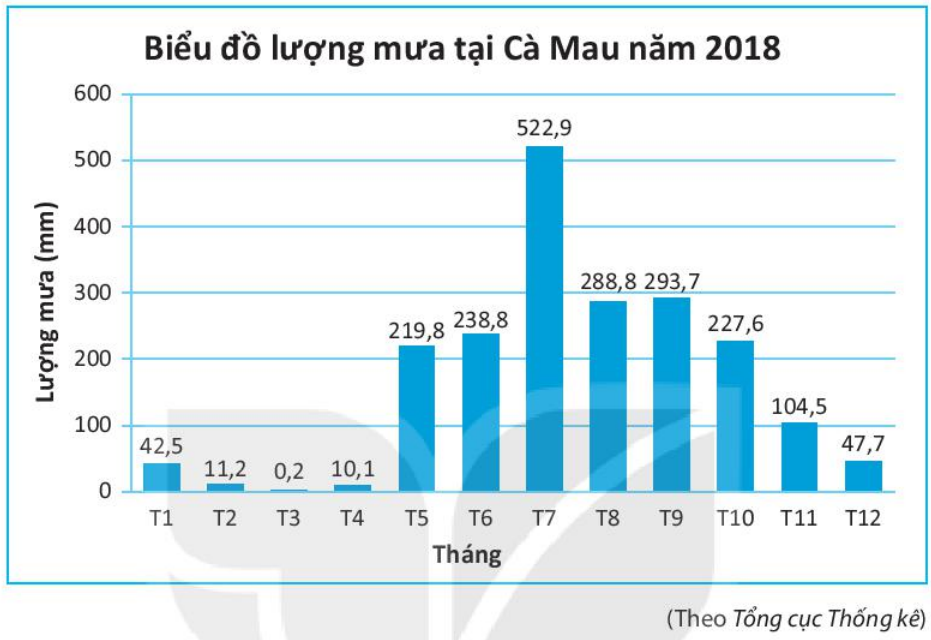
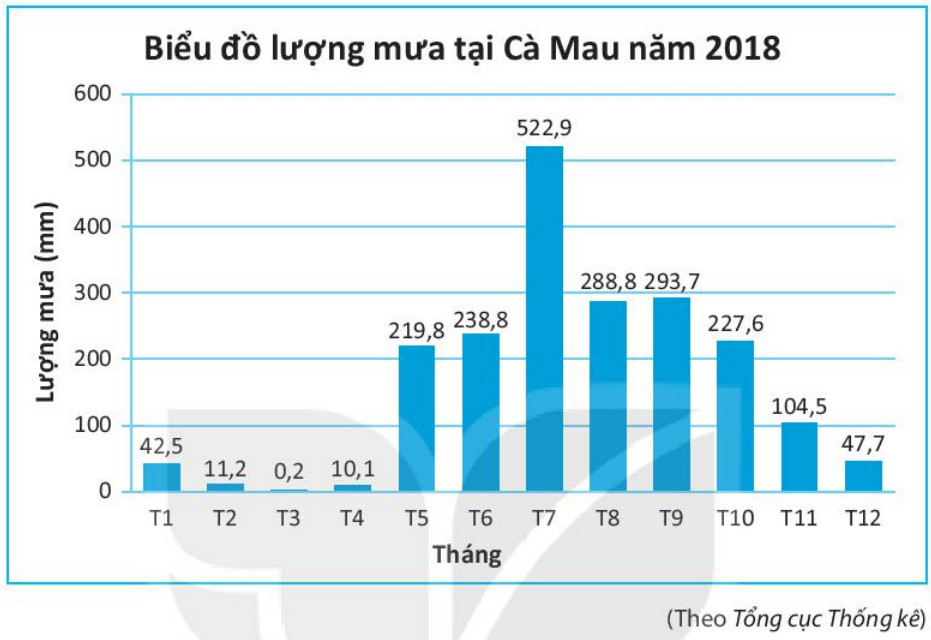
Bài 9.46 trang 89 sách bài tập Toán 6 Tập 2 - KNTT: Cho biểu đồ sau biểu diễn lượng mưa tại Cà Mau năm 2018.

a) Tính tổng lượng mưa trong năm 2018 tại Cà Mau.

b) Dự đoán 6 tháng mùa mưa là những tháng nào? Tính tổng lượng mưa trong các tháng đó.

c) Dự đoán 6 tháng mùa khô là những tháng nào? Tính tổng lượng mưa trong các tháng đó mùa khô.

Lời giải:

a) Tổng lượng mưa trong năm 2018 tại Cà Mau bằng tổng lượng của 12 tháng trong năm 2018 tại Cà Mau và bằng:

42,5 + 11,2 + 0,2 + 10,1 + 219,8 + 238,8 + 522,9 + 288,8 + 293,7 + 227,6 + 104,5 + 47,7 = 2 007,8 (mm)

Vậy tổng lượng mưa trong năm 2018 tại Cà Mau là 2 007,8 mm.

b) Dự đoán 6 tháng mùa mưa là những tháng 5; 6; 7; 8; 9; 10 vì các tháng này có lượng mưa cao nhất.

Tổng lượng mưa trong các tháng đó là:

219,8 + 238,8 + 522,9 + 288,8 + 293,7 + 227,6 = 1 791,6 (mm)

Vậy dự đoán 6 tháng mùa mưa là những tháng 5; 6; 7; 8; 9; 10 và tổng lượng mưa trong các tháng đó là 1 791,6 mm.

c) Dự đoán 6 tháng mùa khô là những tháng 11; 12; 1; 2; 3; 4 vì các tháng này có lượng mưa thấp nhất.

Tổng lượng mưa trong các tháng đó mùa khô là:

104,5 + 47,7 + 42,5 + 11,2 + 0,2 + 10,1 = 216,2 (mm)

Vậy dự đoán 6 tháng mùa khô là những tháng 11; 12; 1; 2; 3; 4 và tổng lượng mưa trong các tháng đó mùa khô là 216,2 mm.

Bài 9.47 trang 89 sách bài tập Toán 6 Tập 2 - KNTT: Hoàng quan sát được một số loại cây trong vườn nhà bà ngoại như sau:

Cây ổi, cây nhãn, cây bưởi, cây bí ngô, cây mướp, cây rau má, cây đậu ván, cây đa, cây dừa, cây cỏ mần trầu, cây đận Hà Lan, cây trầu không.

a) Trong các loại cây trên, những cây nào thuộc loại thân đứng, thân leo, thân bò?

b) Hoàn thiện bảng thống kê sau:

c) Vẽ biểu đồ cột biểu diễn bảng thống kê trên.

Lời giải:

a) - Các loại cây thân đứng là: cây ổi, cây nhãn, cây bưởi, cây đa, cây dừa, cây cỏ mần trầu.

- Các loại cây thân leo là: câu mướp, cây đậu ván, cây đậu Hà Lan, cây trầu không.

- Các loại cây thân bò là: câu bí ngô, cây rau má.

b) Dựa vào kết quả ở câu a có: 6 cây thân đứng, 4 cây thân leo và 2 cây thân bò.

Ta có bảng thống kê sau:

c) * Các bước vẽ biểu đồ cột:

Bước 1: Vẽ hai trục ngang và dọc vuông góc với nhau

- Trục ngang ghi các loại cây thân đứng, thân leo và thân bò.

- Trục dọc: ở đây giá trị lớn nhất là 6 cây (thân đứng) và nhỏ nhất là 2 cây (thân bò).

Do đó ta chia các khoảng đều nhau và đều bằng 1.

Bước 2: Tại vị trí các đối tượng trên trục ngang, vẽ các cột hình chữ nhật:

- Cách đều nhau.

- Có cùng chiều rộng.

- Có chiều cao thể hiện số cây của mỗi loại, tương ứng với khoảng chia  trên trục dọc.

Bước 3: Hoàn thiện biểu đồ

- Ghi tên biểu đồ: Một số loại cây.

- Ghi tên các trục và số liệu tương ứng trên mỗi cột:

+ Trục ngang: loại cây;

+ Trục dọc: số lượng cây.

* Biểu đồ cột biểu diễn bảng thống kê trên:

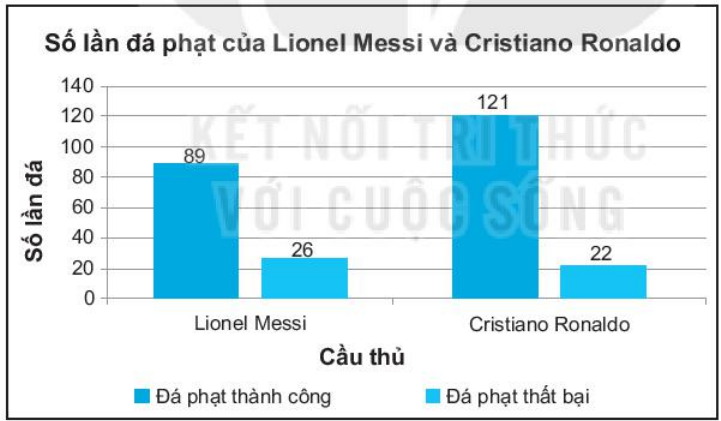
Bài 9.48 trang 89, 90 sách bài tập Toán 6 Tập 2 - KNTT: Thống kê cho thấy tính đến tháng 5-2020, Lionel Messi đã có 115 lần đá phạt đền trong đó có 89 lần thành công và 26 lần thất bại. Các số liệu tương ứng cho Cristiano Ronaldo là 143; 121; 22.

a) Vẽ biểu đồ cột kép biểu diễn số lần đá phạt đền thành công, thất bại của hai cầu thủ này.

b) Tỉ lệ đá phạt đền thành công của các cầu thủ nam là 75,57%. Hãy so sánh tỉ lệ đá phạt đền thành công của Lionel Messi và Cristiano Ronaldo với mức chung.

Lời giải:

a) * Phương pháp vẽ biểu đồ cột kép:

Bước 1: Vẽ hai trục ngang và dọc vuông góc với nhau

- Trục ngang ghi tên hai cầu thủ Lionel Messi và Cristiano Ronaldo.

- Trục dọc: căn cứ vào số lần đá phạt nhiều nhất và ít nhất.

Ta chia các khoảng đều nhau và đều bằng 20.

Bước 2: Tại vị trí từng đối tượng trên trục ngang, vẽ hai cột hình chữ nhật:

- Cách đều nhau

- Có cùng chiều rộng

- Có chiều cao thể hiện số liệu số lần đá phạt của hai cầu thủ, tương ứng với khoảng chia trên trục dọc.

Bước 3: Hoàn thiện biểu đồ.

- Tô màu hoặc gạch chéo để phân biệt hai cột trong cột kép

- Ghi tên biểu đồ: Số lần đá phạt của Lionel Messi và Cristiano Ronaldo.

- Ghi tên các trục và số liệu tương ứng trên mỗi cột:

+ Trục ngang: hai cầu thủ Lionel Messi và Cristiano Ronaldo, mỗi cầu thủ biển diễn hai cột (số lần đá phạt thành công và thất bại).

+ Trục dọc: Số lần đá.

* Ta có biểu đồ cột kép biểu diễn số lần đá phạt đền thành công, thất bại của hai cầu thủ Lionel Messi và Cristiano Ronaldo:

b) Tính tỉ lệ đá phạt đền thành công của Lionel Messi và Cristiano Ronaldo rồi so sánh với mức chung

Tỉ lệ thành công = số lần thành công : tổng số lần đá

b) Tỉ lệ đá phạt đền thành công của Lionel Messi là: $\frac{89}{115}$ ≈ 77,4%.

Tỉ lệ đá phạt đền thành công của Cristiano Ronaldo là: $\frac{121}{143}$ ≈ 84,6%

Tỉ lệ đá phạt đền thành công của các cầu thủ nam (mức chung) là 75,57%.

Vì 77,4 > 75,57 và 84,6 > 75,57 nên tỉ lệ đá phạt đền thành công của Lionel Messi và Cristiano Ronaldo đều cao hơn mức chung.

Vậy tỉ lệ đá phạt đền thành công của Lionel Messi và Cristiano Ronaldo đều cao hơn mức chung.

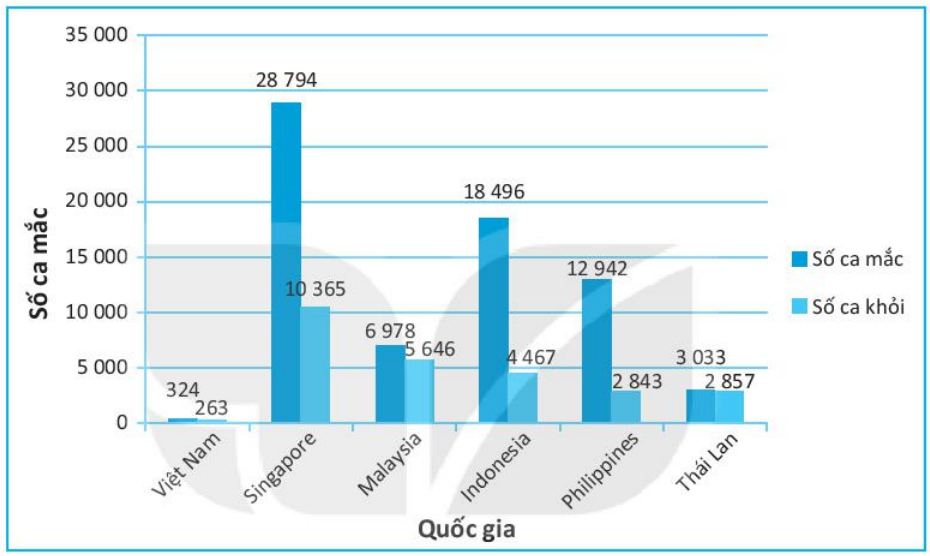
Bài 9.49 trang 90 sách bài tập Toán 6 Tập 2 - KNTT: Biểu đồ cột kép sau đây cho biết tổng số người bị mắc Covid -19 và số người đã khỏi bệnh tính đến ngày 20-5-2020 tại một số nước Đông Nam Á.

Em hãy cho biết:

a) Số lượng người mắc Covid-19 và số người khỏi bệnh ở Việt Nam là bao nhiêu?

b) Số lượng người mắc Covid-19 ở nước nào cao nhất, là bao nhiêu?

c) So sánh tỉ lệ người khỏi bệnh trong tổng số người bị mắc Covid-19 của các nước trên.

Lời giải:

Tính tỉ lệ người khỏi bệnh trong tổng số người bị mắc Covid-19 của các nước rồi so sánh.

a) Tính đến ngày 20-5-2020, số lượng người mắc Covid-19 ở Việt Nam là 324 và số người khỏi bệnh là 263.

b) So sánh chiều cao cột bên trái của các nước, ta thấy cột của bên trái (biểu diễn số ca mắc) của Singapore là cao nhất.

Vậy số lượng người mắc Covid-19 ở Singapore là cao nhất với 28 794 người.

c) Tỉ lệ người khỏi bệnh trong tổng số người bị mắc Covid-19 của Việt Nam là: $\frac{263}{324}$ ≈ 81,2%.

Tỉ lệ người khỏi bệnh trong tổng số người bị mắc Covid-19 của Singapore là:  $\frac{10365}{28794}=\frac{3455}{9598}$ ≈ 36%

Tỉ lệ người khỏi bệnh trong tổng số người bị mắc Covid-19 của Malaysia là:  $\frac{5646}{6978}=\frac{941}{1163}$  ≈ 80,9%

Tỉ lệ người khỏi bệnh trong tổng số người bị mắc Covid-19 của Indonesia là: $\frac{4467}{18496}$ ≈ 24,2%

Tỉ lệ người khỏi bệnh trong tổng số người bị mắc Covid-19 của Philippines là: $\frac{2843}{12942}$ ≈ 22%

Tỉ lệ người khỏi bệnh trong tổng số người bị mắc Covid-19 của Thái Lan là: $\frac{2857}{3033}$ ≈ 94,2%

Vì 94,2% > 81,2% > 80,9% > 36% > 24,2% > 22% nên tỉ lệ người khỏi bệnh trong tổng số người bị mắc Covid-19 được sắp xếp theo thứ tự giảm dần là: Thái Lan, Việt Nam, Malaysia, Singapore, Indonesia, Philippines.

Vậy tỉ lệ người khỏi bệnh trong tổng số người bị mắc Covid-19 được sắp xếp theo thứ tự giảm dần là: Thái Lan, Việt Nam, Malaysia, Singapore, Indonesia, Philippines với tỉ lệ tương ứng lần lượt là: 94,2%; 81,2%; 80,9%; 36%; 24,2%; 22%.

Bài 9.50 trang 90 sách bài tập Toán 6 Tập 2 - KNTT: Minh đã khảo sát về địa điểm làm bài tập ở nhà với một số bạn học sinh khối 6 với phiếu hỏi và thu được kết quả như sau:

a) Chọn biểu đồ thích hợp và vẽ biểu đồ để biểu diễn số liệu này.

b) Dựa vào kết quả khảo sát của Minh, theo em ở nhà các bạn học sinh lớp 6 hay làm bài tập ở đâu nhất. Cột nào của biểu đồ biểu diễn điều này?

Lời giải:

a) Chọn biểu đồ cột

* Các bước vẽ biểu đồ cột:

Bước 1: Vẽ hai trục ngang và dọc vuông góc với nhau.

- Trục ngang ghi danh sách các phòng.

- Trục dọc: căn cứ vào giá trị lớn nhất và giá trị nhỏ nhất. Ta chia các khoảng đều nhau và đều bằng 5.

Bước 2: Tại vị trí các đối tượng trên trục ngang, vẽ các cột hình chữ nhật

- Cách đều nhau

- Có cùng chiều rộng

- Có chiều cao thể hiện số bạn làm bài tập ở các địa điểm, tương ứng với khoảng chia  trên trục dọc.

Bước 3: Hoàn thiện biểu đồ

- Ghi tên biểu đồ: Địa điểm làm bài tập ở nhà của các học sinh khối 6.

- Ghi tên các trục và số liệu tương ứng trên mỗi cột:

+ Trục ngang: Các địa điểm

+ Trục dọc: số học sinh làm bài tập ở địa điểm đó.

Biểu đồ cột về địa điểm là bài tập về nhà của học sinh khối 6

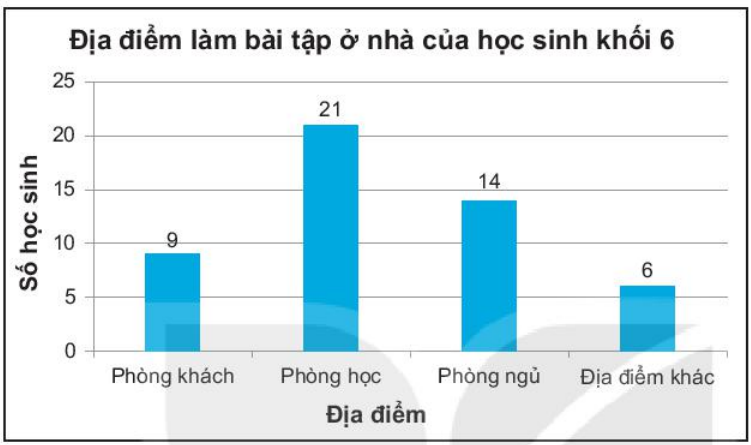
b) So sánh các phòng học ở biểu đồ trên, ta thấy cột phòng học là cao nhất.

Do đó các bạn học sinh lớp 6 làm ở phòng học là nhiều nhất.

Vậy các bạn hay làm bài tập ở phòng học nhất. Cột cao nhất trong biểu đồ biểu diễn số liệu này.

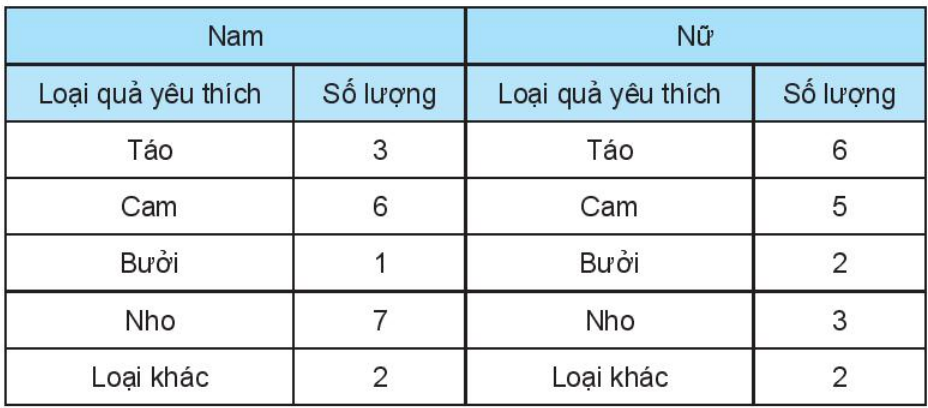
Bài 9.51 trang 91 sách bài tập Toán 6 Tập 2 - KNTT: Bình khảo sát loại quả yêu thích của các bạn trong lớp và thu được kết quả như bảng thống kê sau:

a) Em hãy giúp Bình lập phiếu khảo sát để thu được dữ liệu trong bảng thống kê trên.

b) Vẽ biểu đồ biểu diễn bảng thống kê này. Giải thích tại sao lựa chọn biểu đồ đó.

c) Loại quả nào được các bạn yêu thích nhất, được các bạn nam yêu thích nhất, được các bạn nữ yêu thích nhất?l

Lời giải:

a) Phiếu khảo sát cần có đủ mục thông tin cần thu thập.

Trong bảng trên có những thông tin cần thu thập là:

- Bạn đó là nam hay nữ?

- Loại quả mà bạn đó yêu thích nhất? (chỉ chọn một loại).

Phiếu khảo sát có thể như sau:

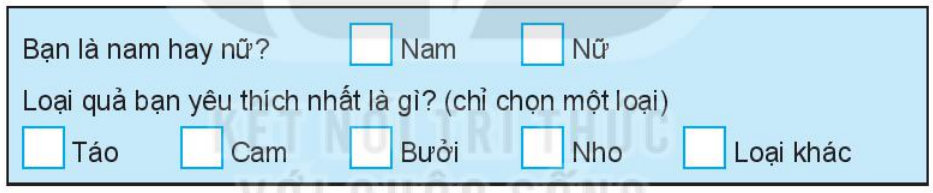
b) Ta chọn biểu đồ cột kép vì ta muốn so sánh sự yêu thích các loại quả của các bạn nam và nữ trong lớp.

* Các bước vẽ biểu đồ cột kép:

Bước 1: Vẽ hai trục ngang và dọc vuông góc với nhau

- Trục ngang ghi danh sách các loại quả

- Trục dọc: căn cứ vào giá trị lớn nhất và giá trị nhỏ nhất, ta chọn các khoảng cách đều nhau và đều bằng 2.

Bước 2: Tại vị trí từng đối tượng trên trục ngang, vẽ 2 cột hình chữ nhật

- Cách đều nhau

- Có cùng chiều rộng

- Có chiều cao thể hiện số bạn yêu thích các loại quả, tương ứng với khoảng chia trên trục dọc.

Bước 3: Hoàn thiện biểu đồ

- Tô màu hoặc gạch chéo để phân biệt hai cột trong cột kép

- Ghi tên biểu đồ: Loại quả yêu thích của các bạn.

- Ghi tên các trục và số liệu tương ứng trên mỗi cột:

+ Trục ngang: các loại quả

+ Trục dọc: số bạn yêu thích các loại quả.

* Biểu đồ thể hiện loại quả yêu thích của các bạn trong lớp như sau:

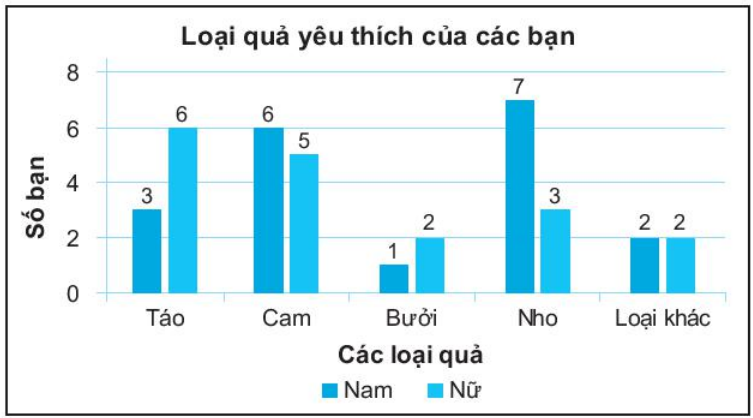
c) Cột bên trái thể hiện số bạn nam yêu thích các loại quả. Ta thấy cột bên trái của quả nho là cột cao nhất.

Do đó, các bạn nam lựa chọn quả nho nhiều nhất.

Cột bên phải thể hiện số bạn nữ yêu thích các loại quả. Ta thấy cột bên phải của quả táo là cột cao nhất.

Do đó, các bạn nữ lựa chọn quả táo nhiều nhất.

Số các bạn thích quả táo là: 3 + 6 = 9 (quả)

Số các bạn thích quả cam là: 6 + 5 = 11 (quả)

Số các bạn thích quả bưởi là: 1 + 2 = 3 (quả)

Số các bạn thích quả nho là: 7 + 3 = 10 (quả)

Số các bạn thích các loại quả khác là: 2 + 2 = 4 (quả)

Khi đó, số các bạn thích quả táo, cam, bưởi, nho, các loại khác lần lượt là: 9; 11; 3; 10; 4.

Do đó quả cam được nhiều bạn yêu thích nhất.

Vậy quả cam được các bạn yêu thích nhất, quả nho được các bạn nam yêu thích nhất, quả táo được các bạn nữ yêu thích nhất.

Bài 9.52 trang 91 sách bài tập Toán 6 Tập 2 - KNTT: Em quan tâm đến một số câu hỏi sau. Hãy cho biết bằng cách nào em có thể trả lời được các câu hỏi đó.

a) Năm quốc gia nào có diện tích lớn nhất?

b) Hoạt động yêu thích nhất của các bạn trong lớp ở kì nghỉ hè này là gì?

c) Trong lớp có bao nhiêu bạn đeo đồng hồ đeo tay đến lớp?

Lời giải:

Có nhiều cách để trả lời được các câu hỏi trên. Chẳng hạn:

a) Để trả lời được câu hỏi: “Năm quốc gia nào có diện tích lớn nhất?”, thì ta có thể tra cứu Internet.

b) Để trả lời được câu hỏi: “Hoạt động yêu thích nhất của các bạn trong lớp ở kì nghỉ hè này là gì?”, ta có thể lập bảng hỏi hoặc phỏng vấn các bạn trong lớp.

c) Để trả lời được câu hỏi: “Trong lớp có bao nhiêu bạn đeo đồng hồ đeo tay đến lớp?”, ta có thể quan sát để biết bạn nào đeo đồng hồ, bạn nào không.

Bài 9.53 trang 91, 92 sách bài tập Toán 6 Tập 2 - KNTT: Một túi đen đựng 2 quả bóng xanh, 4 quả bóng màu vàng và 1 quả bóng màu đỏ (có cùng kích thước). Nam lấy một quả bóng mà không nhìn vào túi.

a) Quả bóng Nam lấy ra có thể có màu gì?

b) Em hãy lấy một quả bóng từ túi đó 20 lần, sau mỗi lần ghi lại xem quả bóng lấy được có màu gì rồi trả bóng lại túi trước khi lấy lần sau. Hoàn thiện bảng sau:

c) Vẽ biểu đồ cột biểu diễn bảng số liệu trên.

d) Quả bóng lấy ra có màu gì là hay gặp nhất? Ít gặp nhất?

e) Tính xác suất thực nghiệm của các sự kiện sau: “Quả bóng lấy ra có màu  xanh”, “Quả bóng lấy ra có màu vàng”, “Quả bóng lấy ra có màu đỏ”.

Lời giải:

a) Nam lấy ra một quả bóng trong một túi có gồm các quả bóng có 3 màu: xanh, vàng, đỏ.

Vậy quả bóng lấy ra có thể có màu xanh, đỏ hoặc vàng.

b) Làm thí nghiệm: Một túi đen đựng 2 quả bóng xanh, 4 quả bóng màu vàng và 1 quả bóng màu đỏ (có cùng kích thước). Lấy một quả bóng từ túi đó 20 lần, sau mỗi lần ghi lại xem quả bóng lấy được có màu gì rồi trả bóng lại túi trước khi lấy lần sau.

Đối với mỗi người làm thí nghiệm sẽ có các kết quả khác nhau.

Chẳng hạn: Lấy một quả bóng từ túi đó 20 lần, ta thu được:

Em có thể tham khảo bảng sau:

c)

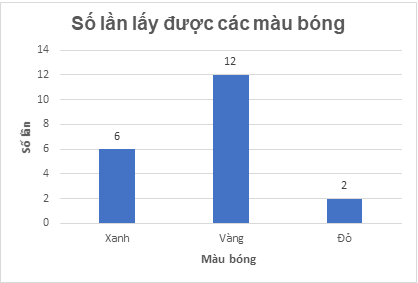
d) Các cột biểu diễn số lần lấy được các màu bóng. So sánh chiều cao các cột, ta thấy cột màu vàng cao nhất và cột màu đỏ thấp nhất.

Vậy quả bóng lấy ra có màu vàng là hay gặp nhất và màu đỏ là ít gặp nhất.

e) Xác suất thực nghiệm của sự kiện “Quả bóng lấy ra có màu xanh” là:

 =   = 30%

Xác suất thực nghiệm của sự kiện “Quả bóng lấy ra có màu vàng” là:

 =  = 60%

Xác suất thực nghiệm của sự kiện “Quả bóng lấy ra có màu đỏ” là:

  =  = 10%

Vậy xác suất thực nghiệm của các sự kiện sau: “Quả bóng lấy ra có màu  xanh”, “Quả bóng lấy ra có màu vàng”, “Quả bóng lấy ra có màu đỏ” lần lượt là: 30%; 60%; 10%.

Bài 9.54 trang 92 sách bài tập Toán 6 Tập 2 - KNTT: Em muốn tìm hiểu về đội bóng yêu thích của các bạn trong lớp. Em hãy thiết kế bảng hỏi để thực hiện mong muốn đó.

Lời giải:

Để tìm hiểu về đội bóng yêu thích của các bạn trong lớp ta có thể lập bảng hỏi để thực hiện mong muốn đó.

Ta có thể thiết kế bảng hỏi như sau (đánh dấu tích (P) vào bên phải đội bóng bạn yêu thích, nếu đội bóng yêu thích không nằm trong danh sách trên thì điền vào phần Khác:…..)

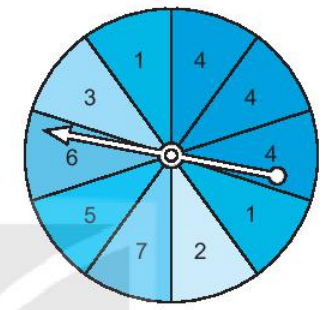
Bài 9.55 trang 92 sách bài tập Toán 6 Tập 2 - KNTT: Hà và Hoà chơi một trò chơi như sau: Họ quay một tâm bia có gán một mũi tên ở tâm (như hình vẽ). Nếu mũi tên chỉ vào số chẵn thì Hà thắng, nếu mũi tên chỉ vào số lẻ thì Hoà thắng.

a) Hà và Hoà đã chơi 30 ván thì Hà thắng 17 ván, Hoà thắng 13 ván. Tính xác suất thực nghiệm của các sự kiện “Hà thắng”, “Hoà thắng”.

b) Vẽ biểu đồ cột biểu diễn số ván thắng của Hà, Hoà.

Lời giải:

a) Xác suất thực nghiệm của các sự kiện “Hà thắng” là: 

Xác suất thực nghiệm của các sự kiện “Hoà thắng” là: 

Vậy xác suất thực nghiệm của các sự kiện “Hà thắng”, “Hoà thắng” lần lượt là 56,7% và 43,3%.

b) * Các bước vẽ biểu đồ cột:

Bước 1: Vẽ hai trục ngang và dọc vuông góc với nhau

- Trục ngang ghi hai bạn Hà và Hòa.

- Trục dọc: căn cứ vào giá trị lớn nhất và giá trị nhỏ nhất. Ta chia các khoảng cách đều nhau và đều bằng 2.

Bước 2: Vẽ các cột hình chữ nhật của các bạn Hà và Hòa, các cột có đặc điểm:

- Cách đều nhau

- Có cùng chiều rộng

- Có chiều cao thể hiện số ván thắng của mỗi bạn, tương ứng với khoảng chia  trên trục dọc.

Bước 3: Hoàn thiện biểu đồ

- Ghi tên biểu đồ: Số ván thắng trong trò chơi quay tấm bìa

- Ghi tên các trục và số liệu tương ứng trên mỗi cột:

+ Trục ngang: ghi tên hai bạn Hà và Hòa

+ Trục dọc: Số ván thắng.

Ta có biểu đồ biểu diễn số ván thắng của Hà và Hoà:

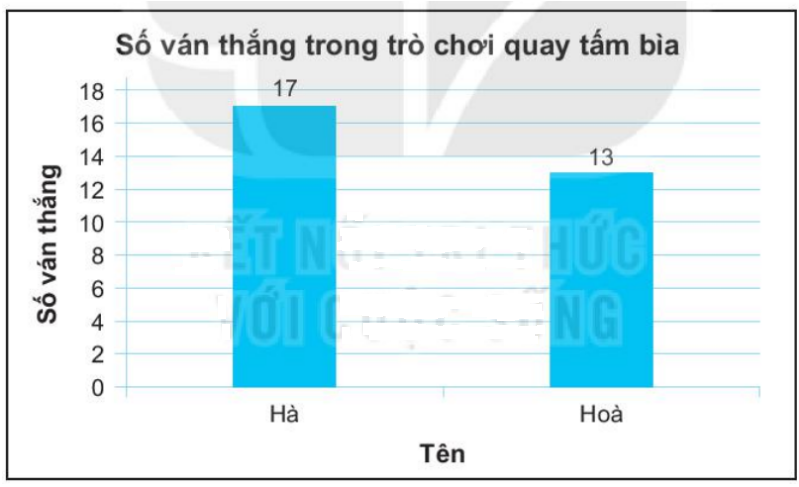
Xem thêm lời giải sách bài tập Toán lớp 6 sách Kết nối tri thức hay, chi tiết khác:

Bài 38: Dữ liệu và thu thập dữ liệu

Bài 39: Bảng thống kê và biểu đồ tranh

Bài 40: Biểu đồ cột

Bài 41: Biểu đồ cột kép

Bài 42: Kết quả có thể và sự kiện trong trò chơi, thí nghiệm