75 câu hỏi trắc nghiệm thuộc Trắc nghiệm: Tích vô hướng của hai vectơ có đáp án

Câu 1:

17/06/2026

Cho hai vectơ $\vec{a}; \vec{b}$ thỏa mãn $|\vec{a}| = 4, |\vec{b}| = 5, (\vec{a}, \vec{b}) = 120 °$ . Giá trị của tích vô hướng $\vec{a} . \vec{b}$ là:

A. 10

B. -10

C. $10 \sqrt{3}$

D. $- 10 \sqrt{3}$

Xem đáp án

$\vec{a} . \vec{b} = |\vec{a}| . |\vec{b}| . \cos (\vec{a}, \vec{b}) = 4.5. \cos 120 ° = 4.5. (- \frac{1}{2}) = - 10$

Chọn B.

Câu 2:

17/06/2026

Cho $\vec{a} = (3; - 2), \vec{b} = (5; 7)$ . Giá trị của $\vec{a} . \vec{b}$ là

A.1

B. -1

C. 29

D. -29

Xem đáp án

$\vec{a} . \vec{b} = 3.5 + (- 2) .7 = 15 - 14 = 1$ .

Chọn A.

Câu 3:

17/06/2026

Trong mặt phẳng tọa độ Oxy, cho A(2; 1), B(3; -2), C(5; 7). Giá trị của $\vec{A B} . \vec{A C}$ là

A. 15

B. 21

C. -15

D. -21

Xem đáp án

$\vec{A B} = (1; - 3), \vec{A C} = (3; 6) \Rightarrow \vec{A B} . \vec{A C} = 1.3 + (- 3) .6 = - 15$

ĐÁP ÁN C

Câu 4:

17/06/2026

Cho các vectơ $\vec{a}, \vec{b} k h á c \vec{0}$ . Khẳng định nào sau đây là đúng?

A. $\vec{a}, \vec{b}$ cùng hướng khi và chỉ khi $\vec{a} . \vec{b} = |\vec{a}| . |\vec{b}|$

B. $\vec{a}, \vec{b}$ cùng hướng khi và chỉ khi $\vec{a} . \vec{b} = - |\vec{a}| . |\vec{b}|$

C. $\vec{a}, \vec{b}$ cùng hướng khi và chỉ khi $|\vec{a} . \vec{b}| = |\vec{a}| . |\vec{b}|$

D. $\vec{a}, \vec{b}$ cùng hướng khi và chỉ khi $\vec{a} . \vec{b} = |\vec{a}| . |\vec{b}| h o ặ c \vec{a} . \vec{b} = - |\vec{a}| . |\vec{b}|$

Xem đáp án

Ta có: $\vec{a}, \vec{b} \neq \vec{0} \Rightarrow |\vec{a}| . |\vec{b}| \neq 0$

Do đó: $\vec{a} . \vec{b} = |\vec{a}| . |\vec{b}| . \cos (\vec{a}, \vec{b})$

Để $\vec{a} . \vec{b} = |\vec{a}| . |\vec{b}| \Leftrightarrow \cos (\vec{a}, \vec{b}) = 1 \Leftrightarrow (\vec{a}, \vec{b}) = 0 °$

Khi đó $\vec{a}, \vec{b}$ cùng hướng

Chọn A

Câu 5:

17/06/2026

Cho tứ giác ABCD có hai đường chéo vuông góc với nhau. Biểu thức $(\vec{A B} + \vec{B C}) . \vec{A D} - (\vec{A B} + \vec{B C}) . \vec{A B}$ bằng

A. $A B^{2}$

B. $A C^{2}$

C. $A D^{2}$

D. 0

Xem đáp án

CHỌN D.

Câu 6:

17/06/2026

Cho đoạn thẳng AB và điểm I là trung điểm của đoạn thẳng AB. M là một điểm bất kì. Khẳng định nào sau đây là đúng?

A. $\vec{M A} . \vec{M B} = M I^{2} + I A^{2}$

B. $\vec{M A} . \vec{M B} = M I^{2} - I A^{2}$

C. $\vec{M A} . \vec{M B} = 2 M I^{2} - I A^{2}$

D. $\vec{M A} . \vec{M B} = M I^{2} - 2 I A^{2}$

Xem đáp án

Do I là trung điểm của AB nên: $\vec{I A} + \vec{I B} = \vec{0}$ hay $\vec{I B} = - \vec{I A}$

$\vec{M A} . \vec{M B} = (\vec{M I} + \vec{I A}) . (\vec{M I} + \vec{I B}) = {\vec{M I}}^{2} + (\vec{I A} + \vec{I B}) . \vec{M I} + \vec{I A} . \vec{I B}$ .

$= (M I) ⃗^{2} + 0 ⃗ . (M I) ⃗ + (I A) ⃗ . (- (I A) ⃗) = 〖 M I 〗^{2} - 〖 I A 〗^{2}$

Chọn B.

Câu 7:

17/06/2026

Cho tam giác ABC có AB = 2, AC = 4, $\hat{A} = 60 °$ . M và N lần lượt là trung điểm của AB và AC. Biểu thức $\vec{B N} . \vec{C M}$ bằng

A.5

B. -5

C. 7

D. -7

Xem đáp án

$\vec{A B} . \vec{A C} = A B . A C . \cos A = 2.4. \cos 60 ° = 2.4. \frac{1}{2} = 4, {\vec{A B}}^{2} = 4, {\vec{A C}}^{2} = 16$

$\vec{B N} . \vec{C M} = (\vec{A N} - \vec{A B}) . (\vec{A M} - \vec{A C}) = (\frac{1}{2} \vec{A C} - \vec{A B}) . (\frac{1}{2} \vec{A B} - \vec{A C})$

$= \frac{1}{4} \vec{A C} . \vec{A B} - \frac{1}{2} {\vec{A B}}^{2} - \frac{1}{2} {\vec{A C}}^{2} + \vec{A C} . \vec{A B} = \frac{5}{4} \vec{A C} . \vec{A B} - \frac{1}{2} {\vec{A B}}^{2} - \frac{1}{2} {\vec{A C}}^{2}$

$= \frac{5}{4} .4 - \frac{1}{2} .4 - \frac{1}{2} .16 = - 5$

Chọn B

Câu 8:

17/06/2026

Độ dài của vectơ $\vec{a} = (5; 12)$ là

A.17

B. 169

C. 13

D. $\sqrt{159}$

Xem đáp án

$|\vec{a}| = \sqrt{5^{2} + 12^{2}} = \sqrt{169} = 13$

Chọn C

Câu 9:

17/06/2026

Cho hai vectơ $\vec{a} = (1; \sqrt{3}), \vec{b} = (- 2 \sqrt{3}; 6)$ . Góc giữa hai vectơ $\vec{a}; \vec{b}$ là

A. $0 °$

B. $30 °$

C. $45 °$

D. $60 °$

Xem đáp án

$|\vec{a}| = \sqrt{1^{2} + {(\sqrt{3})}^{2}} = 2, |\vec{b}| = \sqrt{{(- 2 \sqrt{3})}^{2} + {(6)}^{2}} = \sqrt{48} = 4 \sqrt{3}$

$\vec{a} . \vec{b} = 1. (- 2 \sqrt{3}) + \sqrt{3} .6 = 4 \sqrt{3}$

$\cos (\vec{a}, \vec{b}) = \frac{\vec{a} . \vec{b}}{|\vec{a}| |\vec{b}|} = \frac{4 \sqrt{3}}{2.4 \sqrt{3}} = \frac{1}{2} \Rightarrow (\vec{a}, \vec{b}) = 60$

Chọn D

Câu 10:

17/06/2026

Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có A(0; 2), B(-2; 8), C(-3; 1). Tọa độ tâm đường tròn ngoại tiếp của tam giác ABC là

A.( 5/2; -9/2)

B.(- 5/2; 9/2)

C.(-2; 4)

D. (-3;5)

Xem đáp án

Gọi I(a; b) là tâm đường tròn ngoại tiếp tam giác ABC.

$\{\begin{matrix} A I^{2} = B I^{2} \\ A I^{2} = C I^{2} \end{matrix} \Leftrightarrow \{\begin{matrix} {(a - 0)}^{2} + {(b - 2)}^{2} = {(a + 2)}^{2} + {(b - 8)}^{2} \\ {(a - 0)}^{2} + {(b - 2)}^{2} = {(a + 3)}^{2} + {(b - 1)}^{2} \end{matrix}$

$\Leftrightarrow \{\begin{matrix} a^{2} + b^{2} - 4 b + 4 = a^{2} + 4 a + 4 + b^{2} - 16 b + 64 \\ a^{2} + b^{2} - 4 b + 4 = a^{2} + 6 a + 9 + b^{2} - 2 b + 1 \end{matrix}$

$\{\begin{matrix} 4 a - 12 b = - 64 \\ 6 a + 2 b = - 6 \end{matrix} \Leftrightarrow \{\begin{matrix} a - 3 b = - 16 \\ 3 a + b = - 3 \end{matrix}$

$\Leftrightarrow \{\begin{matrix} a = - \frac{5}{2} \\ b = \frac{9}{2} \end{matrix}$

Chọn B.

Câu 11:

17/06/2026

Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có A(1; 1), B(4; 13), C(5; 0). Tọa độ trực tâm H của tam giác ABC là

A.(2; 2)

B. (1; 1)

C.( -2; -2)

D. (-1; -1)

Xem đáp án

$\vec{A B} = (3; 12), \vec{A C} = (4; - 1)$ $\Rightarrow \vec{A B} . \vec{A C} = 3.4 + 12 . (- 1) = 0 \Rightarrow ∆ A B C$ vuông tại A. Trực tâm của tam giác là đỉnh A. Chọn B

Câu 12:

17/06/2026

Cho hình chữ nhật ABCD có AB = 2, AD = 4, điểm M thuộc cạnh BC thỏa mãn BM = 1. Điểm N thuộc đường chéo AC thỏa mãn $\vec{A N} = x \vec{A C}$ . Giá trị của x để tam giác AMN vuông tại M là

A. 5/8

B. 5/4

C. 5/16

D. 0, 5

Xem đáp án

Chọn A.

Chú ý: Nếu có đúng bốn phương án như trong đề thi thì có thể dự đoán ngay phương án A sau khi vẽ hình

Câu 13:

17/06/2026

Cho các vectơ $\vec{a}, \vec{b} k h á c \vec{0}$ . Khẳng định nào sau đây là đúng?

A. $\vec{a} . \vec{b} = |\vec{a}| . |\vec{b}|$

B. $\vec{a} . \vec{b} = |\vec{a}| . |\vec{b}| . \sin (\vec{a}, \vec{b})$

C. $\vec{a} . \vec{b} = |\vec{a}| . |\vec{b}| . \cot (\vec{a}, \vec{b})$

D. $\vec{a} . \vec{b} = |\vec{a}| . |\vec{b}| . \cos (\vec{a}, \vec{b})$

Xem đáp án

Ta có: $\vec{a} . \vec{b} = |\vec{a}| . |\vec{b}| . c os (\vec{a}; \vec{b})$

Chọn D

Câu 14:

17/06/2026

Cho các vectơ $\vec{a}; \vec{b}$ thỏa mãn $|\vec{a}| = 8, |\vec{b}| = 10, (\vec{a}, \vec{b}) = 30 °$ . Giá trị của tích vô hướng là:

A.40

B. $- 40 \sqrt{3}$

C. $40 \sqrt{3}$

D. -40

Xem đáp án

$\vec{a} . \vec{b} = |\vec{a}| . |\vec{b}| . \cos (\vec{a}, \vec{b}) = 8.10. \cos 30 ° = 80. \frac{\sqrt{3}}{2} = 40 \sqrt{3}$

CHỌN C

Câu 15:

17/06/2026

Cho các vectơ $\vec{a}; \vec{b}$ thỏa mãn $|\vec{a}| = 4, |\vec{b}| = 6, (\vec{a}, \vec{b}) = 120 °$ Giá trị của tích vô hướng $\vec{a} . \vec{b}$

A. 12

B. -12

C. $12 \sqrt{3}$

D. $- 12 \sqrt{3}$

Xem đáp án

$\vec{a} . \vec{b} = |\vec{a}| . |\vec{b}| . \cos (\vec{a}, \vec{b}) = 4.6. \cos 120 ° = 24. \frac{- 1}{2} = - 12$

CHỌN B.

Câu 16:

17/06/2026

Cho tam giác ABC đều cạnh a. Giá trị của $\vec{A B} . \vec{A C}$ là

A. $a^{2}$

B. $\frac{1}{2} a^{2}$

C.- $\frac{1}{2} a^{2}$

D. $2 a^{2}$

Xem đáp án

$\vec{A B} . \vec{A C} = A B . A C . \cos (\vec{A B}, \vec{A C}) = a . a . \cos 60 ° = a^{2} . \frac{1}{2} = \frac{1}{2} a^{2}$

CHỌN B

Câu 17:

17/06/2026

Cho các vectơ $\vec{a}; \vec{b}$ . Khẳng định nào sau đây là đúng?

A. $(\vec{a} - \vec{b}) (\vec{a} + \vec{b}) = {|\vec{a}|}^{2} - {|\vec{b}|}^{2}$

B. ${(\vec{a} - \vec{b})}^{2} = {\vec{a}}^{2} + {\vec{b}}^{2}$

C. $(\vec{a} + \vec{b}) (\vec{a} + \vec{b}) = {\vec{a}}^{2} - {\vec{b}}^{2}$

D. $(\vec{a} + \vec{b}) (\vec{a} + \vec{b}) = {\vec{a}}^{2} + {\vec{b}}^{2}$

Xem đáp án

Ta có: $(\vec{a} - \vec{b}) . (\vec{a} + \vec{b}) = {\vec{a}}^{2} - {\vec{b}}^{2} = {|\vec{a}|}^{2} - {|\vec{b}|}^{2}$

Chọn A.

Câu 18:

17/06/2026

Cho các vectơ $\vec{a}; \vec{b}$ . Khẳng định nào sau đây là đúng?

A. ${(\vec{a} + \vec{b})}^{2} = {\vec{a}}^{2} + {\vec{b}}^{2}$

B. ${(\vec{a} + \vec{b})}^{2} = {\vec{a}}^{2} - 2 \vec{a} . \vec{b} + {\vec{b}}^{2}$

C. ${(\vec{a} + \vec{b})}^{2} = {\vec{a}}^{2} + 2 \vec{a} . \vec{b} + {\vec{b}}^{2}$

D. ${(\vec{a} + \vec{b})}^{2} = - {\vec{a}}^{2} + 2 \vec{a} . \vec{b} - {\vec{b}}^{2}$

Xem đáp án

${(\vec{a} + \vec{b})}^{2} = {\vec{a}}^{2} + 2 \vec{a} . \vec{b} + {\vec{b}}^{2}$

CHỌN C

Câu 19:

17/06/2026

Cho các vectơ $\vec{a}, \vec{b} k h á c \vec{0}$ . Khẳng định nào sau đây là đúng?

A. $\vec{a} ⊥ \vec{b} \Leftrightarrow \vec{a} . \vec{b} = |\vec{a}| . |\vec{b}|$

B. $\vec{a} ⊥ \vec{b} \Leftrightarrow \vec{a} . \vec{b} = 0$

C. $\vec{a} ⊥ \vec{b} \Leftrightarrow |\vec{a}| = |\vec{b}|$

D. $a ⃗ ⊥ b ⃗ ⟺ a ⃗^{2} = b ⃗^{2}$

Xem đáp án

Ta có: $\vec{a} ⊥ \vec{b} \Leftrightarrow (\vec{a}; \vec{b}) = 90^{0} \Leftrightarrow \vec{a} . \vec{b} = |\vec{a}| . |\vec{b}| . c os (\vec{a}; \vec{b}) = 0$

Chọn B.

Câu 20:

17/06/2026

Cho các vectơ $\vec{a}, \vec{b} k h á c \vec{0}$ . Nếu $\vec{a}, \vec{b}$ cùng hướng thì

A. $\vec{a} . \vec{b} = |\vec{a}| . |\vec{b}|$

B. $\vec{a} . \vec{b} = - |\vec{a}| . |\vec{b}|$

C. $\vec{a} . \vec{b} < |\vec{a}| . |\vec{b}|$

D. $\vec{a} . \vec{b} = 0$

Xem đáp án

Nếu 2 vecto $\vec{a}; \vec{b}$ cùng hướng thì $(\vec{a}; \vec{b}) = 0^{0} \Rightarrow \vec{a} . \vec{b} = |\vec{a}| . |\vec{b}| . c os (\vec{a}; \vec{b}) = |\vec{a}| . |\vec{b}|$

Chọn A.

Câu 21:

17/06/2026

Cho các vectơ $\vec{a}, \vec{b} k h á c \vec{0}$ . Nếu $\vec{a}, \vec{b}$ ngược hướng thì

A. $\vec{a} . \vec{b} = |\vec{a}| . |\vec{b}|$

B. $\vec{a} . \vec{b} = - |\vec{a}| . |\vec{b}|$

C. $\vec{a} . \vec{b} < |\vec{a}| . |\vec{b}|$

D. $\vec{a} . \vec{b} = 0$

Xem đáp án

Nếu 2 vecto $\vec{a}; \vec{b}$ ngược hướng thì $(\vec{a}; \vec{b}) = 180^{0} \Rightarrow \vec{a} . \vec{b} = |\vec{a}| . |\vec{b}| . c os (\vec{a}; \vec{b}) = - |\vec{a}| . |\vec{b}|$

Chọn B.

Câu 22:

17/06/2026

Khẳng định nào sau đây đúng?

A. $\exists \vec{a}, {|\vec{a}|}^{2} = |{\vec{a}}^{2}|$

B. $\forall \vec{a}, {|\vec{a}|}^{2} = |{\vec{a}}^{2}|$

C. $\forall \vec{a}, {|\vec{a}|}^{2} < 0$

D. $\forall \vec{a}, {|\vec{a}|}^{2} > 0$

Xem đáp án

Với $\forall \vec{a} : {|\vec{a}|}^{2} = {\vec{a}}^{2} = |{\vec{a}}^{2}|$ (vì ${\vec{a}}^{2} \geq 0)$

Chọn B.

Câu 23:

17/06/2026

Cho các vectơ $\vec{a}, \vec{b} k h á c \vec{0}$ . Khẳng định nào sau đây đúng?

A. $\vec{a}, \vec{b}$ cùng phương khi và chỉ khi $\vec{a} . \vec{b} = |\vec{a}| . |\vec{b}|$

B. $\vec{a}, \vec{b}$ cùng phương khi và chỉ khi $\vec{a} . \vec{b} = - |\vec{a}| . |\vec{b}|$

C. $\vec{a}, \vec{b}$ cùng phương khi và chỉ khi $\vec{a} . \vec{b} \neq |\vec{a}| . |\vec{b}|$

D. $\vec{a}, \vec{b}$ cùng phương khi và chỉ khi $|\vec{a} . \vec{b}| = |\vec{a}| . |\vec{b}|$

Xem đáp án

Nếu 2 vecto $\vec{a}; \vec{b}$ cùng phương thì $(\vec{a}; \vec{b}) = 180^{0}$ hoặc $(\vec{a}; \vec{b}) = 0^{0}$

$\Leftrightarrow c os (\vec{a}; \vec{b}) = - 1$ hoặc $c os (\vec{a}; \vec{b}) = 1$

$\Leftrightarrow |c os (\vec{a}; \vec{b})| = 1$

Ta có: $\vec{a} . \vec{b} = |\vec{a}| . |\vec{b}| . c os (\vec{a}; \vec{b})$

$\Rightarrow |\vec{a} . \vec{b}| = |\vec{a}| . |\vec{b}| . |c os (\vec{a}; \vec{b})| = |\vec{a}| . |\vec{b}| .1 = |\vec{a}| . |\vec{b}|$

Chọn D.

Câu 24:

17/06/2026

Cho các vectơ không cùng phương $\vec{a}, \vec{b}, \vec{c} k h á c \vec{0}$ . Khẳng định nào sau đây không đúng?

A. $(\vec{a} + \vec{b}) . \vec{c} = \vec{a} . \vec{c} + \vec{b} . \vec{c}$

B. $(\vec{a} . \vec{b}) . \vec{c} = \vec{a} . (\vec{b} . \vec{c})$

C. $(\vec{a} - \vec{b}) . \vec{c} = \vec{a} . \vec{c} - \vec{b} . \vec{c}$

D. $[(\vec{a} + \vec{b}) + \vec{c}] . [(\vec{a} + \vec{b}) - \vec{c}] = {\vec{a}}^{2} + 2 \vec{a} . \vec{b} + {\vec{b}}^{2} - {\vec{c}}^{2}$

Xem đáp án

Ta có: $(\vec{a} . \vec{b}) . \vec{c}$ là một vecto cùng phương với vecto $\vec{c}$ .

$\vec{a} . (\vec{b} . \vec{c}) $ là một vecto cùng phương với vecto $\vec{a}$ .

Vì hai vecto $\vec{a}; \vec{c}$ không cùng phương nên 2 vecto $(\vec{a} . \vec{b}) . \vec{c}$ và $\vec{a} . (\vec{b} . \vec{c}) $ không cùng phương nên không thể bằng nhau.

Chọn B.

Câu 25:

17/06/2026

Cho các vectơ $\vec{a}, \vec{b} k h á c \vec{0}$ . Khẳng định nào sau đây đúng?

A. $(\vec{a}, \vec{b}) = 90 ° \Leftrightarrow \vec{a} . \vec{b} = \vec{0}$

B. $(\vec{a}, \vec{b}) = 90 ° \Leftrightarrow \vec{a} . \vec{b} \neq 0$

C. $(\vec{a}, \vec{b}) = 90 ° \Leftrightarrow \vec{a} . \vec{b} \neq \vec{0}$

D. $(\vec{a}, \vec{b}) = 90 ° \Leftrightarrow \vec{a} . \vec{b} = 0$

Xem đáp án

Vì $\vec{a}; \vec{b} \neq \vec{0} \Rightarrow |\vec{a}| = |\vec{b}| \neq 0$

Do đó, $\vec{a} . \vec{b} = |\vec{a}| . |\vec{b}| . c os (\vec{a}; \vec{b}) = 0 \Leftrightarrow c os (\vec{a}; \vec{b}) = 0 \Leftrightarrow (\vec{a}; \vec{b}) = 90^{0}$

Chọn D

Câu 26:

17/06/2026

Cho các vectơ $\vec{a}, \vec{b} k h á c \vec{0}$ . Khẳng định nào sau đây đúng?

A. $(\vec{a}, \vec{b}) = 0 ° \Leftrightarrow \vec{a} . \vec{b} = 0$

B. $(\vec{a}, \vec{b}) = 0 ° \Leftrightarrow \vec{a} . \vec{b} = |\vec{a}| . |\vec{b}|$

C. $(\vec{a}, \vec{b}) = 0 ° \Leftrightarrow \vec{a} . \vec{b} = - |\vec{a}| . |\vec{b}|$

D. $(\vec{a}, \vec{b}) = 0 ° \Leftrightarrow \vec{a} . \vec{b} = \vec{0}$

Xem đáp án

Ta có: $(\vec{a}; \vec{b}) = 0^{0} \Leftrightarrow c os (\vec{a}; \vec{b}) = 1$

Khi đó, $\vec{a} . \vec{b} = |\vec{a}| . |\vec{b}| . c os (\vec{a}; \vec{b}) = |\vec{a}| . |\vec{b}|$

Chọn B

Câu 27:

17/06/2026

Cho các vectơ $\vec{a}, \vec{b} k h á c \vec{0}$ . Khẳng định nào sau đây đúng?

A. $(\vec{a}, \vec{b}) = 180 ° \Leftrightarrow \vec{a} . \vec{b} = 0$

B. $(\vec{a}, \vec{b}) = 180 ° \Leftrightarrow \vec{a} . \vec{b} = |\vec{a}| . |\vec{b}|$

C. $(\vec{a}, \vec{b}) = 180 ° \Leftrightarrow \vec{a} . \vec{b} = - |\vec{a}| . |\vec{b}|$

D. $(\vec{a}, \vec{b}) = 180 ° \Leftrightarrow \vec{a} . \vec{b} = \vec{0}$

Xem đáp án

Ta có: $(\vec{a}; \vec{b}) = 180^{0} \Leftrightarrow c os (\vec{a}; \vec{b}) = - 1$

Khi đó, $\vec{a} . \vec{b} = |\vec{a}| . |\vec{b}| . c os (\vec{a}; \vec{b}) = - |\vec{a}| . |\vec{b}|$

Chọn C.

Câu 28:

17/06/2026

Khẳng định nào sau đây đúng?

A. $\vec{a} . \vec{b} = 0 \Leftrightarrow [\begin{matrix} \vec{a} = \vec{0} \\ \vec{b} = \vec{0} \end{matrix}$

B. $\vec{a} . \vec{b} = 0 \Leftrightarrow [\begin{matrix} \vec{a} = 0 \\ \vec{b} = 0 \end{matrix}$

C. $\vec{a} . \vec{b} = 0 \Leftrightarrow [\begin{matrix} \vec{a} = \vec{0} \\ \vec{b} = \vec{0} \end{matrix}$

D. $\vec{a} . \vec{b} \Leftrightarrow [\begin{matrix} \vec{a} = \vec{0} \\ \vec{b} = \vec{0} \\ \vec{a} ⊥ \vec{b} \end{matrix}$

Xem đáp án

Ta có: $\vec{a} . \vec{b} = |\vec{a}| . |\vec{b}| . c os (\vec{a}; \vec{b})$

Để $\vec{a} . \vec{b} = 0 \Leftrightarrow [ \begin{matrix} |\vec{a}| = 0 \\ \begin{array}{l} |\vec{b}| = 0 \\ c os (\vec{a}; \vec{b}) = 0 \end{array} \end{matrix} \Leftrightarrow [ \begin{matrix} \vec{a} = \vec{0} \\ \begin{array}{l} \vec{b} = \vec{0} \\ \vec{a} ⊥ \vec{b} \end{array} \end{matrix}$

Chọn D

Câu 29:

17/06/2026

Cho đoạn thẳng AB và điểm M nằm giữa hai điểm A và B. khẳng định nào sau đây là đúng?

A. $\vec{A M} . \vec{A B} = - A M . A B$

B. $\vec{A M} . \vec{A B} = A M . A B$

C. $\vec{A M} . \vec{A B} < 0$

D. $\vec{A M} . \vec{A B} > A M . A B$

Xem đáp án

$\vec{A M} . \vec{A B} = A M . A B . \cos (\vec{A M}, \vec{A B})$

$= A M . A B . \cos 0 ° = A M . A B .1 = A M . A B$

ĐÁP ÁN B

Câu 30:

17/06/2026

Cho đoạn thẳng AB và điểm M nằm giữa hai điểm A và B. khẳng định nào sau đây là đúng?

A. $\vec{M A} . \vec{M B} > 0$

B. $\vec{M A} . \vec{M B} < - M A . M B$

C. $\vec{M A} . \vec{M B} = - M A . M B$

D. $\vec{M A} . \vec{M B} = M A . M B$

Xem đáp án

$\vec{M A} . \vec{M B} = M A . M B . \cos (\vec{M A}, \vec{M B})$

$= M A . M B . \cos 180 ° = M A . M B . (- 1) = - M A . M B$

Chọn C

Câu 31:

17/06/2026

Cho điểm M nằm trên đường tròn đường kính AB. Giá trị của ${\vec{M A}}^{2} + \vec{M A} . \vec{A B}$ bằng

A. $\vec{0}$

B.0

C. $A B^{2}$

D. $\frac{1}{2} A B^{2}$

Xem đáp án

Vì điểm M nằm trên đường tròn đường kính AB nên $\hat{A M B} = 90^{0}$ ( góc nội tiếp chắn nửa đường tròn).

$\Rightarrow (\vec{M A}; \vec{M B}) = \hat{A M B} = 90^{0}$

Ta có: ${\vec{M A}}^{2} + \vec{M A} . \vec{A B} = \vec{M A} . (\vec{M A} + \vec{A B}) = \vec{M A} . \vec{M B} = 0$

Chọn B

Câu 32:

17/06/2026

Cho tam giác ABC vuông tại B. biểu thức $\vec{A B} . \vec{A C}$ bằng

A. $\vec{0}$

B.0

C. $A B^{2}$

D. $B C^{2}$

Xem đáp án

Vì tam giác ABC vuông tại B nên $\hat{A B C} = 90^{0} \Rightarrow (\vec{A B}; \vec{B C}) = 90^{0}$

$\vec{A B} . \vec{A C} = \vec{A B} . (\vec{A B} + \vec{B C}) = {\vec{A B}}^{2} + \vec{A B} . \vec{B C} = {\vec{A B}}^{2} + 0 = A B^{2}$

Chọn C.

Câu 33:

17/06/2026

Cho tam giác ABC có trực tâm H.

Biểu thức $\vec{A H} . (\vec{H B} - \vec{H C}) + \vec{B H} . (\vec{H C} - \vec{H A}) + \vec{C H} . (\vec{H A} - \vec{H B})$ bằng

A. $\vec{0}$

B.0

C. $A B^{2} + B C^{2} + C A^{2}$

D. $\frac{1}{2} (A B^{2} + B C^{2} + C A^{2})$

Xem đáp án

Vì H là trực tâm tam giác ABC nên:

$\begin{array}{l} A H ⊥ C B; B H ⊥ A C; C H ⊥ B A \\ \Rightarrow \vec{A H} . \vec{C B} = 0; \vec{B H} . \vec{A C} = 0; \vec{C H} . \vec{B A} = 0 \end{array}$

Ta có

$\vec{A H} . (\vec{H B} - \vec{H C}) + \vec{B H} . (\vec{H C} - \vec{H A}) + \vec{C H} . (\vec{H A} - \vec{H B})$

$= \vec{A H} . \vec{C B} + \vec{B H} . \vec{A C} + \vec{C H} . \vec{B A} = 0$

CHỌN B

Câu 34:

17/06/2026

Cho tam giác ABC vuông cân tại A, AB = a. Giá trị của $\vec{A B} . \vec{B C}$ là

A. $a^{2}$

B. $- \frac{1}{2} a^{2}$

C. $- a^{2}$

D. $- \frac{\sqrt{3}}{2} a^{2}$

Xem đáp án

Vì tam giác ABC vuông tại A nên: $\vec{A B} . \vec{A C} = 0$

$\vec{A B} . \vec{B C} = \vec{A B} . (\vec{A C} - \vec{A B}) = \vec{A B} . \vec{A C} - {\vec{A B}}^{2} = 0 - {\vec{A B}}^{2} = - a^{2}$

Chọn C.

Câu 35:

17/06/2026

Cho tam giác ABC vuông cân tại A, AB = a. Giá trị của $\vec{A C} . \vec{B C}$ là

A. $- a^{2}$

B. $a^{2}$

C. $- \frac{1}{2} a^{2}$

D. $2 a^{2}$

Xem đáp án

Vì tam giác ABC vuông tại A nên: $\vec{A B} . \vec{A C} = 0$

$\vec{A C} . \vec{B C} = \vec{A C} . (\vec{A C} - \vec{A B}) = {\vec{A C}}^{2} - \vec{A C} . \vec{A B} = A C^{2} - 0 = a^{2}$

Chọn B.

Câu 36:

17/06/2026

Cho tam giác ABC đều cạnh a. Giá trị của $\vec{A B} . \vec{B C}$ là

A. $a^{2}$

B. $\frac{1}{2} a^{2}$

C. $- \frac{1}{2} a^{2}$

D. $\frac{\sqrt{3}}{2} a^{2}$

Xem đáp án

Xác định được góc $(\vec{A B}, \vec{B C})$ là góc ngoài của góc $\hat{B}$ nên $(\vec{A B}, \vec{B C}) = 120^{0} .$

Do đó $\vec{A B} . \vec{B C} = A B . B C . c o s (\vec{A B}, \vec{B C}) = a . a . c o s 120^{0} = - \frac{a^{2}}{2} .$

Chọn C.

Câu 37:

17/06/2026

Cho hình vuông ABCD cạnh a. Giá trị của $\vec{A B} . \vec{A C}$ là

A. $a^{2}$

B. $\frac{1}{2} a^{2}$

C.- $\frac{1}{2} a^{2}$

D. $- \frac{\sqrt{3}}{2} a^{2}$

Xem đáp án

Áp dụng định lí Pytago vào tam giác vuông ABC ta có:

$A C^{2} = A B^{2} + B C^{2} = a^{2} + a^{2} = 2 a^{2}$

$\Rightarrow A C = a \sqrt{2}$

Ta có $(\vec{A B}, \vec{A C}) = \hat{B A C} = 45^{0}$ nên $\vec{A B} . \vec{A C} = A B . A C . \cos 45^{0} = a . a \sqrt{2} . \frac{\sqrt{2}}{2} = a^{2} .$

Chọn A.

Câu 38:

17/06/2026

Cho tam giác ABC vuông tại A và có AC = b; AB = c. Tính $\vec{B A} . \vec{B C}$

A. $\vec{B A} . \vec{B C} = b^{2} .$

B. $\vec{B A} . \vec{B C} = c^{2} .$

C. $\vec{B A} . \vec{B C} = b^{2} + c^{2} .$

D. $\vec{B A} . \vec{B C} = b^{2} - c^{2} .$

Xem đáp án

Tam giác ABC vuông tại A suy ra $A B ⊥ A C$ $\Rightarrow \vec{A B} . \vec{A C} = 0.$

Ta có $\vec{B A} . \vec{B C} = \vec{B A} . (\vec{B A} + \vec{A C}) = {\vec{B A}}^{2} + \vec{B A} . \vec{A C} = A B^{2} = c^{2} .$

Chọn B.

Câu 39:

17/06/2026

Cho hình vuông ABCD cạnh a. Tính $P = \vec{A C} . (\vec{C D} + \vec{C A}) .$

A.-1

B. $3 a^{2}$

C. $- 3 a^{2}$

D. $2 a^{2}$

Xem đáp án

Đáp án đúng là: C

*Phương pháp giải:

- Nắm vững lý thuyết và tính chất của tích vô hướng hai vectơ: góc giữa hai vectơ, tính chất và ứng dụng tích vô hướng

*Lời giải:

Từ giả thiết suy ra $A C = \sqrt{A B^{2} + B C^{2}} = \sqrt{a^{2} + a^{2}} = a \sqrt{2} .$

Ta có

$P = \vec{A C} . (\vec{C D} + \vec{C A}) = \vec{A C} . \vec{C D} + \vec{A C} . \vec{C A} = - \vec{C A} . \vec{C D} - {\vec{A C}}^{2}$

$= - C A . C D \cos (\vec{C A}, \vec{C D}) - A C^{2} = - a \sqrt{2} . a . \cos 45^{0} - {(a \sqrt{2})}^{2} = - 3 a^{2} .$

*Một số lý thuyết và dạng bài tập về vectơ:

- Định nghĩa góc giữa hai vectơ: Cho hai vectơ $\vec{a}$ và $\vec{b}$ đều khác vectơ $\vec{0}$ . Từ điểm O bất kì vẽ $\vec{O A} = \vec{a}$ , $\vec{O B} = \vec{b}$ , khi đó góc $\hat{A O B}$ ( $0^{o} \leq \hat{A O B} \leq 180^{o}$ ) là góc giữa hai vectơ $\vec{a}$ và $\vec{b}$ . Kí hiệu: $(\vec{a}, \vec{b})$ .

- Định nghĩa tích vô hướng: Cho hai vectơ $\vec{a}$ và $\vec{b}$ ( $\vec{a}, \vec{b} \neq \vec{0}$ ), khi đó tích vô hướng của $\vec{a}$ và $\vec{b}$ kí hiệu là $\vec{a} . \vec{b}$ và xác định bởi công thức: $\vec{a} . \vec{b} = |\vec{a}| . |\vec{b}| . \cos (\vec{a}, \vec{b})$ .

Chú ý:

+) Khi ít nhất một trong hai vectơ $\vec{a}$ và $\vec{b}$ bằng vectơ $\vec{0}$ ta quy ước: $\vec{a} . \vec{b} = 0$ .

+) Với hai vectơ $\vec{a}$ và $\vec{b}$ (), ta có: $\vec{a} . \vec{b} = 0 \Leftrightarrow \vec{a} ⊥ \vec{b}$ .

+) Tích vô hướng $\vec{a} . \vec{a}$ được kí hiệu là ${\vec{a}}^{2}$ và ta có: ${\vec{a}}^{2} = {|\vec{a}|}^{2}$ .

- Ứng dụng của tích vô hướng:

+) Độ dài của vectơ $\vec{a} = (a_{1}; a_{2})$ được tính theo công thức: $|\vec{a}| = \sqrt{{a_{1}}^{2} + {a_{2}}^{2}}$

+) Góc giữa hai vectơ $\vec{a} = (a_{1}; a_{2})$ và $\vec{b} = (b_{1}; b_{2})$ ( $\vec{a}; \vec{b} \neq \vec{0}$ ):

$\cos (\vec{a}; \vec{b}) = \frac{\vec{a} . \vec{b}}{|\vec{a}| . |\vec{b}|} = \frac{a_{1} b_{1} + a_{2} b_{2}}{\sqrt{a_{1}^{2} + a_{2}^{2}} . \sqrt{b_{1}^{2} + b_{2}^{2}}}$

+) Khoảng cách giữa hai điểm $A (x_{A}; y_{A})$ và $B (x_{B}; y_{B})$ được tính theo công thức:

$A B = \sqrt{{(x_{B} - x_{A})}^{2} + {(y_{B} - y_{A})}^{2}}$

Xem thêm các bài viết liên quan hay, chi tiết

75 câu trắc nghiệm Vectơ nâng cao Toán 10

Trắc nghiệm Tích vô hướng của hai vecto có đáp án – Toán lớp 10

Chứng minh đẳng thức về tích vô hướng của vectơ hoặc về độ dài đoạn thẳng

Câu 40:

17/06/2026

Cho tam giác ABC vuông tại B, AB = 9. Giá trị của $\vec{A B} . \vec{A C}$ bằng

A.0

B.3

C.81

D.9

Xem đáp án

Ta có: tam giác ABC vuông tại B nên $\vec{A B} ⊥ \vec{B C} \Rightarrow \vec{A B} . \vec{B C} = 0$

$\vec{A B} . \vec{A C} = \vec{A B} . (\vec{A B} + \vec{B C}) = {\vec{A B}}^{2} + \vec{A B} . \vec{B C} = A B^{2} + 0 = 81$

Chọn C.

Câu 41:

17/06/2026

Trong mặt phẳng tọa độ Oxy, cho $\vec{a} = (2; 1), \vec{b} = (- 4; 7)$ . Giá trị của $\vec{a} . \vec{b}$ là

A.1

B.-1

C.-56

D.56

Xem đáp án

$\vec{a} (2; 1); \vec{b} (- 4; 7) \Rightarrow \vec{a} . \vec{b} = 2. (- 4) + 1.7 = - 1$

CHỌN B

Câu 42:

17/06/2026

Trong mặt phẳng tọa độ Oxy, cho $a ⃗ = (1; - 3), b ⃗ = (6; x)$ . Hai vectơ đó vuông góc với nhau khi và chỉ khi

A. x = - 2

B. x = 2

C.x = -3

D.x = 3

Xem đáp án

Ta có: $\vec{a} . \vec{b} = 1.6 - 3. x = 6 - 3 x$

Để hai vecto này vuông góc với nhau khi:

$\vec{a} . \vec{b} = 0 \Leftrightarrow 6 - 3. x = 0 \Leftrightarrow x = 2$

Chọn B.

Câu 43:

17/06/2026

Trong mặt phẳng tọa độ Oxy, cho $\vec{u} = (- 1; x), \vec{v} = (2; 4)$ . Hai vectơ này có độ dài bằng nhau khi và chỉ khi

A. $x = \sqrt{19}$

B. $x = - \sqrt{19}$

C. $x = \sqrt{21}$

D. $x \in \{- \sqrt{19}; \sqrt{19}\}$

Xem đáp án

Ta có: $|\vec{u}| = \sqrt{{(- 1)}^{2} + x^{2}} = \sqrt{1 + x^{2}}; |\vec{v}| = \sqrt{2^{2} + 4^{2}} = \sqrt{20}$

Để hai vecto này có độ dài bằng nhau khi và chỉ khi: $\sqrt{1 + x^{2}} = \sqrt{20}$

$\Leftrightarrow 1 + x^{2} = 20 \Leftrightarrow x^{2} = 19 \Leftrightarrow x = \pm \sqrt{19}$

Chọn D.

Câu 44:

17/06/2026

Cho tứ giác ABCD. Biểu thức $\vec{A B} . \vec{C D} + \vec{B C} . \vec{C D} + \vec{C A} . \vec{C D}$ bằng

A. $\vec{0}$

B. $C D^{2}$

C.0

D. $A B^{2} + A C^{2} + A D^{2}$

Xem đáp án

$\vec{A B} . \vec{C D} + \vec{B C} . \vec{C D} + \vec{C A} . \vec{C D} = (\vec{A B} + \vec{B C} + \vec{C A}) . \vec{C D} = \vec{0} . \vec{C D} = 0$

CHỌN C

Câu 45:

17/06/2026

Cho hình thoi ABCD. Giá trị của $(\vec{A B} + \vec{A D}) . (\vec{B A} + \vec{B C})$ là

A.1

B.0

C. $A B^{2} - B C^{2}$

D. $A B^{2} + B C^{2}$

Xem đáp án

Do ABCD là hình thoi nên $\vec{A C} ⊥ \vec{B D} \Rightarrow \vec{A C} . \vec{B D} = 0$ . Ta có:

$(\vec{A B} + \vec{A D}) (\vec{B A} + \vec{B C}) = \vec{A C} . \vec{B D} = 0$

Chọn B.

Câu 46:

17/06/2026

Nếu điểm M nằm trên đường trung trực của đoạn thẳng AB thì $(\vec{M A} + \vec{M B}) . (\vec{M A} - \vec{M B})$ bằng

A.1

B. $- A B^{2}$

C.0

D. $A B^{2}$

Xem đáp án

Vì điểm M nằm trên đường trung trực của AB nên AM = MB.

Ta có: $(\vec{M A} + \vec{M B}) (\vec{M A} - \vec{M B}) = {\vec{M A}}^{2} - {\vec{M B}}^{2} = M A^{2} - M B^{2} = 0$

CHỌN C

Câu 47:

17/06/2026

Cho vectơ $\vec{a}$ . Khẳng định nào sau đây là đúng?

A. $\vec{a} . \vec{0} = \vec{0}$

B. $\vec{a} . \vec{0} = |\vec{a}|$

C. $\vec{a} . \vec{0} = 0$

D. $\vec{a} . \vec{0} = - |\vec{a}|$

Xem đáp án

Ta có: $|\vec{0}| = 0$

Do đó, với mọi $\vec{a}$ ta có: $\vec{a} . \vec{0} = |\vec{a}| . |\vec{0}| . c os (\vec{a}; \vec{0}) = 0$

Chọn C.

Câu 48:

17/06/2026

Trong mặt phẳng tọa độ Oxy, cho ba điểm A(3; -1); B(2; 10); C(-4; 2). Tính tích vô hướng $\vec{A B} . \vec{A C}$ .

A. 40

B. – 40

C. 26

D. – 26

Xem đáp án

Ta có $\vec{A B} = (- 1; 11), \vec{A C} = (- 7; 3)$ .

Suy ra $\vec{A B} . \vec{A C} = (- 1) . (- 7) + 11.3 = 40.$

Chọn A.

Câu 49:

17/06/2026

Trong mặt phẳng tọa độ Oxy, cho hai vectơ $\vec{a} = 4 \vec{i} + 6 \vec{j}$ và $\vec{b} = 3 \vec{i} - 7 \vec{j} .$ Tính tích vô hướng $\vec{a} . \vec{b} .$

A. – 30

B. 3

C. 30

D. 43

Xem đáp án

Từ giả thiết suy ra $\vec{a} = (4; 6)$ và $\vec{b} = (3; - 7) .$

Suy ra $\vec{a} . \vec{b} = 4.3 + 6. (- 7) = - 30.$

Chọn A.

Câu 50:

17/06/2026

Trong mặt phẳng tọa độ Oxy, cho hai vectơ $\vec{a} = (- 3; 2)$ và $\vec{b} = (- 1; - 7) .$ Tìm tọa độ vectơ $\vec{c}$ biết $\vec{c} . \vec{a} = 9$ và $\vec{c} . \vec{b} = - 20.$

A. $\vec{c} = (- 1; - 3) .$

B. $\vec{c} = (- 1; 3) .$

C. $\vec{c} = (1; - 3) .$

D. $\vec{c} = (1; 3) .$

Xem đáp án

Gọi $\vec{c} = (x; y) .$

Ta có $\{\begin{cases} \vec{c} . \vec{a} = 9 \\ \vec{c} . \vec{b} = - 20 \end{cases} \Leftrightarrow \{\begin{cases} - 3 x + 2 y = 9 \\ - x - 7 y = - 20 \end{cases} \Leftrightarrow \{\begin{cases} x = - 1 \\ y = 3 \end{cases} \Rightarrow \vec{c} = (- 1; 3) .$

Chọn B

Câu 51:

17/06/2026

Trong mặt phẳng tọa độ Oxy, cho hai vectơ $\vec{a} = (- 1; 1)$ và $\vec{b} = (2; 0)$ . Tính cosin của góc giữa hai vectơ $\vec{a}$ và $\vec{b}$

A. $\cos (\vec{a}, \vec{b}) = \frac{1}{\sqrt{2}} .$

B. $\cos (\vec{a}, \vec{b}) = - \frac{\sqrt{2}}{2} .$

C. $\cos (\vec{a}, \vec{b}) = - \frac{1}{2 \sqrt{2}} .$

D. $\cos (\vec{a}, \vec{b}) = \frac{1}{2} .$

Xem đáp án

Ta có $\cos (\vec{a}, \vec{b}) = \frac{\vec{a} . \vec{b}}{|\vec{a}| . |\vec{b}|} = \frac{- 1.2 + 1.0}{\sqrt{{(- 1)}^{2} + 1^{2}} . \sqrt{2^{2} + 0^{2}}} = - \frac{\sqrt{2}}{2} .$

Chọn B.

Câu 52:

17/06/2026

Trong mặt phẳng tọa độ Oxy, cho hai vectơ $\vec{a} = (4; 3)$ và $\vec{b} = (1; 7)$ . Tính góc giữa hai vectơ $\vec{a}$ và $\vec{b}$

A.90⁰

B. 60⁰

C. 45⁰

D. 30⁰

Xem đáp án

Ta có $\cos (\vec{a}, \vec{b}) = \frac{\vec{a} . \vec{b}}{|\vec{a}| . |\vec{b}|} = \frac{4.1 + 3.7}{\sqrt{16 + 9} . \sqrt{1 + 49}} = \frac{\sqrt{2}}{2} \Rightarrow (\vec{a}, \vec{b}) = 45^{0} .$

Chọn C.

Câu 53:

17/06/2026

Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có A(6; 0); B(3;1) và C(-1; -1). Tính số đo góc B của tam giác đã cho.

A. 15⁰

B.60⁰

C. 120⁰

D. 135⁰.

Xem đáp án

Ta có $\vec{B A} = (3; - 1)$ và $\vec{B C} = (- 4; - 2)$ . Suy ra:

$\begin{array}{l} \cos (\vec{B A}, \vec{B C}) = \frac{\vec{B A} . \vec{B C}}{|\vec{B A}| . |\vec{B C}|} = \frac{3. (- 4) + (- 1) . (- 2)}{\sqrt{9 + 1} . \sqrt{16 + 4}} = - \frac{\sqrt{2}}{2} \\ \Rightarrow \hat{B} = (\vec{B A}, \vec{B C}) = 135^{O} . \end{array}$

Chọn D.

Câu 54:

17/06/2026

Trong mặt phẳng tọa độ Oxy, cho hai vectơ $\vec{u} = \frac{1}{2} \vec{i} - 5 \vec{j}$ và $\vec{v} = k \vec{i} - 4 \vec{j} .$ Tìm k để vectơ $\vec{u}$ vuông góc với $\vec{v}$

A. k = 20

B. k = -20

C. k = -40

D. k= 40

Xem đáp án

Từ giả thiết suy ra $\vec{u} = (\frac{1}{2}; - 5), \vec{v} = (k; - 4) .$

Để $\vec{u} ⊥ \vec{v} \Leftrightarrow \vec{u} . \vec{v} = 0 \Leftrightarrow \frac{1}{2} k + (- 5) (- 4) = 0 \Leftrightarrow k = - 40$ .

Chọn C.

Câu 55:

17/06/2026

Trong mặt phẳng tọa độ Oxy, cho hai vectơ $\vec{a} = (- 2; 3)$ và $\vec{b} = (4; 1)$ . Tìm vectơ $\vec{d}$ biết $\vec{a} . \vec{d} = 4$ và $\vec{b} . \vec{d} = - 2$ .

A. $\vec{d} = (\frac{5}{7}; \frac{6}{7}) .$

B. $\vec{d} = (- \frac{5}{7}; \frac{6}{7}) .$

C. $\vec{d} = (\frac{5}{7}; - \frac{6}{7}) .$

D. $\vec{d} = (- \frac{5}{7}; - \frac{6}{7}) .$

Xem đáp án

Gọi $\vec{d} = (x; y)$ .

Từ giả thiết, ta có hệ $\{\begin{matrix} - 2 x + 3 y = 4 \\ 4 x + y = - 2 \end{matrix} \Leftrightarrow \{\begin{cases} x = - \frac{5}{7} \\ y = \frac{6}{7} \end{cases} .$

Chọn B.

Câu 56:

17/06/2026

Trong mặt phẳng tọa độ Oxy, cho ba vectơ $\vec{u} = (4; 1), \vec{v} = (1; 4)$ và $\vec{a} = \vec{u} + m . \vec{v}$ với $m \in ℝ .$ Tìm m để $\vec{a}$ vuông góc với trục hoành.

A. m = 4

B. m = -4

C. m = -2

D. m = 2

Xem đáp án

Ta có $\vec{a} = \vec{u} + m . \vec{v} = (4 + m; 1 + 4 m) .$

Trục hoành có vectơ đơn vị là $\vec{i} = (1; 0) .$

Vectơ $\vec{a}$ vuông góc với trục hoành $\Leftrightarrow \vec{a} . \vec{i} = 0 \Leftrightarrow 4 + m = 0 \Leftrightarrow m = - 4.$

Chọn B.

Câu 57:

17/06/2026

Trong mặt phẳng tọa độ Oxy, cho hai vectơ $\vec{u} = (4; 1)$ và $\vec{v} = (1; 4) .$ Tìm m để vectơ $\vec{a} = m . \vec{u} + \vec{v}$ tạo với vectơ $\vec{b} = \vec{i} + \vec{j}$ một góc 45⁰.

A. m = 4

B.m = -1/2

C.m = -1/4

D.m = 1/2

Xem đáp án

Ta có $\{\begin{cases} \vec{a} = m . \vec{u} + \vec{v} = (4 m + 1; m + 4) \\ \vec{b} = \vec{i} + \vec{j} = (1; 1) \end{cases} .$

Yêu cầu bài toán $\Leftrightarrow \cos (\vec{a}, \vec{b}) = \cos 45^{0} = \frac{\sqrt{2}}{2}$

$\Leftrightarrow \frac{(4 m + 1) .1 + (m + 4) .1}{\sqrt{2} \sqrt{{(4 m + 1)}^{2} + {(m + 4)}^{2}}} = \frac{\sqrt{2}}{2} \Leftrightarrow \frac{5 (m + 1)}{\sqrt{2} \sqrt{17 m^{2} + 16 m + 17}} = \frac{\sqrt{2}}{2}$

$\begin{array}{l} \Leftrightarrow 5 (m + 1) = \sqrt{17 m^{2} + 16 m + 17} \\ \Leftrightarrow \{\begin{cases} m + 1 \geq 0 \\ 25 m^{2} + 50 m + 25 = 17 m^{2} + 16 m + 17 \end{cases} \Leftrightarrow m = - \frac{1}{4} . \end{array}$

Chọn C.

Câu 58:

17/06/2026

Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có A(1; 4); B(3; 2); C(5; 4). Tính chu vi P của tam giác đã cho.

A. $P = 4 + 2 \sqrt{2} .$

B. $P = 4 + 4 \sqrt{2} .$

C. $P = 8 + 8 \sqrt{2} .$

D. $P = 2 + 2 \sqrt{2} .$

Xem đáp án

Ta có $\{\begin{cases} \vec{A B} = (2; - 2) \\ \vec{B C} = (2; 2) \\ \vec{C A} = (- 4; 0) \end{cases} \Rightarrow \{\begin{cases} A B = \sqrt{2^{2} + {(- 2)}^{2}} = 2 \sqrt{2} \\ B C = \sqrt{2^{2} + 2^{2}} = 2 \sqrt{2} \\ C A = \sqrt{{(- 4)}^{2} + 0^{2}} = 4 \end{cases}$

Vậy chu vi P của tam giác ABC là P =AB + BC + CA $= 4 + 4 \sqrt{2}$

Chọn B.

Câu 59:

17/06/2026

Trong mặt phẳng tọa độ Oxy, cho bốn điểm A( 7; -3); B( 8; 4); C ( 1; 5) và D(0; -2). Khẳng định nào sau đây đúng?

A. $\vec{A C} ⊥ \vec{C B} .$

B. Tam giác ABC đều.

C. Tứ giác ABCD là hình vuông.

D. Tứ giác ABCD không nội tiếp đường tròn.

Xem đáp án

Ta có

$\begin{array}{l} \{\begin{cases} \vec{A B} = (1; 7) \Rightarrow A B = \sqrt{1^{2} + 7^{2}} = 5 \sqrt{2} \\ \vec{B C} = (- 7; 1) \Rightarrow B C = 5 \sqrt{2} \\ \vec{C D} = (- 1; - 7) \Rightarrow C D = 5 \sqrt{2} \\ \vec{D A} = (7; - 1) \Rightarrow D A = 5 \sqrt{2} \end{cases} \\ \Rightarrow A B = B C = C D = D A = 5 \sqrt{2} . \end{array}$

Lại có: $\vec{A B} . \vec{B C} = 1 (- 7) + 7.1 = 0$ nên $A B ⊥ B C$ .

Từ đó suy ra ABCD là hình vuông.

Chọn C.

Câu 60:

17/06/2026

Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có A(-1, 1); B (1; 3) và C(1; -1). Khẳng định nào sau đây là đúng ?

A. Tam giác ABC đều.

B. Tam giác ABC có ba góc đều nhọn.

C. Tam giác ABC cân tại B.

D. Tam giác ABC vuông cân tại A.

Xem đáp án

Ta có $\vec{A B} = (2; 2), \vec{B C} = (0; - 4)$ và $\vec{A C} = (2; - 2) .$

Suy ra $\{\begin{cases} A B = A C = 2 \sqrt{2} \\ A B^{2} + A C^{2} = B C^{2} \end{cases} .$

Vậy tam giác ABC vuông cân tại A.

Chọn D

Câu 61:

17/06/2026

Trong mặt phẳng tọa độ Oxy, cho hai điểm A(-2; 4) và B(8; 4). Tìm tọa độ điểm C thuộc trục hoành sao cho tam giác ABC vuông tại C.

A. C (6; 0)

B. C (0; 0); C( 6; 0).

C. C(0; 0)

D.C(-1; 0)

Xem đáp án

Ta có $C \in O x$ nên C(c; 0) và $\{\begin{cases} \vec{C A} = (- 2 - c; 4) \\ \vec{C B} = (8 - c; 4) \end{cases} .$

Tam giác ABC vuông tại C nên $\vec{C A} . \vec{C B} = 0 \Leftrightarrow (- 2 - c) . (8 - c) + 4.4 = 0$

$\Leftrightarrow c^{2} - 6 c = 0 \Leftrightarrow [\begin{array}{l} c = 6 \to C (6; 0) \\ c = 0 \to C (0; 0) \end{array} .$

Chọn B.

Câu 62:

17/06/2026

Trong mặt phẳng tọa độ Oxy, cho ba điểm A(-4; 0); B(-5; 0) và C(3; 0). Tìm điểm M thuộc trục hoành sao cho $\vec{M A} + \vec{M B} + \vec{M C} = \vec{0} .$

A. M (-2; 0)

B. M(2; 0)

C. M(- 4; 0)

D. M(- 5; 0)

Xem đáp án

Ta có $M \in O x$ nên M(x;O) và $\{\begin{cases} \vec{M A} = (- 4 - x; 0) \\ \vec{M B} = (- 5 - x; 0) \\ \vec{M C} = (3 - x; 0) \end{cases} \Rightarrow \vec{M A} + \vec{M B} + \vec{M C} = (- 6 - 3 x; 0) .$

Do $\vec{M A} + \vec{M B} + \vec{M C} = \vec{0}$ nên $- 6 - 3 x = 0 \Leftrightarrow x = - 2 \Rightarrow M (- 2; 0) .$

Chọn A.

Câu 63:

17/06/2026

Trong mặt phẳng tọa độ Oxy, cho hai điểm M(-2; 2) và N(1; 1).Tìm tọa độ điểm P thuộc trục hoành sao cho ba điểm M; N; P thẳng hàng.

A. P(0; 4)

B. P(0; -4)

C. P(-4; 0)

D.P( 4; 0)

Xem đáp án

Ta có $P \in O x$ nên P(x; 0) và $\{\begin{cases} \vec{M P} = (x + 2; - 2) \\ \vec{M N} = (3; - 1) \end{cases} .$

Do M, N, P thẳng hàng nên $\frac{x + 2}{3} = \frac{- 2}{- 1} \Leftrightarrow x = 4 \Rightarrow P (4; 0) .$

Chọn D.

Câu 64:

17/06/2026

Trong mặt phẳng tọa độ Oxy, tìm điểm M thuộc trục hoành để khoảng cách từ đó đến điểm N(- 1; 4) bằng $2 \sqrt{5} .$

A. M(1; 0)

B.M(1; 0); M(- 3; 0)

C.M( 3; 0)

D. M(1; 0); M(3; 0)

Xem đáp án

Ta có $M \in O x$ nên M(m, 0) và $\vec{M N} = (- 1 - m; 4) .$

Theo giả thiết: $M N = 2 \sqrt{5} \Leftrightarrow |\vec{M N}| = 2 \sqrt{5} \Leftrightarrow \sqrt{{(- 1 - m)}^{2} + 4^{2}} = 2 \sqrt{5}$

$\Leftrightarrow {(1 + m)}^{2} + 16 = 20 \Leftrightarrow m^{2} + 2 m - 3 = 0 \Leftrightarrow [\begin{array}{l} m = 1 \Rightarrow M (1; 0) \\ m = - 3 \Rightarrow M (- 3; 0) \end{array} .$

Chọn B.

Câu 65:

17/06/2026

Trong mặt phẳng tọa độ Oxy, cho hai điểm A(1; 3) và B(4; 2). Tìm tọa độ điểm C thuộc trục hoành sao cho C cách đều hai điểm A và B

A. $C (- \frac{5}{3}; 0) .$

B. $C (\frac{5}{3}; 0) .$

C. $C (- \frac{3}{5}; 0) .$

D. $C (\frac{3}{5}; 0) .$

Xem đáp án

Ta có $C \in O x$ nên C(x, 0) và $\{\begin{cases} \vec{A C} = (x - 1; - 3) \\ \vec{B C} = (x - 4; - 2) \end{cases} .$

Do $C A = C B \Leftrightarrow C A^{2} = C B^{2}$ .

$\begin{array}{l} \Leftrightarrow {(x - 1)}^{2} + {(- 3)}^{2} = {(x - 4)}^{2} + {(- 2)}^{2} \\ \Leftrightarrow x^{2} - 2 x + 1 + 9 = x^{2} - 8 x + 16 + 4 \\ \Leftrightarrow 6 x = 10 \Leftrightarrow x = \frac{5}{3} \Rightarrow C (\frac{5}{3}; 0) \end{array}$

Chọn B.

Câu 66:

17/06/2026

Trong mặt phẳng tọa độ Oxy, cho hai điểm A(2; 2); B( 5; -2). Tìm điểm M thuộc trục hoành sao cho $\hat{A M B} = 90^{0} ?$

A. M(0; 1)

B. M( 6; 0)

C. M(2; 0)

D. M(0; 6)

Xem đáp án

Ta có $M \in O x$ nên M(m; 0) và $\{\begin{cases} \vec{A M} = (m - 2; - 2) \\ \vec{B M} = (m - 5; 2) \end{cases} .$

Vì $\hat{A M B} = 90^{0}$ suy ra $\vec{A M} . \vec{B M} = 0$ nên $(m - 2) (m - 5) + (- 2) .2 = 0.$

$\Leftrightarrow m^{2} - 7 m + 6 = 0 \Leftrightarrow [\begin{array}{l} m = 1 \\ m = 6 \end{array} \Rightarrow [\begin{array}{l} M (1; 0) \\ M (6; 0) \end{array} .$

Chọn B.

Câu 67:

17/06/2026

Trong mặt phẳng tọa độ Oxy cho hai điểm A( 1; -1) và B(3; 2).Tìm M thuộc trục tung sao cho $M A^{2} + M B^{2}$ nhỏ nhất.

A. M(0; 1)

B. M (0; -1)

C. $M (0; \frac{1}{2}) .$

D. $M (0; - \frac{1}{2}) .$

Xem đáp án

Ta có $M \in O y$ nên M(0; m) và $\{\begin{cases} \vec{M A} = (1; - 1 - m) \\ \vec{M B} = (3; 2 - m) \end{cases} .$

Khi đó $M A^{2} + M B^{2} = {|\vec{M A}|}^{2} + {|\vec{M B}|}^{2} = 1^{2} + {(- 1 - m)}^{2} + 3^{2} + {(2 - m)}^{2} = 2 m^{2} - 2 m + 15.$

$= 2 {(m - \frac{1}{2})}^{2} + \frac{29}{2} \geq \frac{29}{2}; \forall m \in ℝ .$

Suy ra ${\{M A^{2} + M B^{2}\}}_{\min} = \frac{29}{2} .$

Dấu $=$ xảy ra khi và chỉ khi $m = \frac{1}{2} \Rightarrow M (0; \frac{1}{2}) .$

Chọn C.

Câu 68:

17/06/2026

Trong mặt phẳng tọa độ Oxy, cho hình bình hành ABCD biết A(-2; 0); B(2; 5); C( 6; 2).Tìm tọa độ điểm D?

A. D(2; -3)

B. D(2; 3)

C. D(-2; -3)

D. D(-2; 3)

Xem đáp án

Gọi D(x; y)

Ta có $\vec{A D} = (x + 2; y)$ và $\vec{B C} = (4; - 3)$ .

Vì ABCD là hình bình hành nên $\vec{A D} = \vec{B C}$

$\{\begin{cases} x + 2 = 4 \\ y = - 3 \end{cases} \Leftrightarrow \{\begin{cases} x = 2 \\ y = - 3 \end{cases} \Rightarrow D (2; - 3) .$

Chọn A.

Câu 69:

17/06/2026

Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có A(1; 3); B(-2; 4); C ( 5; 3). Tìm tọa độ trọng tâm G của tam giác đã cho.

A. $G (2; \frac{10}{3}) .$

B. $G (\frac{8}{3}; - \frac{10}{3}) .$

C. $G (2; 5) .$

D. $G (\frac{4}{3}; \frac{10}{3}) .$

Xem đáp án

Tọa độ trọng tâm $G (x_{G}; y_{G})$ là $\{\begin{cases} x_{G} = \frac{1 - 2 + 5}{3} = \frac{4}{3} \\ y_{G} = \frac{3 + 4 + 3}{3} = \frac{10}{3} \end{cases} .$

Chọn D.

Câu 70:

17/06/2026

Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có A(- 4;1); B(2; 4); C(2; -2). Tìm tọa độ tâm I của đường tròn ngoại tiếp tam giác đã cho.

A. $I (\frac{1}{4}; 1) .$

B. $I (- \frac{1}{4}; 1) .$

C. $I (1; \frac{1}{4}) .$

D. $I (1; - \frac{1}{4}) .$

Xem đáp án

Gọi I(x, y). Ta có $\{\begin{cases} \vec{A I} = (x + 4; y - 1) \\ \vec{B I} = (x - 2; y - 4) \\ \vec{C I} = (x - 2; y + 2) \end{cases} .$

Do I là tâm đường tròn ngoại tiếp tam giác ABC nên:

$I A = I B = I C \Leftrightarrow \{\begin{cases} I A^{2} = I B^{2} \\ I B^{2} = I C^{2} \end{cases}$

$\begin{array}{l} \Leftrightarrow \{\begin{cases} {(x + 4)}^{2} + {(y - 1)}^{2} = {(x - 2)}^{2} + {(y - 4)}^{2} \\ {(x - 2)}^{2} + {(y - 4)}^{2} = {(x - 2)}^{2} + {(y + 2)}^{2} \end{cases} \\ \Leftrightarrow \{\begin{cases} {(x + 4)}^{2} = {(x - 2)}^{2} + 9 \\ y = 1 \end{cases} \Leftrightarrow \{\begin{cases} x = - \frac{1}{4} \\ y = 1 \end{cases} \end{array}$ .

Chọn B.

Câu 71:

17/06/2026

Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có A(-3; 0); B(3; 0) và C(2; 6). Gọi H(a,b) là tọa độ trực tâm của tam giác đã cho. Tính a+ 6b

A. 5

B. 6

C. 7

D. 8

Xem đáp án

Ta có $\{\begin{cases} \vec{A H} = (a + 3; b); \vec{B C} = (- 1; 6) \\ \vec{B H} = (a - 3; b); \vec{A C} = (5; 6) \end{cases} .$

Từ giả thiết, ta có:

$\begin{array}{l} \{\begin{array}{l} \vec{A H} . \vec{B C} = 0 \\ \vec{B H} . \vec{A C} = 0 \end{array} \Leftrightarrow \{\begin{cases} (a + 3) . (- 1) + b .6 = 0 \\ (a - 3) .5 + b .6 = 0 \end{cases} \\ \Leftrightarrow \{\begin{cases} a = 2 \\ b = \frac{5}{6} \end{cases} \Rightarrow a + 6 b = 7. \end{array}$

Chọn C.

Câu 72:

17/06/2026

Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có A( 4; 3); B(2; 7) và C(- 3; -8). Tìm toạ độ chân đường cao A’ kẻ từ đỉnh A xuống cạnh BC?

A. A’ (1; -4)

B. A’ (-1; 4)

C. A’ (1; 4)

D.A’ (4; 1)

Xem đáp án

Đáp án đúng: C

* Lời giải:

Gọi A’ (x; y).

Ta có $\{\begin{cases} \vec{A A'} = (x - 4; y - 3) \\ \vec{B C} = (- 5; - 15) \\ \vec{B A'} = (x - 2; y - 7) \end{cases} .$

Từ giả thiết, ta có $\{\begin{cases} A A' ⊥ B C \\ B, A', C thang hang \end{cases} \Leftrightarrow \{\begin{cases} \vec{A A'} . \vec{B C} = 0 & (1) \\ \vec{B A'} = k \vec{B C} & (2) \end{cases} .$

$(1) \Leftrightarrow - 5 (x - 4) - 15 (y - 3) = 0 \Leftrightarrow x + 3 y = 13.$

$(2) \Leftrightarrow \frac{x - 2}{- 5} = \frac{y - 7}{- 15} \Leftrightarrow 3 x - y = - 1.$

Giải hệ $\{\begin{cases} x + 3 y = 13 \\ 3 x - y = - 1 \end{cases} \Leftrightarrow \{\begin{cases} x = 1 \\ y = 4 \end{cases} \Rightarrow A' (1; 4) .$

*Phương pháp giải:

- Nắm kỹ lý thuyết về vectơ và dạng bài tính tích vô hướng của hai vecto

*Một số dạng bài về tích của vectơ với một số

*Lý thuyết cần nắm:

- Tích của vectơ với một số: Cho số k $\neq$ 0 và vectơ $\vec{a} \neq \vec{0}$ . Tích của vectơ $\vec{a}$ với số k là một vectơ, kí hiệu là $k \vec{a}$ , cùng hướng với $\vec{a}$ nếu k > 0, ngược lại, ngược hướng với $\vec{a}$ nếu k < 0 và có độ dài bằng $|k| |\vec{a}|$ .

- Tính chất: Với hai vectơ $\vec{a}$ và $\vec{b}$ bất kì, với mọi số h và k, ta có:

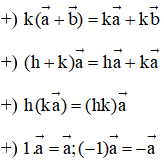
- Quy tắc trung điểm: Nếu I là trung điểm của đoạn thẳng AB thì với mọi điểm M ta có: $\vec{M A} + \vec{M B} = 2 \vec{M I}$

- Quy tắc trọng tâm: Nếu G là trọng tâm của tam giác ABC thì với mọi điểm M ta có: $\vec{M A} + \vec{M B} + \vec{M C} = 3 \vec{M G}$

Dạng 1: Tính độ dài vectơ khi biết tích vectơ với một số.

* Phương pháp giải: Sử dụng định nghĩa tích của vectơ với một số, các quy tắc về tổng, hiệu của các vectơ và các hệ thức lượng, định lý Py-ta-go để tính độ dài vectơ đó.

Dạng 2: Tìm một điểm thỏa mãn một đẳng thức vectơ cho trước.

* Phương pháp giải: Biến đổi đẳng thức đã cho về dạng $\vec{A M} = \vec{u}$ trong đó A là một điểm cố định, $\vec{u}$ cố định và dựng điểm M là điểm thỏa mãn $\vec{A M} = \vec{u}$ .

Xem thêm các bài viết liên quan hay, chi tiết

Chuyên đề Vectơ lớp 10 (có đáp án)

Trắc nghiệm Tổng hiệu của hai vecto có đáp án – Toán lớp 10

Trắc nghiệm Tích của vecto với một số có đáp án – Toán lớp 10

Câu 73:

17/06/2026

Trong mặt phẳng tọa độ Oxy, cho hai điểm A(2; 4) và B(1; 1). Tìm tọa độ điểm C sao cho tam giác ABC vuông cân tại B?

A. C(4; 0)

B.C(- 2; 2)

C. C(4; 0); C( -2; 2)

D. C(2; 0)

Xem đáp án

Gọi C(x, y).

Ta có $\{\begin{cases} \vec{B A} = (1; 3) \\ \vec{B C} = (x - 1; y - 1) \end{cases} .$

Tam giác ABC vuông cân tại B:

$\Leftrightarrow \{\begin{cases} \vec{B A} . \vec{B C} = 0 \\ B A = B C \end{cases}$ $\Leftrightarrow \{\begin{cases} 1. (x - 1) + 3. (y - 1) = 0 \\ 1^{2} + 3^{2} = {(x - 1)}^{2} + {(y - 1)}^{2} \end{cases}$

$\Leftrightarrow \{\begin{cases} x = 4 - 3 y \\ 10 y^{2} - 20 y = 0 \end{cases} \Leftrightarrow \{{\begin{matrix} y = 0 \\ x = 4 \end{matrix}}_{} {hay}_{} \{\begin{cases} y = 2 \\ x = - 2 \end{cases} .$

Chọn C.

Câu 74:

17/06/2026

Trong mặt phẳng tọa độ Oxy, cho hình vuông ABCD có A(1; -1) và B(3; 0). Tìm tọa độ điểm D, biết D có tung độ âm.

A.D(0; -1)

B. D( 2; -3)

C. D( 2; -3); D(0; 1)

D. D( -2; -3)

Xem đáp án

Gọi C= (x, y). Ta có $\{\begin{cases} \vec{A B} = (2; 1) \\ \vec{B C} = (x - 3; y) \end{cases} .$

Vì ABCD là hình vuông nên ta có $\{\begin{cases} \vec{A B} ⊥ \vec{B C} \\ A B = B C \end{cases}$

$\Leftrightarrow \{\begin{cases} 2 (x - 3) + 1. y = 0 \\ {(x - 3)}^{2} + y^{2} = 5 \end{cases} \Leftrightarrow \{\begin{array}{l} y = 2 (3 - x) \\ 5 {(x - 3)}^{2} = 5 \end{array} \Leftrightarrow \{\begin{cases} y = 2 (3 - x) \\ {(x - 3)}^{2} = 1 \end{cases} \Leftrightarrow \{\begin{cases} x = 4 \\ y = - 2 \end{cases}$ hoặc $\{\begin{matrix} x = 2 \\ y = 2 \end{matrix}$ .

Với $C_{1} (4; - 2)$ ta tính được đỉnh $D_{1} (2; - 3)$ : thỏa mãn.

Với $C_{2} (2; 2)$ ta tính được đỉnh $D_{2} (0; 1)$ : không thỏa mãn.

Chọn B.

Câu 75:

17/06/2026

Trong mặt phẳng tọa độ Oxy, cho tam giác OAB với A(1; 3) và B (4; 2). Tìm tọa độ điểm E là chân đường phân giác trong góc O của tam giác OAB

A. $E = (\frac{5}{2}; \frac{5}{2}) .$

B. $E = (\frac{3}{2}; - \frac{1}{2}) .$

C. $E = (- 2 + 3 \sqrt{2}; 4 + \sqrt{2}) .$

D. $E = (- 2 + 3 \sqrt{2}; 4 - \sqrt{2}) .$

Xem đáp án

Theo tính chất đường phân giác của tam giác ta có $\frac{E A}{E B} = \frac{O A}{O B} = \frac{\sqrt{2}}{2} .$

Vì E nằm giữa hai điểm A, B nên $\vec{E A} = - \frac{\sqrt{2}}{2} \vec{E B} .$ $(*)$

Gọi E(x; y). Ta có $\{\begin{cases} \vec{E A} = (1 - x; 3 - y) \\ \vec{E B} = (4 - x; 2 - y) \end{cases} .$

Từ (*), suy ra $\{\begin{cases} 1 - x = - \frac{\sqrt{2}}{2} (4 - x) \\ 3 - y = - \frac{\sqrt{2}}{2} (2 - y) \end{cases} \Leftrightarrow \{\begin{cases} x = - 2 + 3 \sqrt{2} \\ y = 4 - \sqrt{2} \end{cases} .$

Chọn D.

Lớp 1 - Cánh diều

Tiếng Anh 1

Toán lớp 1

Tiếng Việt lớp 1

Lớp 1 - Chân trời sáng tạo

Tiếng Anh 1

Toán lớp 1

Tiếng Việt lớp 1

Lớp 1 - Kết nối tri thức

Tiếng Anh 1

Toán lớp 1

Tiếng Việt lớp 1

Tiện ích

Đọc sách online

Bộ đề ôn hè lớp 1 lên lớp 2

Lớp 2 - Kết nối tri thức

Toán lớp 2

Tiếng Việt lớp 2

Đạo đức lớp 2

Tự nhiên và Xã hội lớp 2

Hoạt động trải nghiệm lớp 2

Tiếng Anh lớp 2

Âm nhạc lớp 2

Lớp 2 - Cánh diều

Toán lớp 2

Tiếng Việt lớp 2

Hoạt động trải nghiệm lớp 2

Tự nhiên và Xã hội lớp 2

Tiếng Anh lớp 2

Âm nhạc lớp 2

Đạo đức lớp 2

Lớp 2 - Chân trời sáng tạo

Toán lớp 2

Tiếng Việt lớp 2

Đạo đức lớp 2

Tự nhiên và Xã hội lớp 2

Hoạt động trải nghiệm lớp 2

Tiếng Anh lớp 2

Âm nhạc lớp 2

Tiện ích

Đọc sách online

Bộ đề ôn hè lớp 2 lên lớp 3

Lớp 3 - Kết nối tri thức

Toán lớp 3

Tiếng Anh lớp 3

Tiếng Việt lớp 3

Đạo đức lớp 3

Tự nhiên và Xã hội lớp 3

Hoạt động trải nghiệm lớp 3

Âm nhạc lớp 3

Tin học lớp 3

Giáo dục thể chất lớp 3

Công nghệ lớp 3

Lớp 3 - Cánh diều

Toán lớp 3

Tiếng Việt lớp 3

Tiếng Anh lớp 3

Đạo đức lớp 3

Tự nhiên và Xã hội lớp 3

Hoạt động trải nghiệm lớp 3

Âm nhạc lớp 3

Tin học lớp 3

Giáo dục thể chất lớp 3

Công nghệ lớp 3

Lớp 3 - Chân trời sáng tạo

Toán lớp 3

Tiếng Việt lớp 3

Tiếng Anh lớp 3

Đạo đức lớp 3

Tự nhiên và Xã hội lớp 3

Hoạt động trải nghiệm lớp 3

Âm nhạc lớp 3

Tin học lớp 3

Giáo dục thể chất lớp 3

Công nghệ lớp 3

Tiện ích

Đọc sách online

Bộ đề ôn hè lớp 3 lên lớp 4

Lớp 3 - Sách cũ

Tiếng Anh 3