15 câu hỏi trắc nghiệm thuộc Trắc nghiệm Các hệ thức lượng trong tam giác và giải tam giác có đáp án (Thông hiểu)

Câu 1:

20/07/2024

Tam giác ABC vuông tại A và có AB = AC = a. Tính độ dài đường trung tuyến BM của tam giác đã cho

A. $B M = 1, 5 a$

B. $B M = a \sqrt{2}$

C. $B M = a \sqrt{3}$

D. $B M = \frac{a \sqrt{5}}{2}$

Xem đáp án

Đáp án D

M là trung điểm của AC ⇒ AM = $\frac{A C}{2} = \frac{a}{2}$

Tam giác ΔBAM vuông tại A

$\Rightarrow B M = \sqrt{A B^{2} + A M^{2}} = \sqrt{a^{2} + \frac{a^{2}}{4}} = \frac{a \sqrt{5}}{2}$

Câu 2:

17/07/2024

Tam giác ABC có ba cạnh là 5, 12, 13. Khi đó, diện tích tam giác là:

A. 30

B. $20 \sqrt{2}$

C. $10 \sqrt{3}$

D. 20

Xem đáp án

Đáp án A

+ Ta có: $p = \frac{a + b + c}{2} = \frac{5 + 12 + 13}{2} = 15$

+ $S = \sqrt{p (p - a) (p - b) (p - c)}$

$= \sqrt{15.10.3.2} = \sqrt{900} = 30$

Câu 3:

14/07/2024

Tam giác ABC có a = 21, b = 17, c = 10. Diện tích của tam giác ABC bằng:

A. $S_{Δ A B C} = 16$

B. $S_{Δ A B C} = 48$

C. $S_{Δ A B C} = 24$

D. $S_{Δ A B C} = 84$

Xem đáp án

Đáp án D

+ Ta có: $p = \frac{21 + 17 + 10}{2} = 24$

+ $S = \sqrt{p (p - a) (p - b) (p - c)}$

$= \sqrt{24 (24 - 21) (24 - 17) (24 - 10)} = 84$

Câu 4:

22/07/2024

Tam giác ABC có đoạn thẳng nối trung điểm của AB và BC bằng 3, cạnh AB = 9 và $\hat{A C B} = 60^{0}$ . Tính độ dài cạnh BC

A. $B C = 3 + 3 \sqrt{6}$

B. $B C = 3 \sqrt{6} - 3$

C. $B C = 3 \sqrt{7}$

D. $B C = \frac{3 + 3 \sqrt{33}}{2}$

Xem đáp án

Đáp án A

Gọi M, N lần lượt là trung điểm của AB, BC.

⇒ MN là đường trung bình của ΔABC.

⇒ MN = $\frac{1}{2}$ AC. Mà MN = 3, suy ra AC = 6.

Theo định lí hàm cosin, ta có

$A B^{2} = A C^{2} + B C^{2} - 2 . A C . B C . \cos \hat{A C B} \Leftrightarrow 9^{2} = 6^{2} + B C^{2} - 2.6 . B C . \cos 60^{\circ} \Rightarrow B C = 3 + 3 \sqrt{6}$

Câu 5:

16/07/2024

Tam giác ABC có AB = 4, BC = 6, AC = $2 \sqrt{7}$ . Điểm M thuộc đoạn BC sao cho MC = 2MB. Tính độ dài cạnh AM?

A. $A M = 4 \sqrt{2}$

B. AM = 3

C. $A M = 2 \sqrt{3}$

D. $A M = 3 \sqrt{2}$

Xem đáp án

Đáp án C

Theo định lí hàm cosin, ta có:

$\cos B = \frac{A B^{2} + B C^{2} - A C^{2}}{2. A B . B C} = \frac{4^{2} + 6^{2} - {(2 \sqrt{7})}^{2}}{2.4.6} = \frac{1}{2}$

Do MC = 2MB $\Rightarrow B M = \frac{1}{3} B C = 2$

Theo định lí hàm cosin, ta có:

$A M^{2} = A B^{2} + B M^{2} - 2. A B . B M . \cos \hat{B} = 4^{2} + 2^{2} - 2.4.2. \frac{1}{2} = 12 \Rightarrow A M = 2 \sqrt{3}$

Câu 6:

19/07/2024

Tam giác ABC có BC = a, CA = b, AB = c và có diện tích S. Nếu tăng cạnh BC lên 2 lần đồng thời tăng cạnh CA lên 3 lần và giữ nguyên độ lớn của góc C thì khi đó diện tích tam giác mới được tạo nên bằng:

A. 2S

B. 3S

C. 4S

D. 6S

Xem đáp án

Đáp án D

+ Có $S = \frac{1}{2} B C . C A . \sin C$

+ Gọi S’ là diện tích tam giác khi tăng cạnh BC lên 2 lần đồng thời tăng cạnh CA lên 3 lần và giữ nguyên độ lớn của góc C, ta có:

$S' = \frac{1}{2} .2 B C .3 C A . \sin C = 6 S$

Câu 7:

18/10/2024

Tam giác ABC có BC = 10 và $\hat{A} = 30^{0}$ . Khi đó, bán kính đường tròn ngoại tiếp tam giác ABC là:

A. 5

B. 10

C. $\frac{10}{\sqrt{3}}$

D. $10 \sqrt{3}$

Xem đáp án

Đáp án đúng: B

*Phương pháp giải:

- Áp dụng định lý sin trong tam giác để tìm ra R

*Lời giải:

Từ $\frac{B C}{\sin A} = 2 R \Rightarrow R = \frac{B C}{2 \sin A} = \frac{10}{2 \sin 30^{0}} = 10$

* Các lý thuyết cần nắm về các công thức trong hệ thức lượng tam giác:

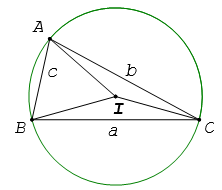
Định lí côsin

Cho tam giác ABC có BC = a, AC = b và AB = c. Ta có

a² = b² + c² – 2bc.cosA;

b² = c² + a² – 2ca.cosB;

c² = a² + b² – 2ab.cosC.

Hệ quả

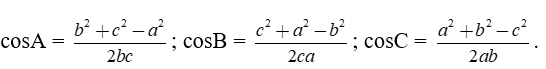
Định lí sin

Cho tam giác ABC có BC = a, AC = b, AB = c và R là bán kính đường tròn ngoại tiếp.

Ta có

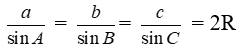
Toán lớp 10 | Chuyên đề: Lý thuyết và Bài tập Toán 10 có đáp án

Xem thêm các bài viết liên quan hay, chi tiết:

Lý thuyết Hệ thức lượng trong tam giác – Toán 10 Kết nối tri thức

Giải Toán 10 Bài 6 (Kết nối tri thức): Hệ thức lượng trong tam giác

Trắc nghiệm Các hệ thức lượng trong tam giác và giải tam giác (có đáp án)

Câu 8:

18/07/2024

Cho tam giác ABC có AB = 8cm, AC = 18cm và có diện tích bằng $64 c m^{2}$ . Giá trị $\sin \hat{A}$ là:

A. $\frac{\sqrt{3}}{2}$

B. $\frac{3}{8}$

C. $\frac{4}{5}$

D. $\frac{8}{9}$

Xem đáp án

Đáp án D

Ta có: $S = \frac{1}{2} A B . A C . \sin A$

$\Rightarrow \sin A = \frac{2 S}{A B . A C} = \frac{2.64}{8.18} = \frac{8}{9}$

Câu 9:

15/07/2024

Hình bình hành ABCD có AB = a, $B C = a \sqrt{2}$ và $\hat{B A D} = 45^{0}$ . Khi đó hình bình hành có diện tích bằng:

A. $2 a^{2}$

B. $a^{2} \sqrt{2}$

C. $a^{2}$

D. $a^{2} \sqrt{3}$

Xem đáp án

Đáp án C

Diện tích tam giác ABD là

$S_{Δ A B D} = \frac{1}{2} . A B . A D . \sin \hat{B A D}$

$= \frac{1}{2} . a . a \sqrt{2} . \sin 45^{0} = \frac{a^{2}}{2}$

Vậy diện tích hình bình hành ABCD là

$S_{Δ A B C D} = 2. S_{Δ A B D} = 2. \frac{a^{2}}{2} = a^{2}$

Câu 10:

06/12/2024

Tam giác ABC có AB = 5, BC = 7, CA = 8. Số đo góc $\hat{A}$ bằng:

A. $30^{\circ}$

B. $45^{\circ}$

C. $60^{\circ}$

D. $90^{\circ}$

Xem đáp án

Đáp án đúng là C

Lời giải

Theo định lí hàm cosin, ta có:

$\cos \hat{A} = \frac{A B^{2} + A C^{2} - B C^{2}}{2. A B . A C} = \frac{5^{2} + 8^{2} - 7^{2}}{2.5.8} = \frac{1}{2}$

Do đó, $\hat{A} = 60^{0}$

*Phương pháp giải:

Áp dụng hệ quả của định lí cosin

$\cos A = \frac{b^{2} + c^{2} - a^{2}}{2 b c};$

*Lý thuyết:

Định lí côsin trong tam giác

Định lí côsin: Trong tam giác ABC với BC = a, CA = b, AB = c, ta có:

a² = b² + c² – 2bc.cosA;

b² = c² + a² – 2ca.cosB;

c² = a² + b² – 2ab.cosC.

Từ định lí côsin, ta có hệ quả sau đây:

Hệ quả:

$\cos A = \frac{b^{2} + c^{2} - a^{2}}{2 b c};$

$\cos B = \frac{c^{2} + a^{2} - b^{2}}{2 c a};$

$\cos C = \frac{a^{2} + b^{2} - c^{2}}{2 a b} .$

xem thêm

Lý thuyết Định lí côsin và định lí sin – Toán 10 Chân trời sáng tạo

TOP 20 câu Trắc nghiệm Định lí côsin và định lí sin (Chân trời sáng tạo 2024) có đáp án - Toán 10

Câu 11:

14/07/2024

Tam giác ABC có ba cạnh là 6, 8, 10. Khi đó, bán kính đường tròn nội tiếp tam giác ABC là:

A. $\sqrt{3}$

B. 4

C. 2

D. 1

Xem đáp án

Đáp án C

+ Ta có: $p = \frac{6 + 8 + 10}{2} = 12$

+ $S = \sqrt{p (p - a) (p - b) (p - c)} = \sqrt{12.6.4.2} = 24$

+ $r = \frac{S}{p} = \frac{24}{12} = 2$

Câu 12:

17/07/2024

Tam giác ABC vuông tại A có AB = 6cm, BC = 10cm. Tính bán kính r của đường tròn nội tiếp tam giác đã cho

A. r = 1cm

B. $r = \sqrt{2} c m$

C. r = 2cm

D. r = 3cm

Xem đáp án

Đáp án C

Dùng Pytago tính được AC = 8, suy ra $p = \frac{A B + B C + C A}{2} = 12$

Diện tích tam giác vuông $S = \frac{1}{2} A B . A C = 24$

Lại có $S = p . r \Rightarrow r = \frac{S}{p} = 2 c m$

Câu 13:

13/11/2024

Tam giác ABC có AB = 5, AC = 8, và $\hat{B A C} = 60^{0}$ . Tính bán kính r của đường tròn nội tiếp tam giác đã cho

A. r = 1

B. r = 2

C. $r = \sqrt{3}$

D. $r = 2 \sqrt{3}$

Xem đáp án

Đáp án đúng là C

Lời giải:

Áp dụng định lí hàm số cosin, ta có:

$B C^{2} = A B^{2} + A C^{2} - 2 A B . A C . \cos A = 49 \Rightarrow B C = 7$

Diện tích $S = \frac{1}{2} A B . A C . \sin A = \frac{1}{2} .5.8. \frac{\sqrt{3}}{2} = 10 \sqrt{3}$

Lại có $S = p . r \Rightarrow r = \frac{S}{p} = \frac{2 S}{A B + B C + C A} = \sqrt{3}$

*Phương pháp giải:

Sử dụng định lí cosin

- Định lí Côsin:

Cho tam giác ABC bất kì với AB = c, AC = b, BC = a.

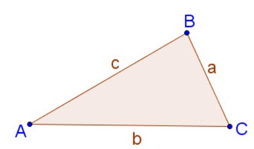
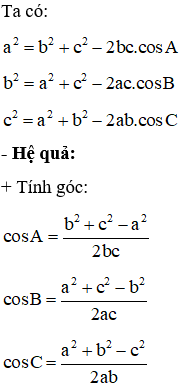
Công thức diẹn tích tam, giác

S = pr (với r là bán kính đường tròn nội tiếp,

*Lý thuyết:

- Định lí Côsin:

Cho tam giác ABC bất kì với AB = c, AC = b, BC = a.

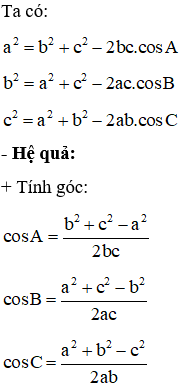
+ Tính diện tích:

$S = \frac{1}{2} B C . h_{a} = \frac{1}{2} A C . h_{b} = \frac{1}{2} A B . h_{c}$ . ( $h_{a}, h_{b}, h_{c}$ là độ dài đường cao lần lượt kẻ từ đỉnh A, B, C)

$S = \frac{1}{2} a b \sin C = \frac{1}{2} a c \sin B = \frac{1}{2} b c \sin A$

$S = \frac{a b c}{4 R}$ (với R là bán kính đường tròn ngoại tiếp)

S = pr (với r là bán kính đường tròn nội tiếp, $p = \frac{a + b + c}{2}$ )

$S = \sqrt{p (p - a) (p - b) (p - c)}$ (với $p = \frac{a + b + c}{2}$ ) (công thức Hê – rông)

Xem thêm

Tất tần tật về Định lí Côsin và hệ quả (2024) chi tiết nhất

TOP 40 câu Trắc nghiệm Tỉ số lượng giác của góc nhọn và Bảng lượng giác (có đáp án 2024) - Toán 9

Câu 14:

14/07/2024

Tam giác ABC có a = 21, b = 17, c = 10. Tính bán kính r của đường tròn nội tiếp tam giác đã cho

A. r = 16

B. r = 7

C. $r = \frac{7}{2}$

D. r = 8

Xem đáp án

Đáp án C

Ta có: $p = \frac{21 + 17 + 10}{2} = 24$

Suy ra $S = \sqrt{24 (24 - 21) (24 - 17) (24 - 10)} = 84$

Lạ có: $S = p . r \Rightarrow r = \frac{S}{p} = \frac{84}{24} = \frac{7}{2}$

Câu 15:

14/07/2024

Tính bán kính r của đường tròn nội tiếp tam giác đều cạnh a

A. $r = \frac{a \sqrt{3}}{4}$

B. $r = \frac{a \sqrt{2}}{5}$

C. $r = \frac{a \sqrt{3}}{6}$

D. $r = \frac{a \sqrt{5}}{7}$

Xem đáp án

Đáp án C

Diện tích tam giác đều cạnh a bằng:

$S = \frac{1}{2} a . a . \sin 60^{0} = \frac{a^{2} \sqrt{3}}{4}$

Lại có $S = p r \Rightarrow r = \frac{S}{p} = \frac{\frac{a^{2} \sqrt{3}}{4}}{\frac{3 a}{2}} = \frac{a \sqrt{3}}{6}$

Lớp 1 - Cánh diều

Tiếng Anh 1

Toán lớp 1

Tiếng Việt lớp 1

Lớp 1 - Chân trời sáng tạo

Tiếng Anh 1

Toán lớp 1

Tiếng Việt lớp 1

Lớp 1 - Kết nối tri thức

Tiếng Anh 1

Toán lớp 1

Tiếng Việt lớp 1

Tiện ích

Đọc sách online

Bộ đề ôn hè lớp 1 lên lớp 2

Giáo án lớp 1

Lớp 2 - Kết nối tri thức

Toán lớp 2

Tiếng Việt lớp 2

Đạo đức lớp 2

Tự nhiên và Xã hội lớp 2

Hoạt động trải nghiệm lớp 2

Tiếng Anh lớp 2

Âm nhạc lớp 2

Lớp 2 - Cánh diều

Toán lớp 2

Tiếng Việt lớp 2

Hoạt động trải nghiệm lớp 2

Tự nhiên và Xã hội lớp 2

Tiếng Anh lớp 2

Âm nhạc lớp 2

Đạo đức lớp 2

Lớp 2 - Chân trời sáng tạo

Toán lớp 2

Tiếng Việt lớp 2

Đạo đức lớp 2

Tự nhiên và Xã hội lớp 2

Hoạt động trải nghiệm lớp 2

Tiếng Anh lớp 2

Âm nhạc lớp 2

Đề thi các môn lớp 2

Đề thi các môn lớp 2 - Kết nối tri thức

Đề thi các môn lớp 2 - Cánh diều

Đề thi các môn lớp 2 - Chân trời sáng tạo

Tiện ích

Đọc sách online

Bộ đề ôn hè lớp 2 lên lớp 3

Giáo án lớp 2

Lớp 3 - Kết nối tri thức

Toán lớp 3

Tiếng Anh lớp 3

Tiếng Việt lớp 3

Đạo đức lớp 3

Tự nhiên và Xã hội lớp 3

Hoạt động trải nghiệm lớp 3

Âm nhạc lớp 3

Tin học lớp 3

Giáo dục thể chất lớp 3

Công nghệ lớp 3

Lớp 3 - Cánh diều

Toán lớp 3

Tiếng Việt lớp 3

Tiếng Anh lớp 3

Đạo đức lớp 3

Tự nhiên và Xã hội lớp 3

Hoạt động trải nghiệm lớp 3

Âm nhạc lớp 3

Tin học lớp 3

Giáo dục thể chất lớp 3

Công nghệ lớp 3

Lớp 3 - Chân trời sáng tạo

Toán lớp 3

Tiếng Việt lớp 3

Tiếng Anh lớp 3

Đạo đức lớp 3

Tự nhiên và Xã hội lớp 3

Hoạt động trải nghiệm lớp 3

Âm nhạc lớp 3

Tin học lớp 3

Giáo dục thể chất lớp 3