Câu hỏi:
13/11/2024 467Tam giác ABC có AB = 5, AC = 8, và ^BAC=600. Tính bán kính r của đường tròn nội tiếp tam giác đã cho
A. r = 1
B. r = 2
C. r=√3
D. r=2√3
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng là C
Lời giải:
Áp dụng định lí hàm số cosin, ta có:
BC2=AB2+AC2−2AB.AC.cosA=49⇒BC=7
Diện tích S=12AB.AC.sinA=12.5.8.√32=10√3
Lại có S=p.r⇒r=Sp=2SAB+BC+CA=√3
*Phương pháp giải:
Sử dụng định lí cosin
- Định lí Côsin:
Cho tam giác ABC bất kì với AB = c, AC = b, BC = a.
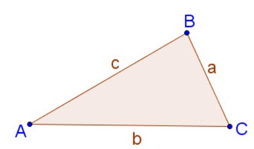
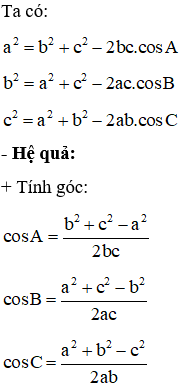
Công thức diẹn tích tam, giác
S = pr (với r là bán kính đường tròn nội tiếp,
*Lý thuyết:
- Định lí Côsin:
Cho tam giác ABC bất kì với AB = c, AC = b, BC = a.

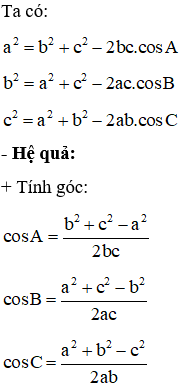
+ Tính diện tích:
S=12BC.ha=12AC.hb=12AB.hc. (ha,hb,hc là độ dài đường cao lần lượt kẻ từ đỉnh A, B, C)
S=12absinC=12acsinB=12bcsinA
S=abc4R (với R là bán kính đường tròn ngoại tiếp)
S = pr (với r là bán kính đường tròn nội tiếp, p=a+b+c2)
S=√p(p−a)(p−b)(p−c) (với p=a+b+c2) (công thức Hê – rông)
Xem thêm
Tất tần tật về Định lí Côsin và hệ quả (2024) chi tiết nhất
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 2:
Tam giác ABC có a = 21, b = 17, c = 10. Diện tích của tam giác ABC bằng:
Câu 3:
Tam giác ABC có a = 21, b = 17, c = 10. Tính bán kính r của đường tròn nội tiếp tam giác đã cho
Câu 4:
Tam giác ABC có BC = 10 và ˆA=300. Khi đó, bán kính đường tròn ngoại tiếp tam giác ABC là:
Câu 5:
Cho tam giác ABC có AB = 8cm, AC = 18cm và có diện tích bằng 64cm2. Giá trị sinˆA là:
Câu 6:
Tam giác ABC vuông tại A có AB = 6cm, BC = 10cm. Tính bán kính r của đường tròn nội tiếp tam giác đã cho
Câu 7:
Tam giác ABC có BC = a, CA = b, AB = c và có diện tích S. Nếu tăng cạnh BC lên 2 lần đồng thời tăng cạnh CA lên 3 lần và giữ nguyên độ lớn của góc C thì khi đó diện tích tam giác mới được tạo nên bằng:
Câu 8:
Tam giác ABC có ba cạnh là 5, 12, 13. Khi đó, diện tích tam giác là:
Câu 9:
Tam giác ABC có đoạn thẳng nối trung điểm của AB và BC bằng 3, cạnh AB = 9 và ^ACB=600. Tính độ dài cạnh BC
Câu 10:
Tam giác ABC có AB = 4, BC = 6, AC = 2√7. Điểm M thuộc đoạn BC sao cho MC = 2MB. Tính độ dài cạnh AM?
Câu 11:
Hình bình hành ABCD có AB = a, BC=a√2 và ^BAD=450. Khi đó hình bình hành có diện tích bằng:
Câu 12:
Tam giác ABC có ba cạnh là 6, 8, 10. Khi đó, bán kính đường tròn nội tiếp tam giác ABC là:
Câu 14:
Tam giác ABC vuông tại A và có AB = AC = a. Tính độ dài đường trung tuyến BM của tam giác đã cho


