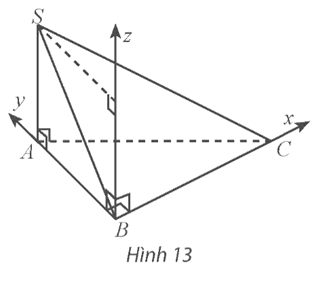
Cho tứ diện SABC có ABC là tam giác vuông tại B, BC = 3, BA = 2, SA vuông góc với mặt phẳng (ABC) và có độ dài bằng 2

Lời giải Bài 3 trang 56 Toán 12 Tập 1 sách Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 12.

1 8,821 16/06/2024

Trang trước

Trang sau

Giải Toán 12 Chân trời sáng tạo Bài 2: Toạ độ của vectơ trong không gian

Bài 3 trang 56 Toán 12 Tập 1: Cho tứ diện SABC có ABC là tam giác vuông tại B, BC = 3, BA = 2, SA vuông góc với mặt phẳng (ABC) và có độ dài bằng 2 (Hình 13).

a) Xác định một hệ tọa độ dựa trên gợi ý của hình vẽ và chỉ ra các vectơ đơn vị trên các trục tọa độ.

b) Tìm tọa độ các điểm A, B, C, S.

Bài 3 trang 56 Toán 12 Tập 1 Chân trời sáng tạo | Giải Toán 12

Lời giải:

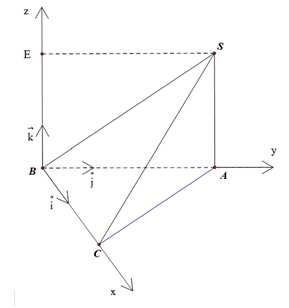
a)

Bài 3 trang 56 Toán 12 Tập 1 Chân trời sáng tạo | Giải Toán 12

Các vectơ đơn vị trên ba trục Ox, Oy, Oz lần lượt là $\vec{i}, \vec{j}, \vec{k}$ với độ dài của $\vec{i}, \vec{j}, \vec{k}$ lần lượt bằng $\frac{1}{3} B C, \frac{1}{2} B A, \frac{1}{2} S A$ .

b) Vì B trùng với gốc tọa độ nên B(0; 0; 0).

Vì $\vec{j}$ và $\vec{B A}$ cùng hướng và BA = 2 nên $\vec{B A} = 2 \vec{j}$ . Suy ra A(0; 2; 0).

Vì $\vec{i}$ và $\vec{B C}$ cùng hướng và BC = 3 nên $\vec{B C} = 3 \vec{i}$ . Suy ra C(3; 0; 0).

Gọi E là hình chiếu của S lên trục Oz.

Ta có BE = AS = 2.

Vì $\vec{k}$ và $\vec{B E}$ cùng hướng và BE = 2 nên $\vec{B E} = 2 \vec{k}$ .

Theo quy tắc hình bình hành ta có:

$\vec{B S} = \vec{B A} + \vec{B E} = 2 \vec{j} + 2 \vec{k}$ . Suy ra S(0; 2; 2).

Xem thêm các bài giải sách giáo khoa Toán 12 bộ sách Chân trời sáng tạo hay, chi tiết khác:

Hoạt động khởi động trang 52 Toán 12 Tập 1: Trong kiểm soát không lưu, người ta dùng bộ ba số để xác định vị trí của máy bay. Người ta đã làm điều đó như thế nào?

Hoạt động khám phá 1 trang 52 Toán 12 Tập 1: Cho hình lập phương OABC.O'A'B'C' có cạnh bằng 1. Đặt $\vec{i} = \vec{O A}, \vec{j} = \vec{O C}, \vec{k} = \vec{O O^{'}}$ ...

Thực hành 1 trang 53 Toán 12 Tập 1: Cho hình chóp S.ABCD có đáy là hình vuông cạnh bằng 1, SA vuông góc với mặt phẳng đáy và có độ dài bằng 1 (Hình 4)...

Vận dụng 1 trang 53 Toán 12 Tập 1: Một thiết kế cơ khí trong Hình 5a được biểu diễn trong không gian Oxyz như Hình 5b...

Hoạt động khám phá 2 trang 53 Toán 12 Tập 1: Cho hình hộp chữ nhật OABC.O'A'B'C' có cạnh OA = 3, OC = 5, OO' = 2. Vẽ ba vectơ đơn vị $\vec{i}, \vec{j}, \vec{k}$ lần lượt trên các cạnh OA, OC, OO'...

Thực hành 2 trang 54 Toán 12 Tập 1: Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng 5. Chọn hệ trục tọa độ Oxyz có gốc O trùng với A; các điểm B, D, A' lần lượt nằm trên các tia...

Hoạt động khám phá 3 trang 54 Toán 12 Tập 1: Trong không gian Oxyz, cho vectơ $\vec{a}$ . Vẽ điểm A sao cho $\vec{O A} = \vec{a}$ . Gọi $(a_{1}; a_{2}; a_{3})$ là tọa độ của điểm A...

Thực hành 3 trang 56 Toán 12 Tập 1: Cho hình chóp S.ABCD có đáy là hình vuông cạnh bằng 2, SA vuông góc với mặt phẳng đáy và có độ dài bằng 3 (Hình 11)...

Vận dụng 2 trang 56 Toán 12 Tập 1: Một máy bay đang cất cánh từ phi trường. Với hệ tọa độ Oxyz được thiết lập như Hình 12, cho biết M là vị trí của máy bay, OM = 14...

Bài 1 trang 56 Toán 12 Tập 1: Trong không gian Oxyz, biết: a) $\vec{a} = 5 \vec{i} + 7 \vec{j} - 3 \vec{k}, \vec{b} = 2 \vec{i} + 4 \vec{k}$ . Tìm tọa độ các vectơ $\vec{a}, \vec{b}$ ...

Bài 2 trang 56 Toán 12 Tập 1: Trong không gian Oxyz, biết: a) $\vec{a} = (- 2; 5; - 7)$ , $\vec{b} = (4; 0; 1)$ . Tính $\vec{a}, \vec{b}$ theo các vectơ $\vec{i}, \vec{j}, \vec{k}$ ...

Bài 3 trang 56 Toán 12 Tập 1: Cho tứ diện SABC có ABC là tam giác vuông tại B, BC = 3, BA = 2, SA vuông góc với mặt phẳng (ABC) và có độ dài bằng 2 (Hình 13)...

Bài 4 trang 57 Toán 12 Tập 1: Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh bằng 2, SA vuông góc với đáy và SA bằng 1 (Hình 14). Thiết lập hệ tọa độ như hình vẽ...

Bài 5 trang 57 Toán 12 Tập 1: Trong không gian Oxyz, cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh bằng 5, giao điểm hai đường chéo AC và BD trùng với gốc O...

Bài 6 trang 57 Toán 12 Tập 1: Một chiếc xe đang kéo căng sợi dây cáp AB trong công trường xây dựng, trên đó đã thiết lập hệ tọa độ Oxyz như Hình 16...

Bài 7 trang 57 Toán 12 Tập 1: Ở một sân bay, vị trí của máy bay được xác định bởi điểm M trong không gian Oxyz như Hình 17. Gọi H là hình chiếu vuông góc của M...

Xem thêm các bài giải sách giáo khoa Toán 12 bộ sách Chân trời sáng tạo hay, chi tiết khác:

Bài 1: Vectơ và các phép toán trong không gian

Bài 3: Biểu thức toạ độ của các phép toán vectơ

Bài tập cuối chương 2 trang 65

Bài 1: Khoảng biến thiên và khoảng tử phân vị của mẫu số liệu ghép nhóm

Bài 2: Phương sai và độ lệch chuẩn của mẫu số liệu ghép nhóm

1 8,821 16/06/2024

Trang trước

Trang sau

Xem thêm các chương trình khác: