28 câu hỏi trắc nghiệm thuộc Trắc nghiệm Tích của vecto với một số có đáp án (p1)

Câu 1:

13/07/2024

Cho vectơ $\vec{a}$ có $|\vec{a}| = 2$ . Tìm số thực x sao cho vectơ $x \vec{a}$ có độ dài bằng 1 và cùng hướng với $\vec{a}$

A. x = 1

B. x = 2

C. $x = \frac{1}{2}$

D. $x = - \frac{1}{2}$

Xem đáp án

Câu 2:

17/07/2024

Cho vectơ $\vec{a}, \vec{b}$ và các số thực m, n, k. Khẳng định nào sau đây là đúng?

A. Từ đẳng thức $m \vec{a} = n \vec{a}$ suy ra m = n

B. Từ đẳng thức $K \vec{a} = K \vec{b}$ luôn suy ra $\vec{a} = \vec{b}$

C. Từ đẳng thức $K \vec{a} = K \vec{b}$ luôn suy ra k = 0

D. Từ đẳng thức $m \vec{a} = n \vec{a}$ và $\vec{a} \neq 0$ suy ra m = n

Xem đáp án

Câu 3:

04/07/2024

Cho ba điểm A, B, C phân biệt sao cho $\vec{A B} = k \vec{A C}$ . Biết rằng B nằm giữa A và C. Giá trị k thỏa mãn điều kiện nào sau đây?

A. k < 0

B. k = 1

C. 0 < k < 1

D. k > 1

Xem đáp án

Vì B nằm giữa A và C nên $\vec{A B} = k \vec{A C}$ cùng hướng và AB < AC nên 0 < k < 1.

Chọn C.

Câu 4:

18/07/2024

Cho tam giác ABC với các trung tuyến AM, BN, CP. Khẳng định nào sau đây sai?

A. $\vec{A M} + \vec{B N} + \vec{C P} = \vec{0}$

B. $\vec{B M} + \vec{C N} + \vec{A P} = \vec{0}$

C. $\vec{C M} + \vec{A N} + \vec{B P} = \vec{0}$

D. $\vec{A M} + \vec{A N} + \vec{A P} = \vec{0}$

Xem đáp án

Ta có tứ giác ANMP là hình bình hành nên

Đáp án D

Câu 5:

17/07/2024

Cho tam giác ABC. Gọi M là điểm trên cạnh BC sao cho MB = 2MC. Khi đó khẳng định nào sau đây là đúng?

A. $\vec{A M} = \frac{1}{3} \vec{A B} + \frac{2}{3} \vec{A C}$

B. $\vec{A M} = \frac{2}{3} \vec{A B} + \frac{1}{3} \vec{A C}$

C. $\vec{A M} = \vec{A B} + \vec{A C}$

D. $\vec{A M} = \frac{2}{3} \vec{A B} - \frac{1}{3} \vec{A C}$

Xem đáp án

Câu 6:

22/07/2024

Các tam giác ABC và A’B’C’ có trọng tâm lần lượt là G và G’. Khẳng định nào sau đây là đúng?

A. $\vec{A A'} + \vec{B B'} + \vec{C C'} = \vec{G G'}$

B. $\vec{A A'} + \vec{B B'} + \vec{C C'} = \frac{1}{3} \vec{G G'}$

C. $\vec{A A'} + \vec{B B'} + \vec{C C'} = 3 \vec{G G'}$

D. $\vec{A A'} + \vec{B B'} + \vec{C C'} = \vec{0}$

Xem đáp án

Câu 7:

17/07/2024

Cho tứ giác ABCD; X là trọng tâm của tam giác BCD, G là trọng tâm tứ giác ABCD. Khẳng định nào sau đây đúng?

A. $\vec{G A} + \vec{G X} = \vec{0}$

B. $\vec{G A} + 3 \vec{G X} = \vec{0}$

C. $\vec{G B} + \vec{G X} = \vec{0}$

D. $\vec{G C} + \vec{G X} = \vec{0}$

Xem đáp án

Câu 8:

17/07/2024

Tam giác ABC có trọng tâm G, độ dài các cạnh BC, CA, AB lần lượt là a, b, c. Khi đó ABC là tam giác đều nếu có điều kiện nào sau đây?

A. $a \vec{G A} + b \vec{G B} + c \vec{G C} = \vec{0}$

B. $a \vec{G A} + b \vec{G B} - c \vec{G C} = \vec{0}$

C. $a \vec{G A} - b \vec{G B} + c \vec{G C} = \vec{0}$

D. $- a \vec{G A} + b \vec{G B} + c \vec{G C} = \vec{0}$

Xem đáp án

Đáp án A

Câu 9:

17/07/2024

Cho tam giác ABC và đường thẳng d. Vị trí của điểm M trên d sao cho $|\vec{M A} + \vec{M B} + \vec{M C}|$ có giá trị nhỏ nhất là:

A. Hình chiếu vuông góc của A trên d

B. Hình chiếu vuông góc của B trên d

C. Hình chiếu vuông góc của C trên d

D. Hình chiếu vuông góc của G trên d, với G là trọng tâm tam giác ABC

Xem đáp án

Chọn D.

Câu 10:

17/07/2024

Cho $\vec{a} = - 2 \vec{b}$ khẳng định nào sau đây là đúng?

A. $\vec{a} v à \vec{b}$ có giá trị trùng nhau

B. $\vec{a} v à \vec{b}$ cùng hướng

C. $\vec{a} v à \vec{b}$ ngược hướng và $|\vec{a}| = 2 |\vec{b}|$

D. $\vec{a} v à \vec{b}$ ngược hướng và $|\vec{a}| = - 2 |\vec{b}|$

Xem đáp án

Do $\vec{a} = - 2 \vec{b}$ nên hai vecto $\vec{a}; \vec{b}$ ngược hướng và $|\vec{a}| = |- 2| . |\vec{b}| = 2 . |\vec{b}|$

Đáp án C

Câu 11:

22/07/2024

Cho điểm B nằm giữa hai điểm A và C, AB = 2a, AC = 6a. khẳng định nào sau đây là đúng?

A. $\vec{B C} = 4 \vec{A C}$

B. $\vec{B C} = \vec{A B}$

C. $\vec{B C} = - 2 \vec{A B}$

D. $\vec{B C} = - 2 \vec{B A}$

Xem đáp án

Đáp án D

Câu 12:

17/07/2024

Cho vectơ $\vec{a}$ khác $\vec{0}$ . Phát biểu nào sau đây đúng?

A. Hai vectơ $\vec{a} v à - 2 \vec{a}$ cùng phương

B. Hai vectơ $\vec{a} v à - 2 \vec{a}$ cùng hướng

C. Hai vectơ $\vec{a} v à - 2 \vec{a}$ luôn có cùng gốc

D. Hai vectơ $\vec{a} v à - 2 \vec{a}$ luôn có giá song song với nhau

Xem đáp án

*Hai vectơ $\vec{a} v à - 2 \vec{a}$ cùng phương

* Hai vectơ $\vec{a} v à - 2 \vec{a}$ ngược hướng

* Hai vectơ $\vec{a} v à - 2 \vec{a}$ chưa chắc có cùng gốc

* Hai vectơ $\vec{a} v à - 2 \vec{a}$ có giá song song hoặc trùng nhau.

Đáp án A

Câu 13:

18/07/2024

Cho ba điểm A, B, C phân biệt. Điều kiện cần và đủ để ba điểm thẳng hàng là:

A. $\forall M : \vec{M A} + \vec{M B} + \vec{M C} = \vec{0}$

B. $\forall M : \vec{M A} + \vec{M C} = \vec{M B}$

C. $\vec{A C} = \vec{A B} + \vec{B C}$

D. $\exists k \in R : \vec{A B} = k \vec{A C}$

Xem đáp án

Với ba điểm A, B, C phân biệt. Điều kiện cần và đủ để ba điểm thẳng hàng là: $\exists k \in R : \vec{A B} = k \vec{A C}$

Đáp án D

Câu 14:

09/11/2024

Cho ba điểm A, B, C phân biệt. Điều kiện cần và đủ để ba điểm A, B, C thẳng hàng và A nằm giữa B, C là:

A. $\exists k < 0 : \vec{A B} = k \vec{A C}$

B. $\exists k \neq 0 : \vec{A B} = k \vec{A C}$

C. AB = AC

D. $\vec{A B} = \vec{A C}$

Xem đáp án

Đáp án đúng là A

LỜi giải

Với ba điểm A, B, C phân biệt.Khi A nằm giữa B, C thì hai vecto $\vec{A B}; \vec{A C}$ ngược hướng nên

điều kiện cần và đủ để ba điểm A, B, C thẳng hàng và A nằm giữa B, C là: $\exists k < 0 : \vec{A B} = k \vec{A C}$

*Phương pháp giải:

Ta sử dụng tính chất của 2 vectơ có cùng phương để có thể chứng minh có đường thẳng đi qua cả 3 điểm (tức là 3 điểm thẳng hàng)

Ví dụ: Chứng minh vectơ AB và vectơ AC có cùng phương, hay vectơ CA và vectơ CB, hay vectơ AB vectơ và vectơ BC có cùng phương thì ta có thể kết luận 3 điểm A, B, C thẳng hàng.

*Lý thuyết:

1. Định nghĩa

Ba điểm thẳng hàng là 3 điểm cùng nằm trên một đường thẳng

2. Mối quan hệ

3 điểm thẳng hàng thì 3 điểm đó phân biệt và cùng nằm trên một đường thẳng.

Chỉ có duy nhất 1 và chỉ một đường thẳng đi qua 3 điểm bất kì

3. Các phương pháp

Phương pháp 1: Áp dụng tính chất góc bẹt

Chọn một điểm D bất kì: nếu ∠ABD + ∠DBC = 180 độ thì ba điểm A, B, C đã cho thẳng hàng

Phương pháp 2: Sử dụng tiên đề Ơ-cơ-lit

Cho 3 điểm A, B, C và 1 đường thẳng a. Nếu AB // a và AC // a thì ta có thể khẳng định ba điểm A; B; C thẳng hàng. (dựa trên cơ sở tiên đề Ơ-cơ-lít trong chương trình Toán lớp 7)

Phương pháp 3: Sử dụng tính chất 2 đường thẳng vuông góc

Nếu đoạn thẳng AB ⊥ a; đoạn thẳng AC ⊥ a thì ba điểm A; B; C thẳng hàng.

(Cơ sở lý thuyết của phương pháp này: Chỉ có 1 và chỉ 1 một đường thẳng a’ đi qua điểm O và vuông góc với đường thẳng a cho trước)

Hoặc sử dụng tính chất A; B; C cùng thuộc một đường trung trực của một đoạn thẳng .(nằm trong chương trình toán học lớp 7)

Phương pháp 4: Sử dụng tính duy nhất tia phân giác

Nếu 2 tia OA và tia OB là hai tia phân giác của góc xOy thì ta có thể khẳng định 3 điểm O, A, B thẳng hàng

Cơ sở lý thuyết phương pháp trên: Một góc chỉ có một và chỉ một đường phân giác

* Hoặc : Hai tia OA và OB nằm trên cùng một nửa mặt phẳng bờ chứa tia Ox, ta có ∠xOA = ∠xOB thì ba điểm O, A, B thẳng hàng.

Phương pháp 5: Sử dụng tính chất đường trung trực

Nếu K là trung điểm của đoạn thẳng BD, điểm K’ là giao điểm của 2 đoạn thẳng BD và AC. Nếu điểm K’ là trung điểm BD và K’ trùng K. Từ đó ta có thể kết luận 3 điểm A, K, C thẳng hàng.

(Cơ sở lý thuyết của phương pháp này: Mỗi đoạn thẳng chỉ có duy nhất 1 trung điểm)

Phương pháp 6: Sử dụng tính chất các đường đồng quy

Chứng minh 3 điểm thuộc các đường đồng quy của tam giác.

Ví dụ: Chứng minh điểm E là trọng tâm tam giác ABC và đoạn thẳng AM là trung tuyến của góc A suy ra 3 điểm A, M, H thẳng hàng.

Bên cạnh đó, các em học sinh hoàn toàn có thể vận dụng cho tất cả các đường đồng quy khác của tam giác như 3 đường cao, 3 đường phân giác hoặc 3 đường trung trực trong tam giác.

Xem thêm

Các cách chứng minh 3 điểm thẳng hàng

80 câu trắc nghiệm Vectơ cơ bản (P1)

Câu 15:

18/07/2024

Cho hai vectơ $\vec{a}, \vec{b}$ khác $\vec{0}$ và cùng hướng. Khẳng định nào sau đây sai?

A. $\frac{\vec{a}}{|\vec{a}|} v à \frac{\vec{b}}{|\vec{b}|}$ cùng hướng

B. $\vec{b} = \frac{|\vec{b}|}{|\vec{a}|} \vec{a}$

C. $\vec{a} = \frac{|\vec{a}|}{|\vec{b}|} \vec{b}$

D. $\frac{\vec{a}}{|\vec{b}|} = \frac{\vec{b}}{|\vec{a}|}$

Xem đáp án

Câu 16:

21/07/2024

Nếu $\vec{A B} = - 3 \vec{A C}$ thì khẳng định nào sau đây là đúng?

A. $\vec{B C} = 4 \vec{A C}$

B. $\vec{B C} = - 4 \vec{A C}$

C. $\vec{B C} = 2 \vec{A C}$

D. $\vec{B C} = - 2 \vec{A C}$

Xem đáp án

Do $\vec{A B} = - 3 \vec{A C} \Rightarrow \vec{B A} = - 3 \vec{C A}$

ta có $\vec{B C} = \vec{B A} + \vec{A C} = - 3 \vec{C A} + \vec{A C} = 3 \vec{A C} + \vec{A C} = 4 \vec{A C}$

Đáp án A

Câu 17:

15/07/2024

Cho ba điểm phân biệt A, B, C sao cho $\vec{A B} = k \vec{A C}$ . Để A nằm giữa B và C thì k thỏa mãn điều kiện nào sau đây?

A. k = 1

B. k < 0

C. 0 < k < 1

D. k > 1

Xem đáp án

Để A nằm giữa B và C thì hai vecto $\vec{A B}; \vec{A C}$ ngược hướng nên k <0

Đáp án B

Câu 18:

19/07/2024

Trên đường thẳng BC lấy điểm M sao cho $\vec{M B} = - 3 \vec{M C}$ . Hình vẽ nào sau đây là đúng?

Xem đáp án

Để $\vec{M B} = - 3 \vec{M C}$ thì hai vecto $\vec{M B}; \vec{M C}$ ngược hướng nhau và MB = 3MC.

Khi đó, M nằm giữa B và C.

Đáp án D

Câu 19:

20/07/2024

Cho hai điểm M, N phân biệt. Điểm P thỏa mãn: $\vec{M N} = 4 \vec{P N}$ . Điểm P được xác định đúng trong hình vẽ nào sau đây?

Xem đáp án

Câu 20:

17/07/2024

Cho điểm K thuộc đoạn AB sao cho KA=2/3 KB. Khẳng định nào sau đây là sai?

A. $3 \vec{K A} + 2 \vec{K B} = \vec{0}$

B. $2 \vec{A B} = 5 \vec{A K}$

C. $\vec{K A} = - \frac{2}{5} \vec{A B}$

D. $\vec{K A} = \frac{2}{3} \vec{K B}$

Xem đáp án

Câu 21:

22/07/2024

Điều kiện nào dưới đây là điều kiện cần và đủ để điểm O là trung điểm của đoạn AB?

A. OA = OB

B. $\vec{O A} = \vec{O B}$

C. $\vec{A O} = \vec{B O}$

D. $\vec{O A} + \vec{O B} = \vec{0}$

Xem đáp án

Đáp án D

Câu 22:

18/07/2024

Cho hình bình hành ABCD tâm O. Đẳng thức nào sau đây đúng?

A. $\vec{A B} + \vec{A D} = 2 \vec{A C}$

B. $\vec{A B} + \vec{A D} + \vec{A C} = 2 \vec{A C}$

C. $\vec{A B} + \vec{A D} = \vec{A O}$

D. $\vec{A B} + \vec{A D} + \vec{A C} = 2 \vec{A O}$

Xem đáp án

Đáp án B

Câu 23:

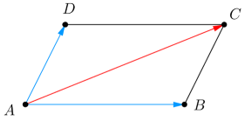
11/10/2024

Cho hình bình hành ABCD. Khẳng định nào sau đây đúng?

A. $\vec{A D} = \frac{1}{2} \vec{A C} - \frac{1}{2} \vec{B D}$

B. $\vec{C B} = \frac{1}{2} \vec{A C} - \frac{1}{2} \vec{B D}$

C. $\vec{D C} = \frac{1}{4} \vec{A C} - \frac{1}{2} \vec{B D}$

D. $\vec{A B} = \frac{1}{2} \vec{A C} - \frac{1}{2} \vec{B D}$

Xem đáp án

Đáp án đúng: D

* Phương pháp giải:

- Dùng định nghĩa tổng hiệu của hai vectơ, quy tắc ba điểm về tổng, quy tắc hình bình hành và các tính chất của tổng hiệu các vectơ.

* Lời giải:

$\begin{array}{l} \vec{A C} - \vec{B D} = \vec{A B} + \vec{B C} - \vec{B D} \\ = \vec{A B} + \vec{D C} = \vec{A B} + \vec{A B} = 2 \vec{A B} \\ \Rightarrow \vec{A B} = \frac{1}{2} \vec{A C} - \frac{1}{2} \vec{B D} \end{array}$

* Một số lý thuyết cần nhớ:

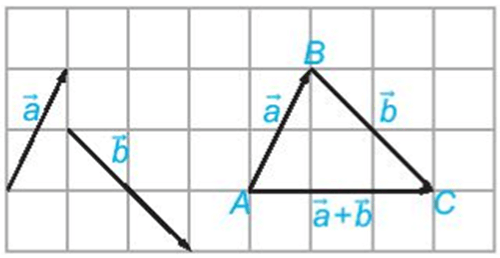
– Cho hai vectơ $\vec{a}$ và $\vec{b}$ . Lấy một điểm A tùy ý và vẽ $\vec{A B} = \vec{a}$ , $\vec{B C} = \vec{b}$ . Khi đó vectơ $\vec{A C}$ được gọi là tổng của hai vectơ $\vec{a}$ và $\vec{b}$ và được kí hiệu là $\vec{a}$ + $\vec{b}$ .

– Phép lấy tổng của hai vectơ được gọi là phép cộng vectơ.

– Quy tắc ba điểm: Với ba điểm bất kì A, B, C, ta có $\vec{A B} + \vec{B C} = \vec{A C}$ .

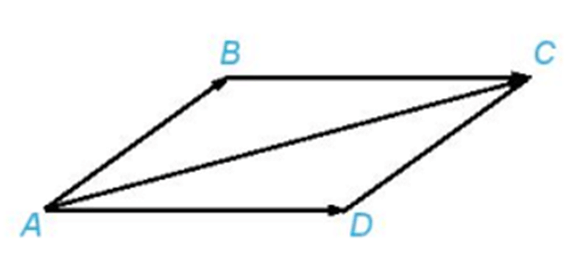
– Quy tắc hình bình hành: Nếu ABCD là hình bình hành thì $\vec{A B} + \vec{B C} = \vec{A C}$ .

– Với ba vectơ; $\vec{a}$ , $\vec{b}$ , $\vec{c}$ tùy ý :

+ Tính chất giao hoán: $\vec{a}$ + $\vec{b}$ = $\vec{b}$ + $\vec{a}$ ;

+ Tính chất kết hợp: ( $\vec{a}$ + $\vec{b}$ ) + $\vec{c}$ = $\vec{a}$ + ( $\vec{b}$ + $\vec{c}$ );

+ Tính chất của vectơ–không: $\vec{a}$ + $\vec{0}$ = $\vec{0}$ + $\vec{a}$ = $\vec{a}$ .

– Vectơ $\vec{a}$ + (– $\vec{b}$ ) được gọi là hiệu của hai vectơ $\vec{a}$ và $\vec{b}$ và được kí hiệu là $\vec{a}$ – $\vec{b}$ . Phép lấy hiệu hai vectơ được gọi là phép trừ vectơ.

– Nếu $\vec{b}$ + $\vec{c}$ = $\vec{a}$ thì $\vec{a}$ – $\vec{b}$ = $\vec{a}$ + (– $\vec{b}$ ) = $\vec{c}$ + $\vec{b}$ + (– $\vec{b}$ ) = $\vec{c}$ + $\vec{0}$ = $\vec{c}$ .

– Quy tắc hiệu: Với ba điểm O, M, N, ta có $\vec{M N} = \vec{M O} + \vec{O N} = (- \vec{O M}) + \vec{O N} = \vec{O N} - \vec{O M}$ .

Xem thêm các bài viết liên quan hay, chi tiết:

Trắc nghiệm Tổng và hiệu của hai vectơ có đáp án (Thông hiểu)

Trắc nghiệm Tổng và hiệu của hai vectơ có đáp án (Vận dụng)

Các dạng bài tập Vectơ

Câu 24:

10/07/2024

Cho tam giác ABC với trung tuyến AM và trọng tâm G. Khi đó $\vec{A G}$ bằng

A. $\frac{1}{2} \vec{G M}$

B. $- \frac{1}{3} \vec{A M}$

C. $\frac{2}{3} \vec{A M}$

D. $- \frac{2}{3} \vec{A M}$

Xem đáp án

Vì G là trọng tâm tam giác ABC nên: $\vec{A G} = \frac{2}{3} \vec{A M}$

Đáp án C

Câu 25:

11/11/2024

Cho tam giác ABC và điểm M thỏa mãn $\vec{M A} + \vec{M B} + 2 \vec{M C} = \vec{0}$ Khi đó điểm M là:

A. Trọng tâm tam giác ABC

B. Trung điểm của AB

C. Trung điểm của CC’ (C’ là trung điểm của AB)

D. Đỉnh thứ tư của hình bình hành ACBM

Xem đáp án

Đáp án đúng là C

Lời giải

*Phương pháp giải

Sử dụng quy tắc trung điểm

Quy tắc trung điểm: Với I là trung điểm của đoạn thẳng AB thì ta có:

$\vec{M A} + \vec{M B} = 2 \vec{M I}$ ( M tùy ý )

$\vec{I A} + \vec{I B} = \vec{0}$

*Lý thuyết

- Quy tắc trung điểm: Với I là trung điểm của đoạn thẳng AB thì ta có:

$\vec{M A} + \vec{M B} = 2 \vec{M I}$ ( M tùy ý )

$\vec{I A} + \vec{I B} = \vec{0}$

- Quy tắc trọng tâm: Với G là trọng tâm tam giác ABC thì ta có:

$\vec{M A} + \vec{M B} + \vec{M C} = 3 \vec{M G}$ ( M tùy ý )

$\vec{G A} + \vec{G B} + \vec{G C} = \vec{0}$

- Quy tắc hình bình hành: Nếu ABCD là hình bình hành thì $\vec{A B} + \vec{A D} = \vec{A C}$ .

Các công thức.

- Quy tắc trung điểm: I là trung điểm của AB

$\vec{I A} + \vec{I B} = \vec{0}$

$\vec{M A} + \vec{M B} = 2 \vec{M I}$ ( M tùy ý )

- Quy tắc trọng tâm: G là trọng tâm tam giác ABC

$\vec{M A} + \vec{M B} + \vec{M C} = 3 \vec{M G}$ ( M tùy ý )

$\vec{G A} + \vec{G B} + \vec{G C} = \vec{0}$

- Quy tắc hình hình hành: $\vec{A B} + \vec{A D} = \vec{A C}$ ( ABCD là hình bình hành )

Xem thêm

Quy tắc trung điểm, trọng tâm, quy tắc hình bình hành vecto (2024) chi tiết nhất

TOP 11 câu Trắc nghiệm Trung điểm của đoạn thẳng có lời giải - Toán lớp 6 Kết nối tri thức

Câu 26:

18/07/2024

Cho tam giác ABC có A’, B’, C’ lần lượt là trung điềm của các cạnh BC, CA, AB. Khẳng định nào sau đây là sai?

A. $\vec{B C'} = \vec{C' A} = \vec{A' B'}$

B. $\vec{B' C'} = \vec{A' B} = \vec{C A'}$

C. $\vec{C' A'} = \frac{1}{2} \vec{A C}$

D. $\vec{B A} + \vec{A B'} = \vec{A A'}$

Xem đáp án

Đáp án D

Câu 27:

13/07/2024

Cho tam giác ABC. Hỏi có bao nhiêu điểm M sao cho vectơ tổng $\vec{M A} + \vec{M B} + \vec{M C}$ có độ dài bằng 3?

A. Có duy nhất một điểm

B. Có hai điểm

C. Có vô số điểm và tập hợp các điểm M là một đường thẳng

D. Có vô số điểm và tập hợp các điểm M là một đường tròn

Xem đáp án

Đáp án D

Câu 28:

21/07/2024

Cho tam giác ABC có trọng tâm G, E là trung điểm của BC. Tập hợp các điểm M sao cho $2 |\vec{M A} + \vec{M B} + \vec{M C}| = 3 |\vec{M B} + \vec{M C}|$

A. Trung điểm của GE

B. Trung trực của GE

C. Trung trực của BC

D. Trọng tâm G

Xem đáp án

Suy ra tập họp các điểm M cần tìm là đường trung trực của đoạn GE.

Đáp án B

Lớp 1 - Cánh diều

Tiếng Anh 1

Toán lớp 1

Tiếng Việt lớp 1

Lớp 1 - Chân trời sáng tạo

Tiếng Anh 1

Toán lớp 1

Tiếng Việt lớp 1

Lớp 1 - Kết nối tri thức

Tiếng Anh 1

Toán lớp 1

Tiếng Việt lớp 1

Tiện ích

Đọc sách online

Bộ đề ôn hè lớp 1 lên lớp 2

Giáo án lớp 1

Lớp 2 - Kết nối tri thức

Toán lớp 2

Tiếng Việt lớp 2

Đạo đức lớp 2

Tự nhiên và Xã hội lớp 2

Hoạt động trải nghiệm lớp 2

Tiếng Anh lớp 2

Âm nhạc lớp 2

Lớp 2 - Cánh diều

Toán lớp 2

Tiếng Việt lớp 2

Hoạt động trải nghiệm lớp 2

Tự nhiên và Xã hội lớp 2

Tiếng Anh lớp 2

Âm nhạc lớp 2

Đạo đức lớp 2

Lớp 2 - Chân trời sáng tạo

Toán lớp 2

Tiếng Việt lớp 2

Đạo đức lớp 2

Tự nhiên và Xã hội lớp 2

Hoạt động trải nghiệm lớp 2

Tiếng Anh lớp 2

Âm nhạc lớp 2

Đề thi các môn lớp 2

Đề thi các môn lớp 2 - Kết nối tri thức

Đề thi các môn lớp 2 - Cánh diều

Đề thi các môn lớp 2 - Chân trời sáng tạo

Tiện ích

Đọc sách online

Bộ đề ôn hè lớp 2 lên lớp 3

Giáo án lớp 2

Lớp 3 - Kết nối tri thức

Toán lớp 3

Tiếng Anh lớp 3

Tiếng Việt lớp 3

Đạo đức lớp 3

Tự nhiên và Xã hội lớp 3

Hoạt động trải nghiệm lớp 3

Âm nhạc lớp 3

Tin học lớp 3

Giáo dục thể chất lớp 3

Công nghệ lớp 3

Lớp 3 - Cánh diều

Toán lớp 3

Tiếng Việt lớp 3

Tiếng Anh lớp 3

Đạo đức lớp 3

Tự nhiên và Xã hội lớp 3

Hoạt động trải nghiệm lớp 3

Âm nhạc lớp 3

Tin học lớp 3

Giáo dục thể chất lớp 3

Công nghệ lớp 3

Lớp 3 - Chân trời sáng tạo

Toán lớp 3

Tiếng Việt lớp 3

Tiếng Anh lớp 3

Đạo đức lớp 3

Tự nhiên và Xã hội lớp 3

Hoạt động trải nghiệm lớp 3

Âm nhạc lớp 3

Tin học lớp 3

Giáo dục thể chất lớp 3