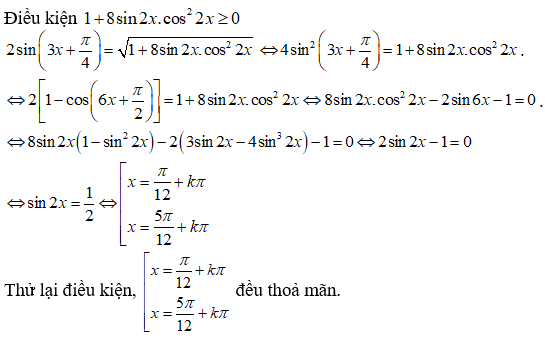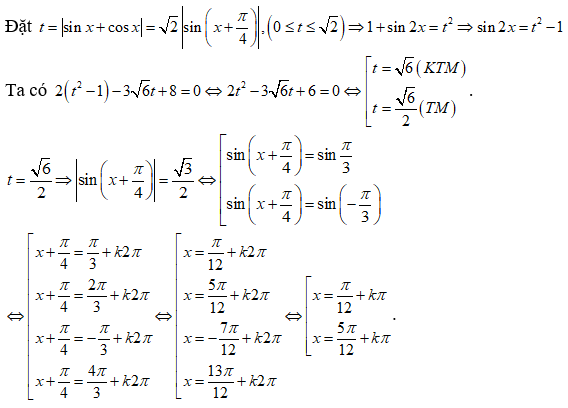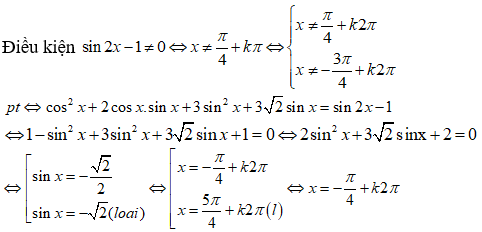20 câu hỏi trắc nghiệm thuộc 100 câu trắc nghiệm Phương trình lượng giác nâng cao (Đề số 3)

Câu 1:

17/07/2024

Số nghiệm thuộc [ $\frac{π}{14}$ ; $\frac{69 π}{10}$ ) của phương trình 2sin3x.(1 – 4sin²x) = 1 là:

A. 40

B. 32

C. 38

D. 46

Xem đáp án

Đáp án C

2sin3x(1 – 4.sin²x) = 1

$\Leftrightarrow 2 \sin 3 x (- 3 + 4 \cos^{2} x) = 1$ (1)

+) TH1: Nếu cosx = 0 thì sin²x = 1

$(1) \Leftrightarrow 2 \sin 3 x (- 3 + 4.0) = 1$

$\Leftrightarrow \sin 3 x = - \frac{1}{6}$

$\Leftrightarrow 3 \sin x - 4 \sin^{3} x = - \frac{1}{6}$

$\Leftrightarrow 3 \sin x - 4 s inx . \sin^{2} x = - \frac{1}{6}$

$\Leftrightarrow 3 \sin x - 4 \sin x = - \frac{1}{6}$

$\Leftrightarrow \sin x = \frac{1}{6}$ (vô lý)

+) TH2: Nếu cosx $\neq 0$ :

$(1) \Leftrightarrow 2 \sin 3 x (- 3 c os x + 4 \cos^{3} x) = c os x$

$\Leftrightarrow 2 \sin 3 x \cos 3 x = c osx$

$\Leftrightarrow \sin 6 x = c os x$

$\Leftrightarrow \sin 6 x = sin (\frac{π}{2} - x)$

$\Leftrightarrow [\begin{array}{l} 6 x = \frac{π}{2} - x + k 2 π \\ 6 x = π - \frac{π}{2} + x + k 2 π \end{array}, k \in ℤ$

$\Leftrightarrow [\begin{array}{l} x = \frac{π}{14} + k \frac{2 π}{7} \\ x = \frac{π}{10} + k \frac{2 π}{5} \end{array}, k \in ℤ$

Vì $x \in [\frac{π}{4}; \frac{69 π}{10})$

$\Rightarrow [\begin{array}{l} \frac{π}{4} \leq \frac{π}{14} + k \frac{2 π}{7} < \frac{69 π}{10} \\ \frac{π}{4} \leq \frac{π}{10} + h \frac{2 π}{5} < \frac{69 π}{10} \end{array}, k, h \in ℤ$

có 21 giá trị k và 17 giá trị h.

Vậy phương trình đã cho có tổng cộng có 21 + 17 = 38 nghiệm.

Câu 2:

17/07/2024

Các nghiệm thuộc khoảng (0; $\frac{π}{2}$ ) của phương trình sin³x.cos3x + cos³x.sin3x = $\frac{3}{8}$

A.

B.

C.

D.

Xem đáp án

Đáp án D

Câu 3:

18/07/2024

Phương trình $2 \sin (3 x + \frac{π}{4}) = \sqrt{1 + 8 \sin 2 x . \cos^{2} 2 x}$ có nghiệm là:

A.

B.

C.

D.

Xem đáp án

Đáp án B

Câu 4:

17/07/2024

Tìm số nghiệm x ∈ (0; π) của phương trình 5cosx + sinx - 3 = $\sqrt{2}$ sin(2x + $\frac{π}{4}$ ) (*)

A: 1

B: 2

C: 3

D: 4

Xem đáp án

Đáp án A

Câu 5:

20/07/2024

Tìm m để phương trình 2sin²x – (2m + 1)sinx + m = 0 có nghiệm x ∈ ( $\frac{- π}{2}$ ; 0).

A. -1 < m

B. 1 < m

C. -1 < m < 0

D. 0 < m < 1

Xem đáp án

Đáp án C

Câu 6:

17/07/2024

Phương trình $\sin^{3} x + \cos^{3} x + \sin^{3} x . cotx + \cos^{3} x . tanx = \sqrt{2 \sin 2 x}$ có nghiệm là:

A. x = $\frac{π}{8}$ + kπ

B. x = $\frac{π}{4}$ + kπ

C. x = $\frac{π}{4}$ + k2π

D. x = $\frac{3 π}{4}$ + k2π

Xem đáp án

Đáp án B

Kết hợp điều kiện, vậy nghiệm của phương trình đã cho là $x = \frac{π}{4} + k π$

Câu 7:

22/07/2024

Phương trình $\frac{\sin^{4} x + \cos^{4} x}{\sin 2 x} = \frac{1}{2} (tanx + cotx)$ có nghiệm là:

A. x = $\frac{π}{2}$ + kπ.

B. x = $\frac{π}{3}$ + k2π

C. x = $\frac{π}{4}$ + k $\frac{π}{2}$

D.Vô nghiệm

Xem đáp án

Đáp án D

Câu 8:

23/07/2024

Cho phương trình cos2x.cosx + sinx.cos3x = sin2x.sinx - sin3x.cosx và các họ số thực:

I. x = $\frac{π}{4}$ + kπ, k ∈ Z.

II. x = $\frac{- π}{2}$ + k2π, k ∈ Z.

III. x = $\frac{- π}{14}$ + $\frac{k 2 π}{7}$ , k ∈ Z.

IV. x = $\frac{π}{7}$ + $\frac{k 4 π}{7}$ , k ∈ Z.

Chọn trả lời đúng: Nghiệm của phương trình là:

A. I, II

B. I, III

C. II, III

D. II, IV.

Xem đáp án

Đáp án C

Câu 9:

17/07/2024

Tổng các nghiệm thuộc khoảng (0;2018) của phương trình $\sin^{4} \frac{x}{2} + \cos^{4} \frac{x}{2} = 1 - 2 \sin x$ là

A. 207046π

B. 206403π

C. 205761π

D. 204603π

Xem đáp án

Đáp án B

Câu 10:

17/07/2024

Tổng 2 nghiệm âm liên tiếp lớn nhất của phương trình 4sin³x – sinx – cosx = 0 bằng:

A.

B.

C.

D. -π

Xem đáp án

Đáp án B

+ Trường hợp 2. $\cos x \neq 0$ . chia cả hai vế cho $\cos^{3} x$ ta được:

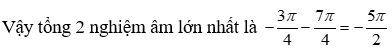
Câu 11:

22/07/2024

Cho phương trình sinx.cosx - sinx - cosx + m = 0, trong đó m là tham số thực. Để phương trình có nghiệm, các giá trị thích hợp của m là

A. $- 2 \leq m \leq - \frac{1}{2} - \sqrt{2}$

B. $- \frac{1}{2} - \sqrt{2} \leq m \leq 1$

C. $1 \leq m \leq \frac{1}{2} + \sqrt{2}$

D. $\frac{1}{2} + \sqrt{2} \leq m \leq 2$

Xem đáp án

Đáp án B

Câu 12:

17/07/2024

Phương trình 2sin2x - 3 $\sqrt{6}$ |sinx + cosx| + 8 = 0 có nghiệm là

A.

B.

C.

D.

Xem đáp án

Đáp án D

Câu 13:

23/07/2024

Tổng các nghiệm của phương trình sinx.cosx + |cosx + sinx| = 1 trên (0; 2π) là:

A. π

B. 2π

C. 3π

D. 4π

Xem đáp án

Đáp án C

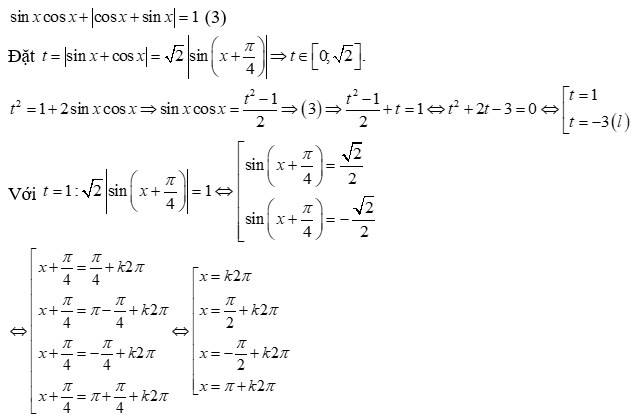
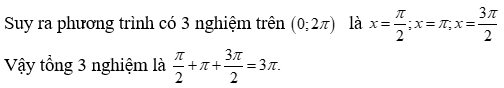
Câu 14:

23/07/2024

Có bao nhiêu giá trị nguyên của m để phương trình: sin2x + $\sqrt{2}$ sin(x - $\frac{π}{4}$ ) - m = 0 có nghiệm.

A.3

B.4

C.5

D.6

Xem đáp án

Đáp án B

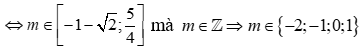
Câu 15:

08/12/2024

Giải phương trình $5 (sinx + \frac{\sin 3 x + \cos 3 x}{1 + 2 \sin 2 x}) = \cos 2 x + 3$

A. $x = \pm \frac{π}{3} + k 2 π, k \in ℤ$

B. x = ± $\frac{π}{6}$ + k2π, k ∈ $ℤ$

C. $x = \pm \frac{π}{3} + k π, k \in ℤ$

D. x = ± $\frac{π}{6}$ + kπ, k ∈ $ℤ$

Xem đáp án

Đáp án đúng là A

Lời giải

Điều kiện: $\sin 2 x \neq - \frac{1}{2} \Leftrightarrow \{\begin{cases} x \neq - \frac{π}{12} + k π \\ x = \frac{7 π}{12} + k π \end{cases}, k \in ℤ$

$5 (s inx + \frac{3 (s inx - c os x) - 4 (s inx - c os x) (1 + s inx . c os x)}{1 + 2 \sin 2 x}) = \cos 2 x + 3$

$\Leftrightarrow 5 (s inx + \frac{(s inx - c os x) (3 - 4 - 4 s inx . c os x)}{1 + 2 \sin 2 x}) = \cos 2 x + 3$

$\Leftrightarrow 5 (s inx + \frac{(s inx - c os x) (- 1 - 2 s in2x)}{1 + 2 \sin 2 x}) = \cos 2 x + 3$

$\Leftrightarrow 5 (s inx - s inx + c os x) = \cos 2 x + 3$

$\Leftrightarrow 5 c os x = 2 \cos^{2} x - 1 + 3$

$\Leftrightarrow 2 \cos^{2} x - 5 c os x + 2 = 0$

$\Leftrightarrow [\begin{array}{l} cos x = 2 (V L) \\ cosx= \frac{1}{2} \end{array} \Leftrightarrow cosx= \frac{1}{2} \Leftrightarrow x = \pm \frac{π}{3} + k 2 π, k \in ℤ$ (thỏa mãn điều kiện)

Vậy nghiệm của phương trình đã cho là: $x = \pm \frac{π}{3} + k 2 π, k \in ℤ$ .

*Phương pháp giải:

Sử dụng các công thức biến đổi lượng giác đã được học để đưa về phương trình bậc nhất đối với hàm số lượng giác hoặc đưa về phương trình tích để giải phương trình.

*Lý thuyết:

Định nghĩa:

Phương trình bậc hai đối với một hàm số lượng giác Là phương trình có dạng :

a.f²(x) + b.f(x) + c = 0

với f(x) = sinu(x) hoặc f(x) = cosu(x), tanu(x), cotu(x).

Cách giải:

Đặt t = f(x) ta có phương trình : at² + bt +c = 0

Giải phương trình này ta tìm được t, từ đó tìm được x

Khi đặt t = sinu(x) hoặc t = cosu(x), ta có điều kiện: -1 ≤ t ≤ 1

Xem thêm

Chuyên đề Một số phương trình lượng giác thường gặp (2024) và cách giải các dạng bài tập

50 Bài tập Phương trình lượng giác cơ bản Toán 11 mới nhất

Câu 16:

20/07/2024

Cho phương trình $\frac{1}{2} \cos 4 x + \frac{4 tanx}{1 + \tan^{2} x} = m$ . Để phương trình vô nghiệm, các giá trị của tham số m phải thỏa mãn điều kiện:

A. $- \frac{5}{2}$ ≤ m ≤ 0

B. m > 1

C. 0 < m

D. m $\leq$ $- \frac{5}{2}$ hay m > $\frac{3}{2}$ .

Xem đáp án

Đáp án D

Đặt t = sin 2x $; t \in [- 1; 1] \ {0}$

( 1) trở thành: $2 t^{2} - 4 t + 2 m - 1 = 0 (2) ∆' = 4 - 2 . (2 m - 1) = - 4 m + 6$

Ta tìm m để (2) có nghiệm $; t \in [- 1; 1] \ {0}$

+ Nếu $∆' = 0 \Leftrightarrow m = \frac{3}{2}$ thì (2) có nghiệm kép t = 1 ( thỏa mãn)

+ Nếu $∆' > 0 \Leftrightarrow m < \frac{3}{2}$ thì (2) có 2 nghiệm phân biệt.

Nếu (2) có nghiệm t = 0 thì m = 1/2. Và nghiệm còn lại là t = 2 $\notin [- 1; 1] \ {0}$

Do đó, (1) vô nghiệm khi $m \leq \frac{- 5}{2}$ hoặc $m > \frac{3}{2}$

Câu 17:

21/07/2024

Nghiệm phương trình: $\frac{cosx (cosx + 2 sinx) + 3 sinx (sinx + \sqrt{2})}{\sin 2 x - 1} = 1$

A. x = ± $\frac{π}{4}$ + k2π, k ∈ Z

B. x = $- \frac{π}{4}$ + kπ, k ∈ Z

C. x = $- \frac{π}{4}$ + k2π, x = $- \frac{3 π}{4}$ + k2π, k ∈ Z

D. x = $- \frac{π}{4}$ + k2π, k ∈ Z

Xem đáp án

Đáp án D

Câu 18:

01/12/2024

Cho phương trình cos5x.cosx = cos4x.cos2x + 3cos²x + 1. Các nghiệm thuộc khoảng (-π; π) của phương trình là:

A.

B.

C.

D.

Xem đáp án

Đáp án đúng là D

Lời giải

*Phương pháp giải:

Giải phương trình tìm nghiệm, kẹp nghiệm trong nửa khoảng đã cho tìm số nghiệm thỏa mãn.

*Lý thuyết:

- Định nghĩa phương trình bậc nhất một ẩn: Phương trình có dạng ax + b = 0, với a và b là hai số đã cho và a ≠ 0, được gọi là phương trình bậc nhất một ẩn.

Ví dụ 1.

4x – 3 = 2x là phương trình bậc nhất với ẩn x;

2(y – 1) + 8 = y + 3 là phương trình bậc nhất với ẩn y.

2. Hai quy tắc biến đổi phương trình

a) Quy tắc chuyển vế

Trong một phương trình, ta có thể chuyển một hạng tử từ vế này sang vế kia và đổi dấu hạng tử đó.

b) Quy tắc nhân với một số

Trong một phương trình, ta có thể nhân (chia) cả hai vế với cùng một số khác 0.

Xem thêm

Lý thuyết Phương trình bậc nhất một ẩn và cách giải (mới + Bài Tập) – Toán 8

TOP 40 câu Trắc nghiệm Phương trình bậc nhất một ẩn và cách giải (có đáp án ) - Toán 8

Câu 19:

17/07/2024

Giải phương trình 3tan²x + 4sin²x - 2 $\sqrt{3}$ tanx - 4sinx + 2 = 0

A. x = ± $\frac{π}{6}$ + k2π, k ∈ Z

B. x = $\frac{π}{6}$ + kπ, k ∈ Z

C. x = $- \frac{π}{4}$ + k2π, $- \frac{π}{6}$ + k2π, k ∈ Z

D. Tất cả sai

Xem đáp án

Đáp án D

Câu 20:

22/07/2024

Giải phương trình sin3x(cosx - 2sin3x) + cos3x(1 + sinx - 2cos3x) = 0

A. x = ± $\frac{π}{3}$ + k2π, k ∈ Z

B. x = $\frac{π}{4}$ + kπ, k ∈ Z

C. x = $- \frac{π}{4}$ + k2π, x = $- \frac{π}{6}$ + k2π,k ∈ Z

D. Vô nghiệm

Xem đáp án

Đáp án D

Vậy phương trình đã cho vô nghiệm

Lớp 1 - Cánh diều

Tiếng Anh 1

Toán lớp 1

Tiếng Việt lớp 1

Lớp 1 - Chân trời sáng tạo

Tiếng Anh 1

Toán lớp 1

Tiếng Việt lớp 1

Lớp 1 - Kết nối tri thức

Tiếng Anh 1

Toán lớp 1

Tiếng Việt lớp 1

Tiện ích

Đọc sách online

Bộ đề ôn hè lớp 1 lên lớp 2

Giáo án lớp 1

Lớp 2 - Kết nối tri thức

Toán lớp 2

Tiếng Việt lớp 2

Đạo đức lớp 2

Tự nhiên và Xã hội lớp 2

Hoạt động trải nghiệm lớp 2

Tiếng Anh lớp 2

Âm nhạc lớp 2

Lớp 2 - Cánh diều

Toán lớp 2

Tiếng Việt lớp 2

Hoạt động trải nghiệm lớp 2

Tự nhiên và Xã hội lớp 2

Tiếng Anh lớp 2

Âm nhạc lớp 2

Đạo đức lớp 2

Lớp 2 - Chân trời sáng tạo

Toán lớp 2

Tiếng Việt lớp 2

Đạo đức lớp 2

Tự nhiên và Xã hội lớp 2

Hoạt động trải nghiệm lớp 2

Tiếng Anh lớp 2

Âm nhạc lớp 2

Đề thi các môn lớp 2

Đề thi các môn lớp 2 - Kết nối tri thức

Đề thi các môn lớp 2 - Cánh diều

Đề thi các môn lớp 2 - Chân trời sáng tạo

Tiện ích

Đọc sách online

Bộ đề ôn hè lớp 2 lên lớp 3

Giáo án lớp 2

Lớp 3 - Kết nối tri thức

Toán lớp 3

Tiếng Anh lớp 3

Tiếng Việt lớp 3

Đạo đức lớp 3

Tự nhiên và Xã hội lớp 3

Hoạt động trải nghiệm lớp 3

Âm nhạc lớp 3

Tin học lớp 3

Giáo dục thể chất lớp 3

Công nghệ lớp 3

Lớp 3 - Cánh diều

Toán lớp 3

Tiếng Việt lớp 3

Tiếng Anh lớp 3

Đạo đức lớp 3

Tự nhiên và Xã hội lớp 3

Hoạt động trải nghiệm lớp 3

Âm nhạc lớp 3

Tin học lớp 3

Giáo dục thể chất lớp 3

Công nghệ lớp 3

Lớp 3 - Chân trời sáng tạo

Toán lớp 3

Tiếng Việt lớp 3

Tiếng Anh lớp 3

Đạo đức lớp 3

Tự nhiên và Xã hội lớp 3

Hoạt động trải nghiệm lớp 3

Âm nhạc lớp 3

Tin học lớp 3

Giáo dục thể chất lớp 3