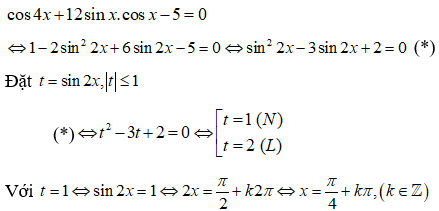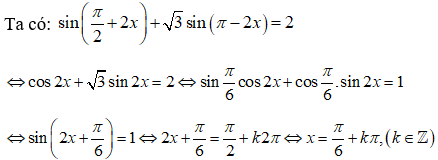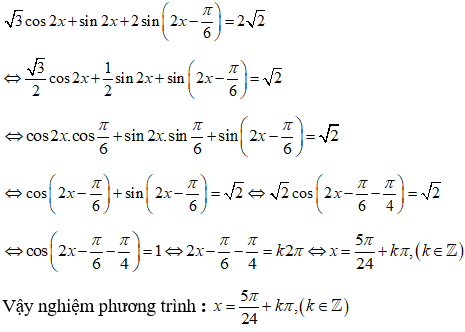20 câu hỏi trắc nghiệm thuộc 100 câu trắc nghiệm Phương trình lượng giác nâng cao (Đề số 4)

Câu 1:

21/07/2024

Giải phương trình: cos⁵x + x² = 0

A.

B.

C.

D.Vô nghiệm

Xem đáp án

Đáp án D

Câu 2:

19/07/2024

Tìm nghiệm x ∈ (0; π) của phương trình: 5cosx + sinx - 3 = $\sqrt{2}$ sin(2x + $\frac{π}{4}$ )

A. $x = \frac{π}{3}$

B.

C.

D. Vô nghiệm

Xem đáp án

Đáp án A

Câu 3:

23/07/2024

Tìm x ∈ (0; π) thỏa mãn phương trình $4 \sin^{2} \frac{x}{2} - \sqrt{3} \cos 2 x = 1 + 2 \cos^{2} (x - \frac{3 π}{4}) (1)$

A.

B.

C.

D.Tất cả sai

Xem đáp án

Đáp án D

+ Ta có: $k_{1} \in Z; x \in (0; π)$ nên

+ Ta có: $k_{2} \in Z; x \in (0; π)$ nên $k_{2} = 1 \Rightarrow x = \frac{5 π}{6}$

Vậy có tất cả 3 nghiệm thỏa mãn đầu bài

Câu 4:

23/07/2024

Giải các phương trình sau: 2cos3x.cosx - 4sin²2x + 1 = 0

A. x = ± $\frac{π}{3}$ + k2π, k ∈ Z

B. x = $\frac{π}{4}$ + kπ, k ∈ Z

C. x = $- \frac{π}{4}$ + k2π, x = $- \frac{π}{6}$ + k2π,k ∈ Z

D. x = ± $\frac{π}{6}$ + kπ

Xem đáp án

Đáp án D

Câu 5:

22/07/2024

Giải các phương trình sau:

A. x = ± $\frac{π}{6}$ + k2π, k ∈ Z

B. x = ± $\frac{5 π}{6}$ + k2π, k ∈ Z

C. x = $- \frac{π}{4}$ + k2π, x = $- \frac{π}{6}$ + k2π, k ∈ Z

D. Đáp án khác

Xem đáp án

Đáp án D

Khi đó, phương trình đã cho trở thành: $1 - t^{2} + 4 t = 4$

Câu 6:

20/07/2024

Giải phương trình: cos²( $\frac{π}{3}$ + x) + 4cos( $\frac{π}{6}$ – x) = 4

A. x = ± $\frac{π}{6}$ + k2π, k ∈ Z

B. x = ± $\frac{5 π}{6}$ + k2π, k ∈ Z

C. x = $\frac{π}{6}$ + k2π, k ∈ Z

D. Đáp án khác

Xem đáp án

Đáp án C

Câu 7:

23/07/2024

Giải phương trình: cos4x + 12sinx.cosx - 5 = 0

A. x = ± $\frac{π}{6}$ + k2π, k ∈ Z

B. x = ± $\frac{5 π}{6}$ + k2π, k ∈ Z

C. x = $\frac{π}{4}$ + k2π, k ∈ Z

D. Đáp án khác

Xem đáp án

Đáp án D

Câu 8:

18/07/2024

Giải phương trình: 4cos²(6x – 2) + 16cos²(1 – 3x) = 13

A. x = ± $\frac{π}{6}$ + k2π, k ∈ Z

B. x = ± $\frac{π}{6}$ + k $\frac{2 π}{3}$ , k ∈ Z

C. x = ± $\frac{π}{18}$ + k $\frac{2 π}{3}$ , k ∈ Z

D. Đáp án khác

Xem đáp án

Đáp án D

Câu 9:

23/07/2024

Họ nghiệm của phương trình 16(sin⁸x + cos⁸x) = 17cos²2x là:

A. x = $\frac{π}{8}$ + k $\frac{5 π}{4}$

B. x = $\frac{π}{8}$ + k $\frac{7 π}{4}$

C. x = $\frac{π}{8}$ + k $\frac{9 π}{4}$

D. x = $\frac{π}{8}$ + k $\frac{π}{4}$

Xem đáp án

Đáp án D

Nếu ta đặt $t = \sin^{2} 2 x; 0 \leq t \leq 1 \Rightarrow \cos^{2} 2 x = 1 - \sin^{2} 2 x = 1 - t$

Câu 10:

18/07/2024

Giải các phương trình sau: sin( $\frac{π}{2}$ + 2x) + $\sqrt{3}$ sin(π - 2x) = 2

A. $x = \pm \frac{π}{6} + k 2 π, k \in ℤ$

B. $x = \pm \frac{5 π}{6} + k 2 π, k \in ℤ$

C. $x = \frac{π}{4} + k 2 π, k \in ℤ$

D. $x = \frac{π}{6} + k π, k \in ℤ$

Xem đáp án

Đáp án D

Câu 11:

17/07/2024

Giải phương trình sau: $\sqrt{3} \cos 2 x + \sin 2 x + 2 \sin (2 x - \frac{π}{6}) = 2 \sqrt{2}$

A. x = ± $\frac{5 π}{24}$ + k2π

B. x = $\frac{5 π}{24}$ + k2π

C. x = $\frac{5 π}{24}$ + kπ

D. x = $\frac{π}{6}$ + kπ

Xem đáp án

Đáp án C

Câu 12:

20/07/2024

Một họ nghiệm của phương trình: $\sqrt{3} sinx + cosx = \frac{1}{cosx}$ là

A. x = k2π

B. x = $\frac{π}{3}$ + k2π

C. x = $\frac{π}{3}$ + kπ

D. x = $\frac{π}{6}$ + kπ

Xem đáp án

Đáp án C

Câu 13:

01/09/2024

Giải phương trình sau: $\frac{1}{cosx} + \frac{1}{\sin x} = \sqrt{2} \sin (x + \frac{π}{4})$

A. x = $\frac{π}{4}$ + kπ

B. x = $- \frac{π}{4}$ + kπ

C. x = $- \frac{π}{4}$ + kπ, kπ

D. x = $\frac{π}{6}$ + kπ

Xem đáp án

Đáp án B

Điều kiện: cosx ≠ 0, sinx ≠ 0

Với điều kiện trên, (*)

⇔ 2(sinx + cosx) = sin2x (cosx + sinx)

⇔ (sinx + cosx)(2 - sin2x) = 0

⇔ sinx + cosx = 0 ⇔ tan x = -1

⇔ x = -π/4 + kπ, k ∈ Z

So với điều kiện, nghiệm của phương trình là: x = -π/4 + kπ, k ∈ Z

*Giải thích

+ Sử dụng các hệ thức lượng giác cơ bản.
+ Sử dụng tính chất của giá trị lượng giác.
+ Sử dụng các hằng đẳng thức đáng nhớ.

Xem thêm các câu hỏi ôn tập Toán chọn lọc, hay khác:

Lý thuyết Toán 10 Bài 5. Giá trị lượng giác của một góc từ 00 đến 1800– Kết nối tri thức

Giải bài tập Toán 10 Bài 5: Giá trị lượng giác của một góc từ 0 độ đến 180 độ

Câu 14:

17/07/2024

Giải phương trình sau: tanx.sin²x – 2sin²x = 3(cos2x + sinx.cosx)

A. x = ± $\frac{π}{3}$ + kπ

B. x = $- \frac{π}{4}$ + kπ

C. x = $- \frac{π}{4}$ + kπ, kπ

D. Cả A và B đúng

Xem đáp án

Đáp án D

Câu 15:

07/11/2024

Giải phương trình sau: 5sinx – 2 = 3(1 – sinx)tan²x

A. x = $\frac{π}{6}$ + k2π, $k \in ℤ$

B. x = $\frac{5 π}{6}$ + kπ, $k \in ℤ$

C. x = $- \frac{5 π}{6}$ + kπ, $k \in ℤ$

D. Đáp án khác.

Xem đáp án

Đáp án đúng: D

*Lời giải:

Điều kiện: cosx $\neq$ 0 (*)

Phương trình $\Leftrightarrow 5 \sin x - 2 = 3. (1 - s inx) \frac{\sin^{2} x}{{cos}^{2} x}$

$\Leftrightarrow 5 \sin x - 2 = 3. (1 - s inx) \frac{\sin^{2} x}{1 - \sin^{2} x}$

$\Leftrightarrow 5 \sin x - 2 = \frac{3 \sin^{2} x}{1 + \sin x}$

$\Leftrightarrow 2 \sin^{2} x + 3 \sin x - 2 = 0$

$\Leftrightarrow [\begin{array}{l} s inx = \frac{1}{2} (T M) \\ s inx = - 2 (L) \end{array}$

Xét $s inx = \frac{1}{2} \Leftrightarrow [\begin{array}{l} x = \frac{π}{6} + k 2 π \\ x = \frac{5 π}{6} + k 2 π \end{array}, k \in ℤ$ (thỏa mãn điều kiện (*))

Vậy nghiệm của phương trình là: $x = \frac{π}{6} + k 2 π$ và $x = \frac{5 π}{6} + k 2 π$ .

*Phương pháp giải:

- đối với hàm tan và cot ta nên tìm điều kiện xác định trước

- dùng các công thức lượng giác biến đổi 2 vế của phương trình, giải và tìm ra nghiệm

*Lý thuyết và các dạng bài tập về phương trình lượng giác cơ bản:

Phương trình cosx=a

- Trường hợp |a| > 1

Phương trình cosx = a vô nghiệm vì $|cosx| \leq 1$ với mọi x.

- Trường hợp $|a| \leq 1$ .

Gọi α là số đo radian của một cung lượng giác. Khi đó, phương trình cosx = a có các nghiệm là: $x = \pm α + k 2 π; k \in ℤ$

Phương trình tanx=a

- Điều kiện xác định của phương trình là $x \neq \frac{π}{2} + k π; k \in ℤ$

Kí hiệu x = arctana (đọc là ac– tang– a; nghĩa là cung có tang bằng a). Khi đó, nghiệm của phương trình tanx = a là: $x = \arctan a + k π; k \in ℤ$

+) Phương trình tanx = tanα, với α là một số cho trước, có các nghiệm là: $x = α + k π; k \in ℤ$

Tổng quát; tan f(x) = tan g(x) $\Rightarrow f (x) = g (x) + k π; k \in ℤ$ .

+) Phương trình tanx = tanβ⁰ có các nghiệm là: $x = β^{0} + k {.180}^{0}; k \in ℤ$ .

Hai phương trình được gọi là tương đương khi chúng có cùng tập nghiệm.

Nếu phương trình f(x) =0 tương đương với phương trình g(x) =0 thì ta viết $f (x) = 0 \Leftrightarrow g (x) = 0$

*Chú ý: Hai phương trình vô nghiệm là hai phương trình tương đương.

Phương trình bậc nhất đối với một hàm số lượng giác là phương trình có dạng:

at + b = 0 (1)

Trong đó; a, b là các hằng số (a ≠ 0) và t là một trong các hàm số lượng giác.

Phương trình đưa về phương trình bậc nhất đối với một hàm số lượng giác.

- Phương pháp:

Sử dụng các công thức biến đổi lượng giác đã được học để đưa về phương trình bậc nhất đối với hàm số lượng giác hoặc đưa về phương trình tích để giải phương trình.

Phương trình bậc hai với hàm số lượng giác

Định nghĩa.

Phương trình bậc hai đối với một hàm số lượng giác là phương trình có dạng:

at² + bt + c = 0

Trong đó a; b; c là các hằng số (a ≠ 0) và t là một trong các hàm số lượng giác.

Xem thêm các bài viết liên quan hay, chi tiết:

Lý thuyết Phương trình lượng giác cơ bản – Toán 11

Bài tập Phương trình lượng giác cơ bản Toán 11

Trắc nghiệm Phương trình lượng giác cơ bản (có đáp án)– Toán 11

Câu 16:

19/07/2024

Giải phương trình sau: $\frac{\cos 2 x + 3 \cot 2 x + \sin 4 x}{\cot 2 x - \cos 2 x} = 2$

A. x = $- \frac{π}{12}$ + k2π

B. x = $\frac{5 π}{12}$ + kπ

C. x = $- \frac{π}{12}$ + kπ; x = $- \frac{5 π}{12}$ + kπ

D. Cả A và B đúng

Xem đáp án

Đáp án C

Chú ý: Hai họ nghiệm $x = \frac{- 5 π}{12} + k π$ và $x = \frac{7 π}{12} + k π$ là trùng nhau .

Câu 17:

19/07/2024

Giải phương trình sau: $\frac{4 \sin^{2} 2 x + 6 \sin^{2} x - 3 \cos 2 x - 9}{cosx} = 0$

A. x = $- \frac{π}{3}$ + kπ

B. x = $\frac{π}{3}$ + kπ

C. x = $- \frac{π}{12}$ + kπ, $- \frac{5 π}{12}$ kπ

D. Cả A và B đúng

Xem đáp án

Đáp án D

Điều kiện : cosx $\neq 0$

Câu 18:

21/07/2024

Giải phương trình sau: $\frac{cosx (cosx + 2 sinx) + 3 sinx (sinx + \sqrt{2})}{\sin 2 x - 1} = 1$

A. x = $- \frac{π}{4}$ + k2π

B. x = $- \frac{3 π}{4}$ + k2π

C. x = ± $\frac{π}{4}$ + kπ

D. Cả A và B đúng

Xem đáp án

Đáp án A

Câu 19:

23/07/2024

Giải phương trình sau: $\frac{\sin^{2} 2 x - 2}{\sin^{2} 2 x - 4 \cos^{2} x} = \tan^{2} x$

A. x = $- \frac{π}{4}$ + k2π

B. x = $- \frac{π}{4}$ + k $\frac{π}{2}$

C. x = $- \frac{π}{4}$ + kπ; $\frac{π}{4}$ + kπ

D. Đáp án khác

Xem đáp án

Đáp án D

Câu 20:

18/07/2024

Giải phương trình sau: $\frac{1 + \sin 2 x + \cos 2 x}{1 + \cot^{2} x} = \sqrt{2} sinx . \sin 2 x$

A. $x = - \frac{π}{4} + k 2 π, k \in ℤ$

B. $x = - \frac{π}{4} + k \frac{π}{2}, k \in ℤ$

C. $x = \frac{π}{2} + k π, x = \frac{π}{4} + k 2 π, k \in ℤ$

D. $x = \frac{π}{2} + k π, k \in ℤ$

Xem đáp án

Đáp án C

$s inx \neq 0 \Leftrightarrow x \neq k π, k \in ℤ$

Xét phương trình: $\frac{1 + \sin 2 x + \cos 2 x}{1 + \cot^{2} x} = \sqrt{2} s inx . \sin 2 x$

$\Leftrightarrow \sin^{2} x (1 + \sin 2 x + \cos 2 x) = 2 \sqrt{2} s {in}^{2} x . c os x$

$\Leftrightarrow 1 + \sin 2 x + \cos 2 x = 2 \sqrt{2} c os x$

$\Leftrightarrow 1 + \sin 2 x + \cos 2 x = 2 \sqrt{2} c os x$ (do $sinx \neq 0$ )

$\Leftrightarrow 1 + 2 \sin x . c o s x + 2 \cos^{2} x - 1 - 2 \sqrt{2} c os x = 0$

$\Leftrightarrow 2 \sin x . c o s x + 2 \cos^{2} x - 2 \sqrt{2} c os x = 0$

$\Leftrightarrow c os x (2 \sin x + 2 \cos x - 2 \sqrt{2}) = 0$

$\Leftrightarrow [\begin{array}{l} c os x = 0 \\ 2 \sin x + 2 \cos x - 2 \sqrt{2} = 0 \end{array}$

$\Leftrightarrow [\begin{array}{l} c os x = 0 \\ \sin x + \cos x = \sqrt{2} \end{array}$

$\Leftrightarrow [\begin{array}{l} c os x = 0 \\ \sin (x + \frac{π}{4}) = 1 \end{array}$

$\Leftrightarrow [\begin{array}{l} x = \frac{π}{2} + k π \\ x + \frac{π}{4} = \frac{π}{2} + k 2 π \end{array}, k \in ℤ$

$\Leftrightarrow [\begin{array}{l} x = \frac{π}{2} + k π \\ x = \frac{π}{4} + k 2 π \end{array}, k \in ℤ$

Vậy nghiệm của phương trình là: $x = \frac{π}{2} + k π, x = \frac{π}{4} + k 2 π, k \in ℤ$ .

Lớp 1 - Cánh diều

Tiếng Anh 1

Toán lớp 1

Tiếng Việt lớp 1

Lớp 1 - Chân trời sáng tạo

Tiếng Anh 1

Toán lớp 1

Tiếng Việt lớp 1

Lớp 1 - Kết nối tri thức

Tiếng Anh 1

Toán lớp 1

Tiếng Việt lớp 1

Tiện ích

Đọc sách online

Bộ đề ôn hè lớp 1 lên lớp 2

Giáo án lớp 1

Lớp 2 - Kết nối tri thức

Toán lớp 2

Tiếng Việt lớp 2

Đạo đức lớp 2

Tự nhiên và Xã hội lớp 2

Hoạt động trải nghiệm lớp 2

Tiếng Anh lớp 2

Âm nhạc lớp 2

Lớp 2 - Cánh diều

Toán lớp 2

Tiếng Việt lớp 2

Hoạt động trải nghiệm lớp 2

Tự nhiên và Xã hội lớp 2

Tiếng Anh lớp 2

Âm nhạc lớp 2

Đạo đức lớp 2

Lớp 2 - Chân trời sáng tạo

Toán lớp 2

Tiếng Việt lớp 2

Đạo đức lớp 2

Tự nhiên và Xã hội lớp 2

Hoạt động trải nghiệm lớp 2

Tiếng Anh lớp 2

Âm nhạc lớp 2

Đề thi các môn lớp 2

Đề thi các môn lớp 2 - Kết nối tri thức

Đề thi các môn lớp 2 - Cánh diều

Đề thi các môn lớp 2 - Chân trời sáng tạo

Tiện ích

Đọc sách online

Bộ đề ôn hè lớp 2 lên lớp 3

Giáo án lớp 2

Lớp 3 - Kết nối tri thức

Toán lớp 3

Tiếng Anh lớp 3

Tiếng Việt lớp 3

Đạo đức lớp 3

Tự nhiên và Xã hội lớp 3

Hoạt động trải nghiệm lớp 3

Âm nhạc lớp 3

Tin học lớp 3

Giáo dục thể chất lớp 3

Công nghệ lớp 3

Lớp 3 - Cánh diều

Toán lớp 3

Tiếng Việt lớp 3

Tiếng Anh lớp 3

Đạo đức lớp 3

Tự nhiên và Xã hội lớp 3

Hoạt động trải nghiệm lớp 3

Âm nhạc lớp 3

Tin học lớp 3

Giáo dục thể chất lớp 3

Công nghệ lớp 3

Lớp 3 - Chân trời sáng tạo

Toán lớp 3

Tiếng Việt lớp 3

Tiếng Anh lớp 3

Đạo đức lớp 3

Tự nhiên và Xã hội lớp 3

Hoạt động trải nghiệm lớp 3

Âm nhạc lớp 3

Tin học lớp 3

Giáo dục thể chất lớp 3