100 câu trắc nghiệm Phương trình lượng giác nâng cao
100 câu trắc nghiệm Phương trình lượng giác nâng cao (Đề số 2)
-
1920 lượt thi
-
20 câu hỏi
-
20 phút
Danh sách câu hỏi
Câu 1:
17/07/2024Hàm số y = 2cos2 x + 3cos3x + 8cos4x tuần hoàn với chu kì
 Xem đáp án
Xem đáp án
Đáp án B
+ Hàm số y = 9/4cos x tuần hoàn với chu kì 2π.
+ Hàm số y = 5cos 2x tuần hoàn với chu kì 2π/2 = π .
+ Hàm số y = 3/4 cos 3x tuần hoàn với chu kì 2π/3.
+ Hàm số y = cos 4x tuần hoàn với chu kì 2π/4 = π/2.
+ Do đó hàm số y = 2 cos2 x + 3cos3x + 8cos4x là hàm tuần hoàn với chu kì 2π.
Chú ý:

Câu 2:
22/07/2024Hàm số y = 2sin2x + 4cos2x + 6sinxcosx tuần hoàn với chu kì:
 Xem đáp án
Xem đáp án
Đáp án C
+ Hàm số y = 3sin 2x tuần hoàn với chu kì 2π/2 = π.
+ Hàm số y = cos 2x tuần hoàn với chu kì 2π/2 = π.
+ Do đó hàm số y = 2sin2x + 4cos2x + 6sinxcosx là hàm tuần hoàn với chu kì π
Câu 3:
17/07/2024Tìm tất cả các giá trị của tham số m để hàm số sau chỉ nhận giá trị dương :
y = (3sinx - 4cosx)2 - 6sinx + 8cosx + 2m - 1
 Xem đáp án
Xem đáp án
Đáp án B
Đặt t = 3sin x - 4 cos x => -5 ≤ t ≤ 5
Ta có: y = t2 – 2t + 2m – 1 = (t – 1)2 + 2m - 2
Với mọi t ta có (t – 1)2 ≥ 0 nên y ≥ 2m - 2 => min y = 2m - 2
Hàm số chỉ nhận giá trị dương ⇔ y > 0 ∀x ∈ R ⇔ min y > 0
⇔ 2m - 2 > 0 ⇔ m > 1

Câu 4:
22/07/2024Tìm m để hàm số y = xác định với mọi x
 Xem đáp án
Xem đáp án
Đáp án D
Hàm số xác định với mọi x
⇔ 2sin2x + 4sinx cosx – (3 + 2m)cos2x + 2 0 ∀x ∈ R (1)
cos x = 0 => (1) đúng
cos x ≠ 0 khi đó ta có: (1) ⇔ 2tan2x + 4tanx – (3 + 2m) + 2(1 + tan2x) ≥ 0
⇔ 4tan2x + 4tanx ≥ 1 + 2m ∀x ∈ R
⇔ (2tanx + 1)2 ≥ 2 + 2m ∀x ∈ R ⇔ 2 + 2m ≤ 0 ⇔ m ≤ -1
Câu 6:
18/07/2024Tìm m để các bất phương trình sau đúng với mọi x:
(3sinx – 4cosx)2 – 6sinx + 8cosx ≥ 2m - 1
 Xem đáp án
Xem đáp án
Đáp án D
Đặt t = 3sin x - 4cos x
Ta có: y = (3sin x – 4cos x)2 – 6sin x + 8cos x
= t2 – 2t = (t – 1)2 -1
Với mọi t ta có; => min y = -1
Suy ra yêu cầu bài toán -1 ≥ 2m - 1 ⇔ m ≤ 0.
Câu 8:
17/07/2024Tìm giá trị lớn nhất của hàm số sau y = sinx - trong khoảng 0 < x < π
 Xem đáp án
Xem đáp án
Đáp án B
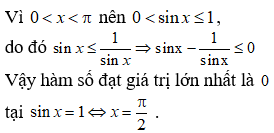
Câu 10:
20/10/2024Tìm giá trị lớn nhất, giá trị nhỏ nhất của các hàm số sau: y = sin6x + cos6x
 Xem đáp án
Xem đáp án
Đáp án đúng: C
* Phương pháp giải
- Dùng công thức :
sin2
α+cos2α=1
- Và công thức: sin2x = 2 sinxcosx để biến đổi vài giải bài toán:
+ giá trị của sinx nằm trong đoạn từ 0 đến 1. từ đó giải ra sẽ nhìn thấy min và max
* Lời giải
* Lý thuyết nắm thêm và các dạng bài toán về phương trình lượng giác:
Phương trình bậc nhất đối với một hàm số lượng giác là phương trình có dạng:
at + b = 0 (1)
Trong đó; a, b là các hằng số (a ≠ 0) và t là một trong các hàm số lượng giác.
- Phương pháp giải: Chuyển vế rồi chia hai vế của phương trình (1) cho a, ta đưa phương trình (1) về phương trình lượng giác cơ bản.
Phương trình đưa về phương trình bậc nhất đối với một hàm số lượng giác.
- Phương pháp: Sử dụng các công thức biến đổi lượng giác đã được học để đưa về phương trình bậc nhất đối với hàm số lượng giác hoặc đưa về phương trình tích để giải phương trình.
Phương trình bậc hai đối với một hàm số lượng giác là phương trình có dạng:
at2 + bt + c = 0
Trong đó a; b; c là các hằng số (a ≠ 0) và t là một trong các hàm số lượng giác.
-Phương pháp giải: Đặt biểu thức lượng giác làm ẩn phụ và đặt điều kiện cho ẩn phụ (nếu có) rồi giải phương trình theo ẩn phụ này. Cuối cùng ta đưa về việc giải các phương trình lượng giác cơ bản.
Phương trình đưa về dạng phương trình bậc hai đối với một hàm số lượng giác.
- Phương pháp: Sử dụng các công thức lượng giác đã học để biến đổi đưa về dạng phương trình bậc hai đối với một hàm số lượng giác.
PHƯƠNG TRÌNH BẬC NHẤT ĐỐI VỚI SINX VÀ COSX
Công thức biến đổi biểu thức a.sinx + b.cosx
Ta có công thức biến đổi sau:
Trong đó;
Phương trình dạng: asinx + b.cosx = c.
Xét phương trình: asinx + bcosx = c (2)
Với a; b; c ; a, b không đồng thời bằng 0.
- Nếu a = 0 ; b ≠ 0 hoặc a ≠ 0; b = 0 phương trình (2) có thể đưa ngay về phương trình lượng giác cơ bản.
- Nếu a ≠ 0; b ≠ 0, ta áp dụng công thức (1).
Xem thêm các bài viết liên quan hay, chi tiết khác:
Lý thuyết Một số phương trình lượng giác thường gặp (2024) và cách giải các dạng bài tập
50 Bài tập Phương trình lượng giác cơ bản Toán 11 mới nhất
Toán 11 Bài 2 giải bài tập SGK: Phương trình lượng giác cơ bản
Câu 11:
21/07/2024Tìm giá trị lớn nhất, giá trị nhỏ nhất của các hàm số sau y =
 Xem đáp án
Xem đáp án
Đáp án B
Câu 12:
22/07/2024Tìm giá trị lớn nhất, giá trị nhỏ nhất của các hàm số sau y = tanx, x ∈ [; ]
 Xem đáp án
Xem đáp án
Đáp án D

Câu 13:
17/07/2024Cho hàm số sau y = tan2x – tanx + 2, x ∈ [;]. Chọn khẳng định đúng
 Xem đáp án
Xem đáp án
Đáp án B
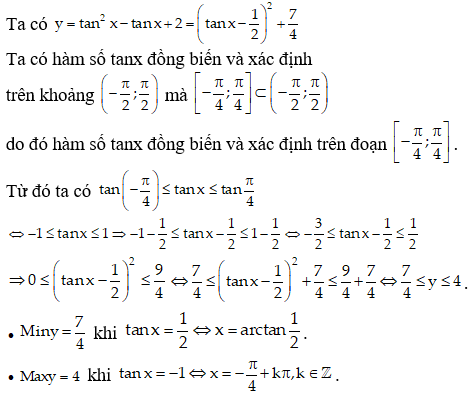
Câu 14:
18/07/2024Cho hàm số sau chọn khẳng định đúng: y = 2sin2x – sin2x + 7
 Xem đáp án
Xem đáp án
Đáp án A
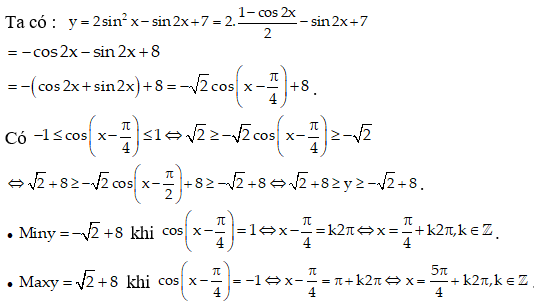
Câu 16:
17/07/2024Khẳng định nào sau đây là đúng ?
 Xem đáp án
Xem đáp án
Đáp án B
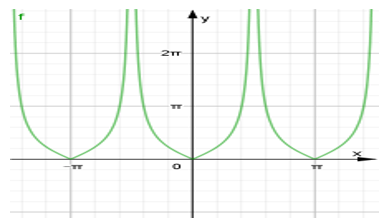
Ta được đồ thị như hình vẽ trên.
Ta thấy hàm số y = |tan x| nghịch biến trên (-π/2; 0) và đồng biến trên (0; π/2) . Nên ta loại A và D.
Với B ta có f(-x) = |tan(-x)| = | - tan x |= |tan x| = f(x) => hàm số y = |tan x| là hàm số chẵn.
Hàm số chẵn, nhận trục Oy làm trục đối xứng, không nhận tâm O làm tâm đối xứng.
Nên phương án C là sai
Bài thi liên quan
-
100 câu trắc nghiệm Phương trình lượng giác nâng cao (Đề số 1 )
-
20 câu hỏi
-
20 phút
-
-
100 câu trắc nghiệm Phương trình lượng giác nâng cao (Đề số 3)
-
20 câu hỏi
-
20 phút
-
-
100 câu trắc nghiệm Phương trình lượng giác nâng cao (Đề số 4)
-
20 câu hỏi
-
20 phút
-
-
100 câu trắc nghiệm Phương trình lượng giác nâng cao (Đề số 5)
-
20 câu hỏi
-
20 phút
-
Có thể bạn quan tâm
- Trắc nghiệm Ôn tập chương 1 (có đáp án) (716 lượt thi)
- 100 câu trắc nghiệm Hàm số lượng giác cơ bản (1354 lượt thi)
- 100 câu trắc nghiệm Phương trình lượng giác nâng cao (1919 lượt thi)
- Trắc nghiệm Chương 1: Hàm số lượng giác và phương trình lượng giác có đáp án (584 lượt thi)
Các bài thi hot trong chương
- Trắc nghiệm Hàm số lượng giác (có đáp án) (1443 lượt thi)
- Trắc nghiệm Phương trình lượng giác cơ bản (có đáp án) (819 lượt thi)
- Trắc nghiệm Một số phương trình lượng giác thường gặp (có đáp án) (654 lượt thi)
- Một số phương trình lượng giác thường gặp có đáp án (Vận dụng) (589 lượt thi)
- Trắc nghiệm Phương trình lượng giác cơ bản có đáp án (Thông hiểu) (587 lượt thi)
- Trắc nghiệm Hàm số lượng giác có đáp án (Nhận biết) (526 lượt thi)
- Trắc nghiệm Hàm số lượng giác có đáp án (Thông hiểu) (439 lượt thi)
- Trắc nghiệm Hàm số lượng giác có đáp án (389 lượt thi)
- Trắc nghiệm Hàm số lượng giác có đáp án (Vận dụng) (380 lượt thi)
- Trắc nghiệm Phương trình lượng giác cơ bản có đáp án (Vận dụng) (375 lượt thi)



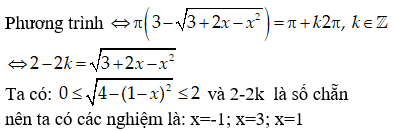
![Tìm tổng các nghiệm của phương trình: sin(5x + pi/3) = cos(2x - pi/3) trên [0; pi] (ảnh 1)](https://video.vietjack.com/upload1/quiz_source1/2019/09/p2-c20-1567704196.png)