Giải Toán 9 (Cánh diều): Bài tập cuối chương 9

Giải bài tập Toán 9 Bài tập cuối chương 9

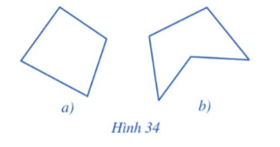
Bài 1 trang 90 Toán 9 Tập 2: Quan sát các đa giác ở Hình 34 và cho biết đa giác nào là đa giác lồi.

Lời giải:

Đa giác trong Hình 34a) là đa giác lồi vì đa giác này luôn nằm về một phía của đường thẳng chứa một cạnh bất kì của đa giác đó.

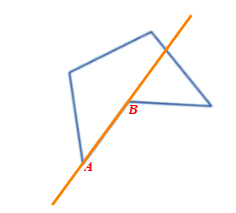
Đa giác trong Hình 34b) không phải là đa giác lồi vì đa giác không nằm về một phía của của đường thẳng chứa cạnh bất kì, chẳng hạn cạnh AB như hình vẽ sau:

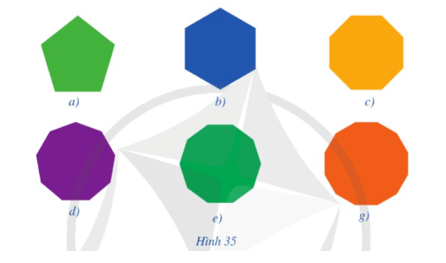
Bài 2 trang 90 Toán 9 Tập 2: Cho các vật thể có dạng đa giác đều như ở Hình 35. Gọi tên từng đa giác đều đó.

Lời giải:

Hình 35a) là ngũ giác đều.

Hình 35b) là lục giác đều.

Hình 35c) là bát giác đều (đa giác đều tám cạnh).

Hình 35d) là cửu giác đều (đa giác đều chín cạnh).

Hình 35e) là thập giác đều (đa giác đều mười cạnh).

Hình 35g) là đa giác đều mười hai cạnh.

Bài 3 trang 90 Toán 9 Tập 2: Mỗi phát biểu sau đây có đúng hay không? Vì sao?

a) Đa giác luôn nằm về một phía của đường thẳng chứa một cạnh bất kì của đa giác đó là đa giác lồi.

b) Tứ giác có tất cả các cạnh bằng nhau là tứ giác đều.

c) Tứ giác có tất cả các góc bằng nhau là tứ giác đều.

Lời giải:

Phát biểu a) là đúng theo định nghĩa đa giác lồi là đa giác luôn nằm về một phía của đường thẳng chứa một cạnh bất kỳ của đa giác đó.

Phát biểu b) và c) là sai vì tứ giác đều là tứ giác có tất cả các cạnh bằng nhau và tất cả các góc bằng nhau.

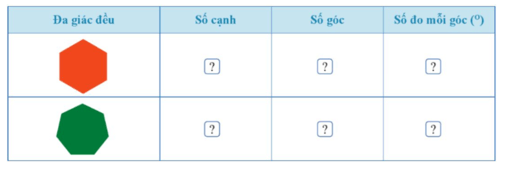
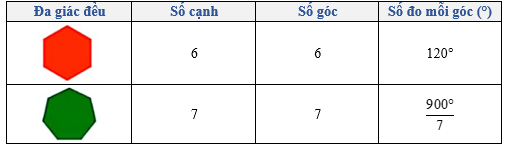
Bài 4 trang 90 Toán 9 Tập 2: Quan sát từng đa giác đều và tìm số thích hợp cho ? trong bảng sau:

Lời giải:

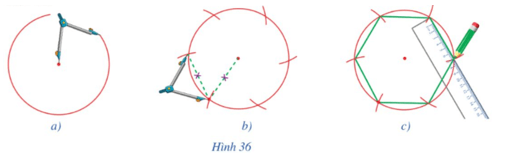
Bài 5 trang 91 Toán 9 Tập 2: Quan sát các hình 36a, 36b, 36c và dùng compa, thước thẳng để vẽ lục giác đều theo cách đó.

Lời giải:

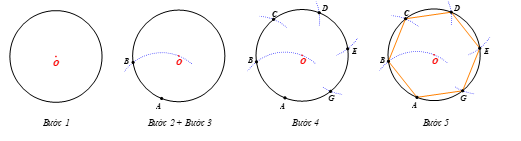
– Bước 1: Dùng compa vẽ đường tròn (O) có bán kính bất kì.

– Bước 2: Lấy điểm A bất kì nằm trên đường tròn (O).

– Bước 3: Vẽ cung tròn tâm A bán kính AO, cắt đường tròn (O) tại điểm B.

– Bước 4: Lặp lại Bước 3 ở trên, ta được các điểm C, D, E, G

– Bước 5: Dùng thước nối các đoạn thẳng AB, BC, CD, DE, EG, GA ta được hình lục giác đều ABCDEG.

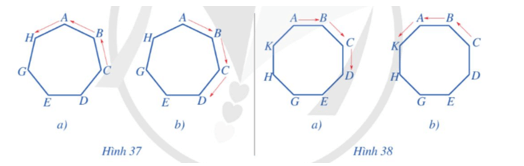
Bài 6 trang 91 Toán 9 Tập 2: a) Ở Hình 37a, ta thực hiện phép quay giữ nguyên hình đa giác đều có 7 cạnh ABCDEGH và biến các điểm A, B, C, D, E, G, H lần lượt thành các điểm H, A, B, C, D, E, G. Phép quay đó là phép quay nào?

b) Ở Hình 37b, ta thực hiện phép quay giữ nguyên hình đa giác đều có 7 cạnh ABCDEGH và biến các điểm A, B, C, D, E, G, H lần lượt thành các điểm B, C, D, E, G, H, A. Phép quay đó là phép quay nào?

c) Ở Hình 38a, ta thực hiện phép quay giữ nguyên hình đa giác đều có 8 cạnh ABCDEGHK và biến các điểm A, B, C, D, E, G, H, K lần lượt thành các điểm B, C, D, E, G, H, K, A. Phép quay đó là phép quay nào?

d) Ở Hình 38b, ta thực hiện phép quay giữ nguyên hình đa giác đều có 8 cạnh ABCDEGHK và biến các điểm A, B, C, D, E, G, H, K lần lượt thành các điểm K, A, B, C, D, E, G, H. Phép quay đó là phép quay nào?

Lời giải:

a) Ở Hình 37a, ta thực hiện phép quay ngược chiều giữ nguyên hình đa giác đều ABCDEGH (có 7 cạnh) và biến các điểm A, B, C, D, E, G, H lần lượt thành các điểm H, A, B, C, D, E, G. Phép quay đó là phép quay ngược chiều $\frac{360°}{7}$ tâm O.

b) Ở Hình 37b, ta thực hiện phép quay thuận chiều giữ nguyên hình đa giác đều ABCDEGH (có 7 cạnh) và biến các điểm A, B, C, D, E, G, H lần lượt thành các điểm B, C, D, E, G, H, A. Phép quay đó là phép quay thuận chiều $\frac{360°}{7}$ tâm O.

c) Ở Hình 38a, ta thực hiện phép quay thuận chiều giữ nguyên hình đa giác đều ABCDEGHK và biến các điểm A, B, C, D, E, G, H, K lần lượt thành các điểm B, C, D, E, G, H, K, A. Phép quay đó là phép quay thuận chiều $\frac{360°}{8}=45°$ tâm O.

d) Ở Hình 38b, ta thực hiện phép quay ngược chiều giữ nguyên hình đa giác đều ABCDEGHK và biến các điểm A, B, C, D, E, G, H, K lần lượt thành các điểm K, A, B, C, D, E, G, H. Phép quay đó là phép quay ngược chiều $\frac{360°}{8}=45°$ tâm O.

Bài 7 trang 91 Toán 9 Tập 2: Hãy tìm hiểu và chỉ ra những vật thể trong thực tiễn mà cấu trúc của nó có dạng hình đa giác đều.

Lời giải:

– Giá, kệ treo trang trí có hình tam giác đều, hình vuông, ngũ giác đều, lục giác đều;

– Hộp mứt tết, bề mặt tổ ong có hình lục giác đều;

…

Xem thêm Lời giải bài tập Toán 9 Cánh diều hay, chi tiết khác:

Bài 1: Hình trụ

Bài 2: Hình nón

Bài 3: Hình cầu

Bài tập cuối chương 10

Chủ đề 3: Tạo đồ dùng dạng hình nón, hình trụ