Giải Toán 9 Bài 1 (Cánh diều): Đường tròn ngoại tiếp tam giác. Đường tròn nội tiếp tam giác

Giải bài tập Toán 9 Bài 1: Đường tròn ngoại tiếp tam giác. Đường tròn nội tiếp tam giác

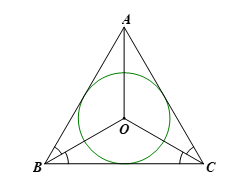
Khởi động trang 68 Toán 9 Tập 2: Trong thiết kế logo ở Hình 1, đường tròn đi qua ba đỉnh của tam giác.

Đường tròn đi qua ba đỉnh của tam giác được gọi là gì?

Lời giải:

Sau bài học này, chúng ta sẽ trả lời được câu hỏi trên như sau:

Đường tròn đi qua ba đỉnh của tam giác được gọi là đường tròn ngoại tiếp tam giác đó.I. Đường tròn ngoại tiếp tam giác

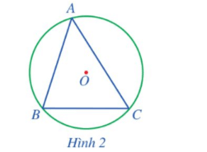
Luyện tập 1 trang 69 Toán 9 Tập 2: Quan sát Hình 4 và cho biết trong hai đường tròn (O) và (I), đường tròn nào ngoại tiếp tam giác ABC, đường tròn nào ngoại tiếp tam giác ABD?

Lời giải:

⦁ Đường tròn (O) là đường tròn ngoại tiếp tam giác ABC vì nó đi qua ba đỉnh A, B, C của tam giác ABC.

⦁ Đường tròn (I) là đường tròn ngoại tiếp tam giác ABD vì nó đi qua ba đỉnh A, B, D của tam giác ABD.

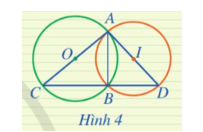
Hoạt động 1 trang 68 Toán 9 Tập 2: Cho biết các đỉnh của tam giác ABC (Hình 2) có thuộc đường tròn (O) hay không

Lời giải:

Các đỉnh A, B, C của tam giác ABC đều thuộc đường tròn (O).

Luyện tập 1 trang 69 Toán 9 Tập 2: Quan sát Hình 4 và cho biết trong hai đường tròn (O) và (I), đường tròn nào ngoại tiếp tam giác ABC, đường tròn nào ngoại tiếp tam giác ABD?

Lời giải:

⦁ Đường tròn (O) là đường tròn ngoại tiếp tam giác ABC vì nó đi qua ba đỉnh A, B, C của tam giác ABC.

⦁ Đường tròn (I) là đường tròn ngoại tiếp tam giác ABD vì nó đi qua ba đỉnh A, B, D của tam giác ABD.

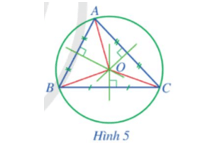
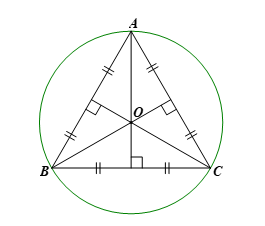
Hoạt động 2 trang 69 Toán 9 Tập 2: Cho tam giác ABC có O là giao điểm của ba đường trung trực (Hình 5).

a) Các đoạn thẳng OA, OB và OC có bằng nhau hay không?

b) Đặt R = OA. Đường tròn (O; R) có phải là đường tròn ngoại tiếp tam giác ABC hay không? Vì sao?

Lời giải:

a) Vì O là giao điểm của ba đường trung trực của tam giác ABC nên điểm O cách đều ba đỉnh của tam giác ABC.

Do đó OA = OB = OC.

b) Ta có OA = OB = OC = R nên ba điểm A, B, C cùng nằm trên đường tròn (O; R) hay đường tròn (O; R) đi qua ba đỉnh của tam giác.

Vậy đường tròn (O; R) là đường tròn ngoại tiếp tam giác ABC.

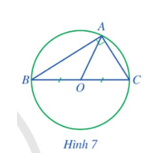
Hoạt động 3 trang 70 Toán 9 Tập 2: Cho tam giác ABC vuông tại A. Gọi O là trung điểm của BC (Hình 7). Đường tròn (O; OB) có phải là đường tròn ngoại tiếp của tam giác ABC hay không?

Lời giải:

Xét tam giác ABC vuông tại A có AO là đường trung tuyến ứng với cạnh huyền BC nên $AO=\frac{1}{2}BC.$

Mà O là trung điểm của BC nên $OB=OC=\frac{1}{2}BC.$

Do đó $OA=OB=OC=\frac{1}{2}BC.$

Vậy đường tròn (O; OB) đi qua các điểm A, B, C của tam giác ABC nên (O; OB) là đường tròn ngoại tiếp của tam giác ABC.

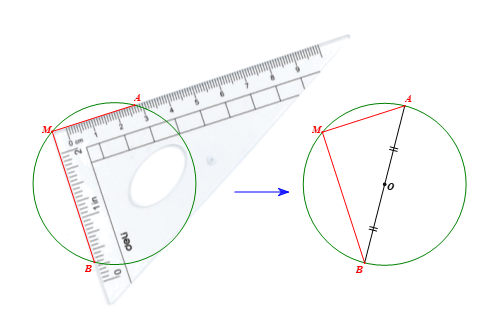
Luyện tập 2 trang 70 Toán 9 Tập 2: Nêu cách sử dụng ê ke để xác định tâm của một đường tròn bất kì khi chưa biết tâm của nó.

Lời giải:

Cách sử dụng ê ke để xác định tâm của một đường tròn bất kì khi chưa biết tâm của nó:

Bước 1. Lấy một điểm M bất kì trên đường tròn.

Bước 2. Đặt đỉnh vuông của ê ke trùng với điểm M.

Bước 3. Kẻ hai đường thẳng đi qua hai cạnh góc vuông của ê kê, hai đường thẳng này cắt đường tròn lần lượt tại hai điểm A, B (khác điểm M).

Bước 4. Nối đoạn thẳng AB, khi đó AB là đường kính của đường tròn.

Bước 5. Lấy O là trung điểm của AB, khi đó O là tâm của đường tròn đã cho.

Thật vậy, ∆MAB vuông tại M nên đường tròn ngoại tiếp tam giác MAB có tâm là trung điểm O của cạnh huyền AB.

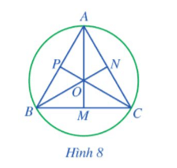
Hoạt động 4 trang 70 Toán 9 Tập 2: Cho tam giác đều ABC cạnh a, ba đường trung tuyến AM, BN, CP cắt nhau tại trọng tâm O (Hình 8).

a) AM, BN, CP có là các đường trung trực của tam giác ABC hay không?

b) Điểm O có là tâm đường tròn ngoại tiếp tam giác ABC hay không?

c) Tính AM theo a.

d) Tính OA theo a.

Lời giải:

a) Vì ∆ABC đều nên ba đường trung tuyến AM, BN, CP cũng đồng thời là các đường trung trực của tam giác ABC.

b) Vì ba đường trung trực AM, BN, CP của tam giác ABC cắt nhau tại điểm O nên O là tâm đường tròn ngoại tiếp tam giác ABC.

c) Vì ∆ABC đều nên $\widehat{ABM}=\widehat{ABC}=60°.$

Xét ∆ABM vuông tại M, ta có:

$AM=AB\cdot sin\widehat{ABM}=a\cdot \sin 60°=\frac{a\sqrt{3}}{2}.$

d) Tam giác ABC có AM là đường trung tuyến và O là trọng tâm của tam giác.

Do đó $AO=\frac{2}{3}AM=\frac{2}{3}\cdot \frac{a\sqrt{3}}{2}=\frac{a\sqrt{3}}{3}.$

Vậy $AO=\frac{a\sqrt{3}}{3}.$

Luyện tập 3 trang 71 Toán 9 Tập 2: Tam giác đều ABC nội tiếp đường tròn (O; 2 cm). Tính AB.

Lời giải:

Giả sử tam giác ABC đều có cạnh bằng a. Khi đó AB = a.

Vì tam giác đều ABC nội tiếp đường tròn (O; 2 cm) nên O là trọng tâm của tam giác và bán kính đường tròn ngoại tiếp (O; 2 cm) là $AO=\frac{a\sqrt{3}}{3}=2\text{ (cm)}.$

Suy ra $a=\frac{2\cdot 3}{\sqrt{3}}=2\sqrt{3}\text{ (cm).}$

Vậy $AB=2\sqrt{3}\text{ cm}.$

II. Đường tròn nội tiếp tam giác

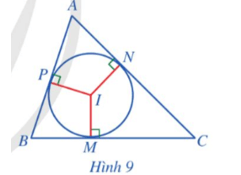
Hoạt động 5 trang 71 Toán 9 Tập 2: Cho tam giác ABC và đường tròn (I) (Hình 9). Nêu vị trí tương đối của các đường thẳng AB, BC, CA với đường tròn (I).

Lời giải:

Ta có AB ⊥ IP tại P thuộc đường tròn (I) nên AB là tiếp tuyến của đường tròn (I) hay AB tiếp xúc với đường tròn (I) tại P.

Tương tự, ta cũng có BC, CA tiếp xúc với đường tròn (I) lần lượt tại M, N.

Vậy các đường thẳng AB, BC, CA tiếp xúc với đường tròn (I) lần lượt tại P, M, N.

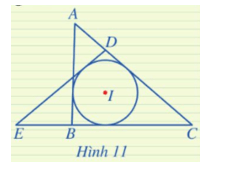
Luyện tập 4 trang 72 Toán 9 Tập 2: Trong Hình 11, đường tròn (I) là đường tròn nội tiếp những tam giác nào?

Lời giải:

Đường tròn (I) là đường tròn nội tiếp ∆ABC vì nó tiếp xúc với ba cạnh AB, BC, CA của tam giác.

Đường tròn (I) cũng là đường tròn nội tiếp ∆CDE vì nó tiếp xúc với ba cạnh CD, DE, EC của tam giác.

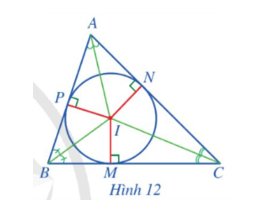
Hoạt động 6 trang 72 Toán 9 Tập 2: Cho tam giác ABC có I là giao điểm của ba đường phân giác. Gọi M, N, P lần lượt là hình chiếu của I trên các cạnh BC, CA, AB (Hình 12).

a) So sánh các đoạn thẳng IM, IN và IP.

b) Đặt r = IM. Đường tròn (I; r) có phải là đường tròn nội tiếp tam giác ABC hay không? Vì sao?

Lời giải:

a) Vì O là giao điểm của ba đường phân giác của tam giác ABC nên điểm O cách đều ba cạnh AB, BC, CA của tam giác ABC.

Do đó IP = IM = IN.

b) Ta có IM = IN = IP = r nên ba điểm M, N, P cùng nằm trên đường tròn (O; r).

Lại có IM ⊥ BC, IN ⊥ AC, IP ⊥ AB nên đường tròn (O; r) tiếp xúc với ba cạnh BC, AC, AB.

Vậy đường tròn (O; r) là đường tròn nội tiếp tam giác ABC.

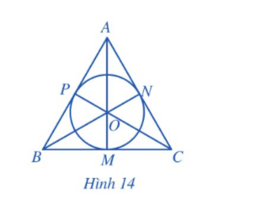
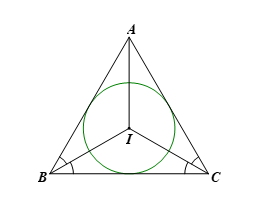
Hoạt động 7 trang 73 Toán 9 Tập 2: Cho tam giác đều ABC cạnh a, ba đường trung tuyến AM, BN, CP cắt nhau tại trọng tâm O (Hình 14).

a) AM, BN, CP có là các đường phân giác của tam giác ABC hay không?

b) Điểm O có là tâm đường tròn nội tiếp tam giác ABC hay không?

c) Tính OM theo a.

Lời giải:

a) Vì ∆ABC đều nên ba đường trung tuyến AM, BN, CP cũng đồng thời là các đường phân giác của tam giác ABC.

b) Vì ba đường phân giác AM, BN, CP của tam giác ABC cắt nhau tại điểm O nên O là tâm đường tròn nội tiếp tam giác ABC.

c) Vì ∆ABC đều nên $\widehat{ABM}=\widehat{ABC}=60°.$

Xét ∆ABM vuông tại M, ta có:

$AM=AB\cdot sin\widehat{ABM}=a\cdot \sin 60°=\frac{a\sqrt{3}}{2}.$

Tam giác ABC có AM là đường trung tuyến và O là trọng tâm của tam giác.

Do đó $OM=\frac{1}{3}AM=\frac{1}{3}\cdot \frac{a\sqrt{3}}{2}=\frac{a\sqrt{3}}{6}.$

Vậy $OM=\frac{a\sqrt{3}}{6}.$

Luyện tập 5 trang 73 Toán 9 Tập 2: Cho tam giác đều ABC ngoại tiếp đường tròn (O; 6 cm). Tính AB.

Lời giải:

Gọi độ dài các cạnh của tam giác đều ABC là a (cm). Khi đó AB = a (cm).

Vì tam giác ABC đều ngoại tiếp đường tròn (O; 6 cm) nên ta có $6=\frac{a\sqrt{3}}{6}\text{ (cm).}$

Suy ra $a=\frac{6\cdot 6}{\sqrt{3}}=12\sqrt{3}\text{ (cm).}$

Vậy $AB=12\sqrt{3}\text{ cm}.$

Bài tập

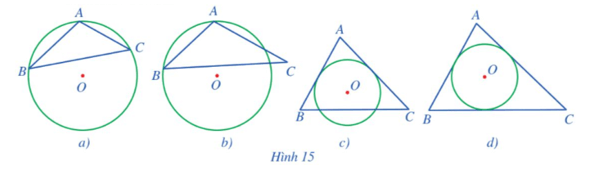
Bài 1 trang 73 Toán 9 Tập 2: Trong các hình 15a, 15b, 15c, 15d, ở hình nào ta có đường tròn (O) là đường tròn ngoại tiếp tam giác ABC? Ở hình nào ta có đường tròn (O) là đường tròn nội tiếp tam giác ABC? Vì sao?

Lời giải:

⦁ Ở Hình 15a, đường tròn (O) là đường tròn ngoại tiếp tam giác ABC, vì đường tròn (O) đi qua cả ba đỉnh A, B, C của tam giác ABC.

⦁ Ở Hình 15b, đường tròn (O) không là đường tròn ngoại tiếp tam giác ABC vì nó không đi qua đỉnh C của tam giác ABC.

⦁ Ở Hình 15c, đường tròn (O) không là đường tròn nội tiếp tam giác ABC, vì nó không tiếp xúc với cạnh BC.

⦁ Ở Hình 15d, đường tròn (O) là đường tròn nội tiếp tam giác ABC, vì nó tiếp xúc với ba cạnh AB, BC, CA của tam giác ABC.

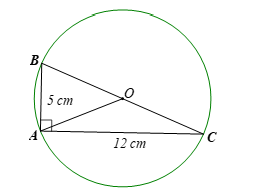
Bài 2 trang 74 Toán 9 Tập 2: Tính bán kính đường tròn ngoại tiếp tam giác ABC vuông tại A, biết AB = 5 cm, AC = 12 cm.

Lời giải:

Xét ∆ABC vuông tại A, theo định lí Pythagore, ta có:

BC² = AB² + AC² = 5² + 12² = 169.

Suy ra BC = 13 (cm).

Mặt khác, đường tròn ngoại tiếp tam giác vuông ABC có tâm là trung điểm O của cạnh huyền BC và bán kính bằng nửa cạnh huyền BC.

Vậy bán kính đường tròn ngoại tiếp tam giác ABC vuông tại A là $\frac{BC}{2}=\frac{13}{2}=6,5\text{ (cm).}$

Bài 3 trang 74 Toán 9 Tập 2: Cho bán kính đường tròn nội tiếp tam giác đều bằng 4 cm. Tính cạnh của tam giác đều đó.

Lời giải:

Giả sử đường tròn (I; 4 cm) nội tiếp tam giác đều ABC có cạnh bằng a (cm). Khi đó AB = a (cm).

Vì tam giác ABC đều ngoại tiếp đường tròn (I; 4 cm) nên ta có $4=\frac{a\sqrt{3}}{6}\text{ (cm).}$

Suy ra $a=\frac{4\cdot 6}{\sqrt{3}}=8\sqrt{3}\text{ (cm).}$

Vậy $AB=8\sqrt{3}\text{ cm}.$

Bài 4 trang 74 Toán 9 Tập 2: Một chiếc máy quay ở đài truyền hình được đặt trên giá đỡ ba chân, các điểm tiếp xúc với mặt đất của ba chân lần lượt là ba đỉnh A, B, C của tam giác đều ABC (Hình 10). Tính khoảng cách giữa hai vị trí A và B, biết bán kính đường tròn ngoại tiếp tam giác ABC là 4 dm.

Lời giải:

Giả sử tam giác ABC đều có cạnh bằng a (dm) nội tiếp đường tròn (O; 4 dm).

Khi đó AB = a (dm).

Vì tam giác đều ABC nội tiếp đường tròn (O) nên ta có $4=\frac{a\sqrt{3}}{3}\text{ (dm).}$

Suy ra $a=\frac{4\cdot 3}{\sqrt{3}}=4\sqrt{3}\text{ (dm).}$

Vậy $AB=4\sqrt{3}\text{ dm}.$

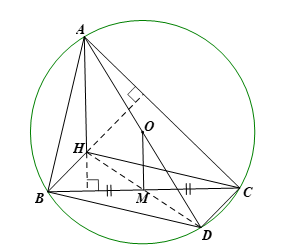
Bài 5 trang 74 Toán 9 Tập 2: Cho tam giác nhọn ABC (AB < AC) nội tiếp đường tròn (O) đường kính AD = 2R. Gọi M là trung điểm của cạnh BC và H là trực tâm của tam giác ABC. Chứng minh:

a) DB ⊥ AB và CD ⊥ AC;

b) Tứ giác BHCD là hình bình hành;

c) AC² + BH² = 4R²;

d) Ba điểm H, M, D thẳng hàng và AH = 2OM.

Lời giải:

a) Vì góc ABD, góc ACD đều là các góc nội tiếp chắn nửa đường tròn (O) (do AD là đường kính của (O)) nên $\widehat{ABD}=\widehat{ACD}=90°.$

Do đó DB ⊥ AB và CD ⊥ AC.

b) Vì H là trực tâm của ∆ABC nên BH ⊥ AC và CH ⊥ AB.

Lại có CD ⊥ AC và DB ⊥ AB (câu a) nên BH // CD và CH // BD.

Xét tứ giác BHCD có BH // CD và CH // BD nên BHCD là hình bình hành.

c) Vì BHCD là hình bình hành nên BH = CD.

Xét ∆ACD vuông tại C, theo định lí Pythagore, ta có:

AD² = AC² + CD²

Suy ra (2R)² = AC² + BH²

Hay AC² + BH² = 4R².

d) Vì BHCD là hình bình hành nên hai đường chéo BC và HD cắt nhau tại trung điểm của mỗi đường.

Mà M là trung điểm của BC nên M cũng là trung điểm của HD, do đó ba điểm H, M, D thẳng hàng.

Lại có AD là đường kính của đường tròn (O) nên O là trung điểm của AD.

Xét ∆AHD có O, M lần lượt là trung điểm của AB, HD nên OM là đường trung bình của tam giác,

Do đó $OM=\frac{1}{2}AH$ hay AH = 2OM.

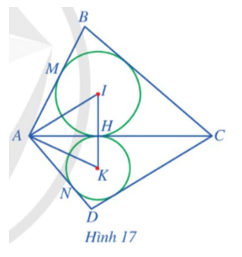
Bài 6 trang 74 Toán 9 Tập 2: Cho tứ giác ABCD có các tam giác ABC và ADC lần lượt ngoại tiếp các đường tròn (I) và (K) sao cho hai đường tròn này cùng tiếp xúc với đường thẳng AC tại điểm H thuộc đoạn thẳng AC. Giả sử đường tròn (I) tiếp xúc với cạnh AB tại M, đường tròn (K) tiếp xúc với cạnh AD tại N (Hình 17).

Chứng minh:

a) Ba điểm I, H, K thẳng hàng;

b) AM = AN;

c) $\widehat{IAK}=\frac{1}{2}\widehat{BAD}.$

Lời giải:

a) Vì đường tròn (I) tiếp xúc với đường thẳng AC tại điểm H nên IH ⊥ AC tại H, do đó $\widehat{IHA}=90°.$

Vì đường tròn (K) tiếp xúc với đường thẳng AC tại điểm H nên KH ⊥ AC tại H, do đó $\widehat{KHA}=90°.$

Ta có $\widehat{IHK}=\widehat{IHA}+\widehat{KHA}=90°+90°=180°.$

Suy ra ba điểm I, H, K thẳng hàng.

b) Xét đường tròn (I) có hai tiếp tuyến AB, AC cắt nhau tại A nên điểm A cách đều hai tiếp điểm M và H hay AM = AH (tính chất hai tiếp tuyến cắt nhau).

Xét đường tròn (K) có hai tiếp tuyến AD, AC cắt nhau tại A nên điểm A cách đều hai tiếp điểm N và H hay AN = AH (tính chất hai tiếp tuyến cắt nhau).

Do đó AM = AN.

c) Xét đường tròn (I) có hai tiếp tuyến AB, AC cắt nhau tại A nên AI là đường phân giác của góc BAC, do đó $\widehat{IAH}=\frac{1}{2}\widehat{BAC}.$

Xét đường tròn (K) có hai tiếp tuyến AD, AC cắt nhau tại A nên AK là đường phân giác của góc CAD, do đó $\widehat{HAK}=\frac{1}{2}\widehat{CAD}.$

Ta có: $\widehat{IAK}=\widehat{IAH}+\widehat{HAK}=\frac{1}{2}\widehat{BAC}+\frac{1}{2}\widehat{CAD}=\frac{1}{2}\left(\widehat{BAC}+\widehat{CAD}\right)=\frac{1}{2}\widehat{BAD}.$

Vậy $\widehat{IAK}=\frac{1}{2}\widehat{BAD}.$

Xem thêm Lời giải bài tập Toán 9 Cánh diều hay, chi tiết khác:

Bài 2: Tứ giác nội tiếp đường tròn

Bài tập cuối chương 8

Bài 1: Đa giác đều. Hình đa giác đều trong thực tiễn

Bài 2: Phép quay

Bài tập cuối chương 9