Giải Toán 9 Bài 1 (Cánh diều): Hàm số y = ax^2 (a ≠ 0)

Giải bài tập Toán 9 Bài 1: Hàm số y = ax^2 (a ≠ 0)

Khởi động trang 46 Toán 9 Tập 2: Galileo Galilei (1564 – 1642), sinh tại thành phố Pisa (Italia), là nhà bác học vĩ đại của thời kì Phục Hưng. Ông được mệnh danh là “cha đẻ của khoa học hiện đại”. Ngày 24/01/1590, tại đỉnh tháp nghiêng Pisa, ông đã thả hai quả cầu bằng chì có trọng lượng khác nhau để làm thí nghiệm nghiên cứu chuyển động của vật rơi tự do. Ông khẳng định rằng khi một vật rơi tự do (nếu không kể đến sức cản của không khí), tốc độ của vật rơi tăng dần và không phụ thuộc vào trọng lượng của vật. Quãng đường chuyển động y (m) của một vật rơi tự do được biểu diễn gần đúng bởi công thức y = 5x² với x là thời gian tính bằng giây.

Hàm số y = 5x² và đồ thị của hàm số đó có những tính chất như thế nào?

Lời giải:

Sau bài học này, chúng ta sẽ trả lời được câu hỏi trên như sau:

Hàm số y = 5x² có dạng y = ax² (a ≠ 0).

Đồ thị của hàm số y = 5x² là một parabol đi qua gốc tọa độ và nhận trục Oy làm trục đối xứng.

Đặc biệt, hàm số y = 5x² có hệ số a = 5 > 0 nên đồ thị của nó nằm phía trên trục hoành.

I. Hàm số y = ax² (a ≠ 0)

Hoạt động 1 trang 46 Toán 9 Tập 2: Xét hàm số y = 5x² trong tình huống ở phần mở đầu.

Hàm số đó có dạng y = ax² (a ≠ 0) hay không? Nếu có, hãy xác định hệ số a của x².

Lời giải:

Hàm số y = 5x² có dạng y = ax² (a ≠ 0) và có hệ số a = 5.

Luyện tập 1 trang 47 Toán 9 Tập 2: Hàm số nào sau đây có dạng y = ax² (a ≠ 0)? Đối với những hàm số đó, xác định hệ số a của x².

a) y = –x².

b) $y=\frac{x^2}{2}.$

c) $y=\frac{1}{4x^2}.$

Lời giải:

Các hàm số có dạng y = ax² (a ≠ 0) là:

a) y = –x², có a = –1;

b) $y=\frac{x^2}{2},$ có $a=\frac{1}{2}.$

Luyện tập 2 trang 47 Toán 9 Tập 2: Cho hàm số $y=\frac{2}{3}{x}^2.$ Tính giá trị của y khi:

a) x = –3;

b) x = 0;

c) x = 3.

Lời giải:

a) Với x = –3 thì $y=\frac{2}{3}\cdot {\left(-3\right)}^2=\frac{2}{3}\cdot 9=6.$

b) Với x = 0 thì $y=\frac{2}{3}\cdot 0^2=0.$

c) Với x = 3 thì $y=\frac{2}{3}\cdot 3^2=\frac{2}{3}\cdot 9=6.$

II.Đồ thị hàm số y = ax² (a ≠ 0)

Hoạt động 2 trang 47 Toán 9 Tập 2: a) Nêu khái niệm đồ thị của hàm số y = f(x).

b) Xét hàm số y = 2x². Hãy thực hiện các hoạt động sau:

– Tìm giá trị của y tương ứng với giá trị của x trong bảng sau:

– Trong mặt phẳng tọa độ Oxy, xác định các điểm có hoành độ và tung độ như trong bảng giá trị trên.

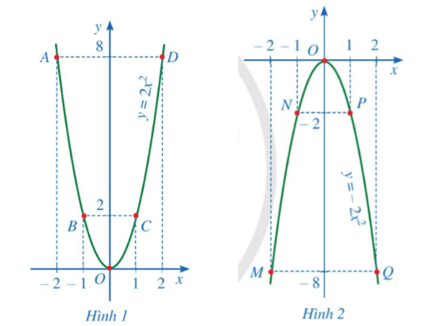
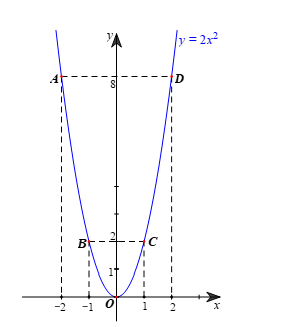
– Quan sát Hình 1, vẽ đường cong như ở Hình 1 đi qua 5 điểm A, B, O, C, D. Đường cong đó được gọi là đường parabol và đường parabol đó là đồ thị hàm số y = 2x².

c) Xét hàm số y = –2x². Hãy thực hiện các hoạt động sau:

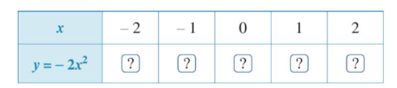
– Tìm giá trị của y tương ứng với giá trị của x trong bảng sau:

– Trong mặt phẳng tọa độ Oxy, xác định các điểm có hoành độ và tung độ như trong bảng giá trị trên.

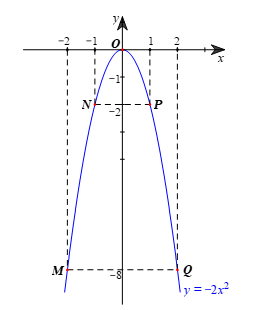
– Quan sát Hình 2, vẽ đường cong như ở Hình 2 đi qua 5 điểm M, N, O, P, Q. Đường cong đó được gọi là đường parabol và đường parabol đó là đồ thị hàm số y = –2x².

Lời giải:

a) Đồ thị của hàm số y = f(x) là tập hợp tất cả các điểm biểu diễn các cặp giá trị tương ứng (x; f(x)) trên mặt phẳng tọa độ.

b) Xét hàm số y = 2x².

Với x = –2 thì y = 2.(–2)² = 8;

Với x = –1 thì y = 2.(–1)² = 2;

Với x = 0 thì y = 2.0² = 0;

Với x = 1 thì y = 2.1² = 2;

Với x = 2 thì y = 2.2² = 8.

Ta có bảng sau:

Biểu diễn các điểm A(–2; 8); B(–1; 2); O(0; 0); C(1; 2); D(2; 8) trên mặt phẳng tọa độ Oxy và vẽ đường cong đi qua 5 điểm đó như ở Hình 1, ta được hình vẽ sau:

c) Thay lần lượt các giá trị x = –2; x = –1; x = 0; x = 1; x = 2 vào hàm số y = –2x² (tương tự câu b), ta được bảng sau:

Biểu diễn các điểm M(–2; –8); N(–1; –2); O(0; 0); P(1; –2); Q(2; –8) trên mặt phẳng tọa độ Oxy và vẽ đường cong đi qua 5 điểm đó như ở Hình 2, ta được hình vẽ sau:

Luyện tập 3 trang 49 Toán 9 Tập 2: Vẽ đồ thị của hàm số y = –3x².

Lời giải:

– Ta có bảng giá trị của y tương ứng với giá trị của x như sau:

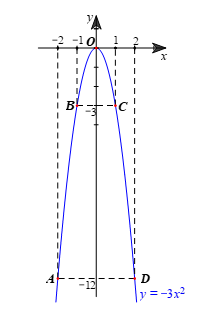
– Vẽ các điểm A(–2; –12); B(–1; –3); O(0; 0); C(1; –3); D(2; –12) thuộc đồ thị hàm số y = –3x² trong mặt phẳng tọa độ Oxy.

– Vẽ đường parabol đi qua 5 điểm A, B, O, C, D, ta nhận được đồ thị của hàm số y = –3x² (hình vẽ).

Hoạt động 3 trang 49 Toán 9 Tập 2: Quan sát đồ thị của hàm số $y=\frac{1}{2}{x}^2$ ở Hình 4, hãy nêu nhận xét về vị trí cặp điểm E và H; F và G đối với trục Oy.

Lời giải:

⦁ Cặp điểm E(–2; 2) và H(2; 2) có hoành độ đối nhau và tung độ bằng nhau. Hai điểm E và H đối xứng với nhau qua trục Oy.

⦁ Cặp điểm $F\left(-1;\frac{1}{2}\right)$ và $G\left(1;\frac{1}{2}\right)$ có hoành độ đối nhau và tung độ bằng nhau. Hai điểm F và G đối xứng với nhau qua trục Oy.

Bài tập

Bài 1 trang 51 Toán 9 Tập 2: Cho hàm số y = ax². Tìm a, biết rằng khi x = –3 thì y = 5.

Lời giải:

Với x = –3 và y = –5 thay vào hàm số y = ax², ta có:

–5 = a.(–3)² hay –5 = 9a, suy ra $a=-\frac{5}{9}.$

Vậy $a=-\frac{5}{9}$ khi khi x = –3 thì y = 5.

Bài 2 trang 51 Toán 9 Tập 2: Cho hàm số $y=\frac{1}{3}{x}^2.$

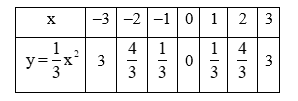
a) Tìm giá trị của y tương ứng với giá trị của x trong bảng sau:

b) Dựa vào bảng giá trị trên, vẽ đồ thị của hàm số đó.

c) Tìm những điểm thuộc đồ thị của hàm số có hoành độ lần lượt bằng –6; 10.

d) Tìm những điểm thuộc đồ thị của hàm số có tung độ bằng 27.

Lời giải:

a) Xét hàm số $y=\frac{1}{3}{x}^2:$

⦁ Với x = –3 thì $y=\frac{1}{3}\cdot {\left(-3\right)}^2=3.$

⦁ Với x = –2 thì $y=\frac{1}{3}\cdot {\left(-2\right)}^2=\frac{4}{3}.$

⦁ Với x = –1 thì $y=\frac{1}{3}\cdot {\left(-1\right)}^2=\frac{1}{3}.$

⦁ Với x = 0 thì $y=\frac{1}{3}\cdot 0^2=0.$

⦁ Với x = 1 thì $y=\frac{1}{3}\cdot 1^2=\frac{1}{3}.$

⦁ Với x = 2 thì $y=\frac{1}{3}\cdot 2^2=\frac{4}{3}.$

⦁ Với x = 3 thì $y=\frac{1}{3}\cdot 3^2=3.$

Ta có bảng sau:

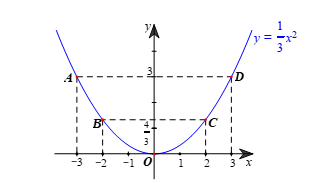
b) – Vẽ các điểm A(–3; 3); $B\left(–2;\frac{4}{3}\right);$ O(0; 0); $C\left(2;\frac{4}{3}\right);$ D(3; 3) thuộc đồ thị hàm số $y=\frac{1}{3}{x}^2$ trong mặt phẳng tọa độ Oxy.

– Vẽ đường parabol đi qua 5 điểm A, B, O, C, D, ta nhận được đồ thị của hàm số $y=\frac{1}{3}{x}^2$ (hình vẽ).

c) ⦁ Điểm có hoành độ bằng –6 tức là x = –6.

Với x = –6, thay vào hàm số $y=\frac{1}{3}{x}^2,$ ta được $y=\frac{1}{3}\cdot {\left(-6\right)}^2=12.$

Suy ra điểm thuộc đồ thị hàm số $y=\frac{1}{3}{x}^2$ có hoành độ bằng –6 thì có tọa độ (–6; 12).

⦁ Điểm có hoành độ bằng 10, tức là x = 10.

Với x = 10, thay vào hàm số $y=\frac{1}{3}{x}^2,$ ta được $y=\frac{1}{3}\cdot {10}^2=\frac{100}{3}.$

Suy ra điểm thuộc đồ thị hàm số $y=\frac{1}{3}{x}^2$ có hoành độ bằng 10 thì có tọa độ $\left(10;\frac{100}{3}\right).$

d) Điểm có tung độ bằng 27, tức là y = 27.

Với y = 27, thay vào hàm số $y=\frac{1}{3}{x}^2,$ ta được:

81 = x², suy ra x = 9 hoặc x = –9.

Vậy những điểm thuộc đồ thị hàm số $y=\frac{1}{3}{x}^2$ có tung độ bằng 27 thì có tọa độ là (9; 27) và (–9; 27).

Bài 3 trang 51 Toán 9 Tập 2: Trong mặt phẳng toạ độ Oxy, điểm M(2; –1) thuộc đồ thị của hàm số y = ax²

a) Tìm hệ số a.

b) Điểm A(4; –4) có thuộc đồ thị của hàm số hay không?

c) Hãy tìm một số điểm (không kể điểm O) thuộc đồ thị của hàm số, rồi vẽ đồ thị của hàm số.

Lời giải:

a) Vì đồ thị hàm số đi qua điểm M(2; –1) nên x = 2, y = –1 thỏa mãn hàm số y = ax².

Thay x = 2, y = –1 vào hàm số y = ax², ta được:

–1 = a.2² hay 4a = –1, suy ra $a=-\frac{1}{4}.$

Vậy $a=-\frac{1}{4}.$

b) Với $a=-\frac{1}{4}$ ta có hàm số $y=-\frac{1}{4}{x}^2.$

Xét điểm A(4; –4): Do $-4=-\frac{1}{4}\cdot 4^2$ nên điểm A(4; –4) thuộc đồ thị hàm số $y=-\frac{1}{4}{x}^2.$

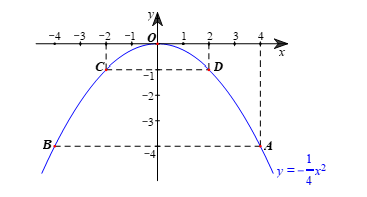
c) Xét hàm số $y=-\frac{1}{4}{x}^2.$

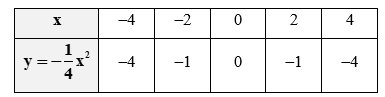
– Ta có bảng giá trị của y tương ứng với giá trị của x như sau:

– Vẽ các điểm B(–4; –4); C(–2; –1); O(0; 0); D(2; –1); A(4; –4) thuộc đồ thị hàm số $y=-\frac{1}{4}{x}^2$ trong mặt phẳng tọa độ Oxy.

– Vẽ đường parabol đi qua 5 điểm A, B, O, C, D, ta nhận được đồ thị của hàm số $y=-\frac{1}{4}{x}^2$ (hình vẽ).

Bài 4 trang 51 Toán 9 Tập 2: Hàm số y = at² biểu thị quãng đường (đơn vị: mét) mà một chiếc xe đua đi được trong khoảng thời gian t (giây). Giả sử một chiếc xe đua đi được 125 m sau khoảng thời gian là 5 giây.

a) Tìm hệ số a.

b) Vẽ đồ thị của hàm số đó.

Lời giải:

a) Vì chiếc xe đua đi được 125 m sau khoảng thời gian là 5 giây nên ta có: y = 125 và t = 5.

Thay y = 125 và t = 5 vào hàm số y = at², ta có:

125 = a.5² hay 25a = 125. Suy ra a = 5.

Vậy a = 5.

b) Với a = 5 ta có hàm số sau: y = 5t².

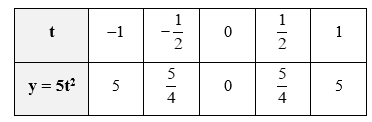
– Ta có bảng giá trị của y tương ứng với giá trị của t như sau:

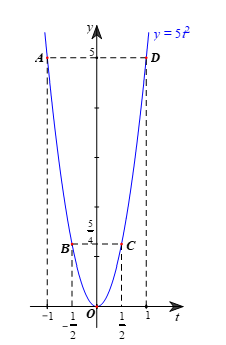
– Vẽ các điểm A(–1; 5); $B\left(-\frac{1}{2};\frac{5}{4}\right);$ O(0; 0); $C\left(\frac{1}{2};\frac{5}{4}\right);$ D(1; 5) thuộc đồ thị hàm số y = 5t² trong mặt phẳng tọa độ Oty.

– Vẽ đường parabol đi qua 5 điểm A, B, O, C, D, ta nhận được đồ thị của hàm số y = 5t² (hình vẽ).

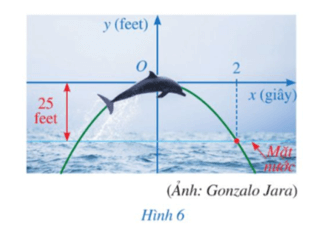
Bài 5 trang 51 Toán 9 Tập 2: Cá heo có thể nhảy cao tới 25 feet và thực hiện các thủ thuật như nhảy qua vòng, lộn nhào trong không trung. Giả sử quỹ đạo nhảy của cá heo là parabol y = ax², với gốc tọa độ là vị trí cao nhất mà cá heo đạt được, cách mặt nước 25 feet, trong đó y được tính theo đơn vị feet và x được tính theo đơn vị giây (Hình 6). Biết rằng sau 2 giây kể từ vị trí cao nhất đó, cá heo rơi chạm mặt nước. Tìm hàm số biểu thị quỹ đạo nhảy của cá heo.

Lời giải:

Vì quỹ đạo nhảy của cá heo là parabol y = ax², với gốc tọa độ là vị trí cao nhất mà cá heo đạt được nên đồ thị của hàm số y = ax² nằm bên dưới trục hoành.

Mà theo bài, sau 2 giây kể từ vị trí cao nhất cách mặt nước 25 feet, cá heo rơi chạm mặt nước nên ta có x = 2 và y = –25.

Thay x = 2 và y = –25 vào hàm số y = ax², ta được:

–25 = a.2² hay 4a = –25. Suy ra $a=–\frac{25}{4}.$

Vậy hàm số biểu thị quỹ đạo nhảy của cá heo là $y=-\frac{25}{4}{x}^2.$

Xem thêm Lời giải bài tập Toán 9 Cánh diều hay, chi tiết khác:

Bài 2: Phương trình bậc hai một ẩn

Bài 3: Định lí Viète

Bài tập cuối chương 7

Chủ đề 2: Mật độ dân số

Bài 1: Đường tròn ngoại tiếp tam giác. Đường tròn nội tiếp tam giác