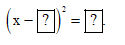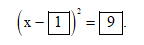Giải Toán 9 Bài 2 (Cánh diều): Phương trình bậc hai một ẩn

Giải bài tập Toán 9 Bài 2: Phương trình bậc hai một ẩn

Khởi động trang 52 Toán 9 Tập 2: Giả sử khi ném một quả bóng vào rổ, độ cao y (feet) của quả bóng và thời gian x (giây) liên hệ với nhau bởi công thức:

y = –5,8x² + 11,8x + 7.

(Nguồn: https://askiitians.com)

Khi quả bóng chạm đất, ta có thời gian x thoả mãn phương trình:

–5,8x² + 11,8x + 7 = 0.

Làm thế nào để giải đuợc phuơng trình trên?

Lời giải:

Sau bài học này, chúng ta sẽ giải quyết được câu hỏi trên như sau:

Giải phương trình: –5,8x² + 11,8x + 7 = 0 với x > 0.

Phương trình có các hệ số a = –5,8; b = 11,8, c = 7,

∆ = 11,8² – 4.(–5,8).7 = 301,64 > 0.

Do ∆ > 0 nên phương trình trên có hai nghiệm phân biệt là:

$x_1=\frac{-11,8+\sqrt{301,64}}{2\cdot \left(-5,8\right)}\approx -0,5$ (không thỏa mãn điều kiện x > 0);

$x_2=\frac{-11,8-\sqrt{301,64}}{2\cdot \left(-5,8\right)}\approx 2,5$ (thỏa mãn điều kiện x > 0).

Vậy sau khoảng 2,5 giây ném bóng thì quả bóng chạm đất.

I. Định nghĩa

Hoạt động 1 trang 52 Toán 9 Tập 2: Trong bài toán ở phần mở đầu, đối với đa thức –5,8x² + 11,8x + 7 ở vế trái của phương trình, hãy xác định: bậc; hệ số của x², hệ số của x và hệ số tự do.

Lời giải:

Đa thức –5,8x² + 11,8x + 7 ở vế trái của phương trình có bậc là 2; hệ số của x² là –5,8; hệ số của x là 11,8 và hệ số tự do là 7.

Luyện tập 1 trang 52 Toán 9 Tập 2: Cho hai ví dụ về:

a) Phương trình bậc hai ẩn t;

b) Phương trình không phải là phương trình bậc hai một ẩn.

Lời giải:

a) Hai ví dụ về phương trình bậc hai ẩn t:

t² – 2t + 3 = 0; t² + 1 = 0.

b) Hai ví dụ về phương trình không phải là phương trình bậc hai một ẩn:

0x² – x = 2; x + 1 = 0.

II. Giải phương trình

Hoạt động 2 trang 53 Toán 9 Tập 2: Giải các phương trình:

a) (x – 2)² = 0;

b) (x – 1)² = 9;

c) (x – 3)² = –1.

Lời giải:

a) (x – 2)² = 0

x – 2 = 0

x = 2.

Vậy phương trình đã cho có một nghiệm là x = 2.

b) (x – 1)² = 9

x – 1 = 3 hoặc x – 1 = –3

x = 4 hoặc x = –2.

Vậy phương trình đã cho có hai nghiệm là x = 4 và x = –2.

c) (x – 3)² = –1.

Vì (x – 3)² ≥ 0 với mọi x nên phương trình (x – 3)² = –1 vô nghiệm.

Luyện tập 2 trang 53 Toán 9 Tập 2: Giải phương trình: (x – 4)² = 11.

Lời giải:

Ta có:

(x – 4)² = 11

$x-4=\sqrt{11}$ hoặc $x-4=-\sqrt{11}$

$x=4+\sqrt{11}$ hoặc $x=4-\sqrt{11}.$

Vậy phương trình đã cho có hai nghiệm là $x=4+\sqrt{11}$ và $x=4-\sqrt{11}.$

Hoạt động 3 trang 53 Toán 9 Tập 2: Xét phương trình

2x² – 4x – 16 = 0 (1)

Chia hai vế của phương trình (1) cho 2, ta được phương trình:

x² – 2x – 8 = 0 (2)

a) Tìm số thích hợp cho khi biến đổi phương trình (2) về dạng:

b) Từ đó, hãy giải phương trình (2).

c) Nêu các nghiệm của phương trình (1).

Lời giải:

a) Ta có:

x² – 2x – 8 = 0

x² – 2x + 1 – 9 = 0

(x – 1)² = 9.

Vậy ta điền được số thích hợp cho như sau:

b) Ta có:

(x – 1)² = 9

x – 1 = 3 hoặc x – 1 = –3

x = 4 hoặc x = –2.

Vậy phương trình (2) có hai nghiệm là x = 4 và x = –2.

c) Vì chia hai vế của phương trình (1) cho số 2 khác 0, ta được phương trình (2) nên nghiệm của phương trình (2) chính là nghiệm của phương trình (1).

Vậy phương trình (1) có hai nghiệm là x = 4 và x = –2.

Luyện tập 3 trang 55 Toán 9 Tập 2: Giải các phương trình:

a) 3x² – x – 0,5 = 0;

b) 4x² + 10x + 15 = 0;

c) $-x^2+x-\frac{1}{4}=0.$

Lời giải:

a) 3x² – x – 0,5 = 0

Phương trình có các hệ số a = 3, b = –1, c = –0,5,

∆ = (–1)² – 4.3.(–0,5) = 7 > 0.

Do ∆ > 0 nên phương trình đã cho có 2 nghiệm phân biệt là:

$x_1=\frac{-\left(-1\right)+\sqrt{7}}{2\cdot 3}=\frac{1+\sqrt{7}}{6};$$x_2=\frac{-\left(-1\right)-\sqrt{7}}{2\cdot 3}=\frac{1-\sqrt{7}}{6}.$

b) 4x² + 10x + 15 = 0

Phương trình có các hệ số a = 4, b = 10, c = 15,

∆ = 10² – 4.4.15 = –140 < 0.

Do ∆ < 0 nên phương trình đã cho vô nghiệm.

c) $-x^2+x-\frac{1}{4}=0.$

Phương trình có các hệ số a = –1, b = 1, $c=-\frac{1}{4},$

$\Delta =1^2-4\cdot \left(-1\right)\cdot \left(\frac{-1}{4}\right)=0.$

Do ∆ = 0 nên phương trình đã cho có nghiệm kép $x_1=x_2=\frac{-1}{2\cdot \left(-1\right)}=\frac{1}{2}.$

Hoạt động 4 trang 55 Toán 9 Tập 2: Xét phương trình ax² + bx + c = 0 (a ≠ 0) với b = 2b’.

a) Đặt ∆’ = b’² – ac. Chứng tỏ rằng ∆ = 4∆’.

b) Xét tính có nghiệm và nêu công thức nghiệm (nếu có) của phương trình trong các trường hợp: ∆’ > 0; ∆’ = 0; ∆’ < 0.

Lời giải:

a) Ta có ∆ = b² – 4ac = (2b’)² – 4ac = 4b’² – 4ac = 4(b’² – ac) = 4∆’.

Vậy ∆ = 4∆’.

b) Trường hợp 1: ∆’ > 0 nên 4∆’ > 0 hay ∆ > 0.

Khi đó phương trình có hai nghiệm phân biệt là:

$x_1=\frac{-b+\sqrt{\Delta }}{2a}=\frac{-2b^{\text{'}}+\sqrt{4{\Delta }^{\text{'}}}}{2a}=\frac{-2b^{\text{'}}+2\sqrt{{\Delta }^{\text{'}}}}{2a}=\frac{-b^{\text{'}}+\sqrt{{\Delta }^{\text{'}}}}{a};$

$x_1=\frac{-b-\sqrt{\Delta }}{2a}=\frac{-2b^{\text{'}}-\sqrt{4{\Delta }^{\text{'}}}}{2a}=\frac{-2b^{\text{'}}-2\sqrt{{\Delta }^{\text{'}}}}{2a}=\frac{-b^{\text{'}}-\sqrt{{\Delta }^{\text{'}}}}{a}.$

Trường hợp 2: ∆’ = 0 nên 4∆’ = 0 hay ∆ = 0.

Khi đó phương trình có nghiệm kép là:

$x_1=x_2=\frac{-b}{2a}=\frac{-2b^{\text{'}}}{2a}=\frac{-b^{\text{'}}}{a}.$

Trường hợp 3: ∆’ < 0 nên 4∆’ < 0 hay ∆ < 0.

Khi đó phương trình vô nghiệm.

Luyện tập 4 trang 56 Toán 9 Tập 2: Giải các phương trình:

a) x² – 6x – 5 = 0;

b) –3x² + 12x – 35 = 0;

c) –25x² + 30x – 9 = 0.

Lời giải:

a) x² – 6x – 5 = 0

Phương trình có các hệ số a = 1, b = –6, c = –5. Do b = –6 nên b’ = –3.

Ta có: ∆’ = (–3)² – 1.(–5) = 14 > 0.

Do ∆’ > 0 nên phương trình đã cho có hai nghiệm phân biệt là:

$x_1=\frac{-\left(-3\right)+\sqrt{14}}{1}=3+\sqrt{14};$$x_2=\frac{-\left(-3\right)-\sqrt{14}}{1}=3-\sqrt{14}.$

b) –3x² + 12x – 35 = 0

Phương trình có các hệ số a = –3, b = 12, c = –35. Do b = 12 nên b’ = 6.

Ta có: ∆’ = 6² – (–3).(–35) = –69 < 0.

Do ∆’ < 0 nên phương trình đã cho vô nghiệm.

c) –25x² + 30x – 9 = 0

Phương trình có các hệ số a = –25, b = 30, c = –9. Do b = 30 nên b’ = 15.

Ta có: ∆’ = 15² – (–25).(–9) = 0.

Do ∆’ = 0 nên phương trình đã cho có nghiệm kép $x_1=x_2=\frac{-15}{-25}=\frac{3}{5}.$

III. Ứng dụng của phương trình bậc hai một ẩn

Luyện tập 5 trang 58 Toán 9 Tập 2: Trong bài toán ở phần mở đầu, sau bao lâu thì quả bóng chạm đất?

Lời giải:

Giải phương trình: –5,8x² + 11,8x + 7 = 0 với x > 0.

Phương trình có các hệ số a = –5,8; b = 11,8, c = 7,

∆ = 11,8² – 4.(–5,8).7 = 301,64 > 0.

Do ∆ > 0 nên phương trình trên có hai nghiệm phân biệt là:

$x_1=\frac{-11,8+\sqrt{301,64}}{2\cdot \left(-5,8\right)}\approx -0,5$ (không thỏa mãn điều kiện x > 0);

$x_2=\frac{-11,8-\sqrt{301,64}}{2\cdot \left(-5,8\right)}\approx 2,5$ (thỏa mãn điều kiện x > 0).

Vậy sau khoảng 2,5 giây ném bóng thì quả bóng chạm đất.

IV.Sử dụng máy tính cầm tay để tìm nghiệm của phương trình bậc hai một ẩn

Luyện tập 6 trang 59 Toán 9 Tập 2: Sử dụng máy tính cầm tay tìm nghiệm của phương trình bậc hai một ẩn (làm tròn kết quả đến hàng phần mười):

$\sqrt{2}{x}^2-4x-\sqrt{3}=0.$

Lời giải:

Sử dụng loại máy tính phù hợp, ấn liên tiếp các phím:

Ta thấy trên màn hình hiện ra (kết quả gần đúng) x­₁ = 3,209971027.

Ấn tiếp phím ta thấy trên màn hình hiện ra (kết quả gần đúng) x₂ = –0,3815439022.

Vậy nghiệm của phương trình đã cho là x₁ ≈ 3,2; x₂ ≈ –0,4.

Bài tập

Bài 1 trang 59 Toán 9 Tập 2: Trong các phương trình sau, phương trình nào là phương trình bậc hai một ẩn? Đối với những phương trình bậc hai một ẩn đó, xác định hệ số a của x², hệ số b của x, hệ số tự do c.

a) $0,5x^2-5x+\sqrt{3}=0.$

b) 0x² – 0,25x + 6 = 0.

c) $-x^2+\sqrt{5}x=0.$

Lời giải:

a) Phương trình $0,5x^2-5x+\sqrt{3}=0$ là phương trình bậc hai ẩn x, có a = 0,5; b = –5; c = $\sqrt{3}.$

b) Phương trình 0x² – 0,25x + 6 = 0 không phải là phương trình bậc hai một ẩn vì a = 0.

c) Phương trình $-x^2+\sqrt{5}x=0$ là phương trình bậc hai ẩn x, có a = –1; b = $\sqrt{5};$ c = 0.

Bài 2 trang 59 Toán 9 Tập 2: Chứng minh rằng: Nếu ac < 0 thì phương trình ax² + bx + c (a ≠ 0) có hai nghiệm phân biệt. Điều ngược lại có đúng hay không? Vì sao?

Lời giải:

⦁ Xét phương trình ax² + bx + c (a ≠ 0) có ∆ = b² – 4ac.

Theo bài, nếu ac < 0 thì – 4ac > 0.

Mà b² ≥ 0 nên b² – 4ac > 0, hay ∆ > 0.

Khi đó, phương trình có hai nghiệm phân biệt.

⦁ Xét phương trình ax² + bx + c (a ≠ 0) có ∆ = b² – 4ac.

Nếu phương trình có hai nghiệm phân biệt thì ∆ > 0, hay b² – 4ac > 0, suy ra b² > 4ac.

Ta thấy có hai trường hợp xảy ra:

Trường hợp 1: b² > 4ac > 0 thì khi đó ta có ac > 0.

Trường hợp 2: 4ac < 0 thì khi đó ta có ac < 0.

Vậy khẳng định chiều ngược lại là không đúng.

Bài 3 trang 59 Toán 9 Tập 2: Giải các phương trình:

a) x² – x – 5 = 0;

b) 2x² – 0,5x + 0,03 = 0;

c) –16x² + 8x – 1 = 0;

d) –2x² + 5x – 4 = 0;

e) $\frac{1}{5}{x}^2-5=0;$

g) $3x^2-\sqrt{2}x=0.$

Lời giải:

a) x² – x – 5 = 0

Phương trình có các hệ số a = 1, b = –1, c = –5,

∆ = (–1)² – 4.1.(–5) = 21 > 0.

Do ∆ > 0 nên phương trình có hai nghiệm phân biệt là:

$x_1=\frac{-\left(-1\right)+\sqrt{21}}{2\cdot 1}=\frac{1+\sqrt{21}}{2};$$x_2=\frac{-\left(-1\right)-\sqrt{21}}{2\cdot 1}=\frac{1-\sqrt{21}}{2}.$

b) 2x² – 0,5x + 0,03 = 0

Phương trình có các hệ số a = 2; b = –0,5; c = 0,03;

∆ = (–0,5)² – 4.2.0,03 = 0,01 > 0.

Do ∆ > 0 nên phương trình có hai nghiệm phân biệt là:

$x_1=\frac{-\left(-0,5\right)+\sqrt{0,01}}{2\cdot 2}=\frac{0,5+0,1}{4}=\frac{0,6}{4}=0,15;$

$x_2=\frac{-\left(-0,5\right)-\sqrt{0,01}}{2\cdot 2}=\frac{0,5-0,1}{4}=\frac{0,4}{4}=0,1.$

c) –16x² + 8x – 1 = 0

Phương trình có các hệ số a = –16, b = 8, c = –1. Do b = 8 nên b’ = 4.

Ta có: ∆’ = 4² – (–16).(–1) = 0.

Do ∆’ = 0 nên phương trình có nghiệm kép $x_1=x_2=\frac{-4}{-16}=\frac{1}{4}.$

d) –2x² + 5x – 4 = 0

Phương trình có các hệ số a = –2, b = 5, c = –4,

∆ = 5² – 4.(–2).(–4) = –7 < 0.

Do ∆ < 0 nên phương trình đã cho vô nghiệm.

e) $\frac{1}{5}{x}^2-5=0$

Phương trình có các hệ số a = $\frac{1}{5},$ b = 0, c = –5. Do b = 0 nên b’ = 0.

Ta có: ${\Delta }^{\text{'}}=0^2-\frac{1}{5}\cdot \left(-5\right)=1>0.$

Do ∆’ > 0 nên phương trình có hai nghiệm phân biệt là:

$x_1=\frac{-0+\sqrt{1}}{\frac{1}{5}}=5;$$x_2=\frac{-0-\sqrt{1}}{\frac{1}{5}}=-5.$

g) $3x^2-\sqrt{2}x=0$

Phương trình có các hệ số a = 3, b = $-\sqrt{2},$ c = 0,

$\Delta ={\left(-\sqrt{2}\right)}^2-4\cdot 3\cdot 0=2>0.$

Do ∆ > 0 nên phương trình có hai nghiệm phân biệt là:

$x_1=\frac{-\left(-\sqrt{2}\right)+\sqrt{2}}{2\cdot 3}=\frac{2\sqrt{2}}{6}=\frac{\sqrt{2}}{3};$

$x_2=\frac{-\left(-\sqrt{2}\right)-\sqrt{2}}{2\cdot 3}=\frac{0}{6}=0.$

Bài 4 trang 60 Toán 9 Tập 2: Ra đa của một máy bay trực thăng theo dõi chuyển động của một ô tô trong 10 phút, phát hiện rằng tốc độ v (km/h) của ô tô thay đổi phụ thuộc vào thời gian t (phút) bởi công thức v = 3t² – 30t + 135. (Nguồn: Toán 9 – tập 2, NXB Giáo dục Việt Nam, 2020)

a) Tính tốc độ của ô tô khi t = 5.

b) Tính giá trị của t khi tốc độ ô tô bằng 120 km/h (theo đơn vị phút và làm tròn kết quả đến hàng đơn vị).

Lời giải:

a) Khi t = 5, thay vào công thức v = 3t² – 30t + 135, ta được:

v = 3.5² – 30.5 + 135 = 60.

Vậy khi t = 5 thì tốc độ của ô tô là 60 km/h.

b) Khi tốc độ của ô tô bằng 120 km/h, tức là v = 120, thay vào công thức v = 3t² – 30t + 135, ta có:

3t² – 30t + 135 = 120

3t² – 30t + 15 = 0

t² – 10t + 5 = 0.

Phương trình trên có các hệ số a = 1, b = –10, c = 5. Do b = –10 nên b’ = –5.

Ta có: ∆’ = (–5)² – 1.5 = 20 > 0.

Do ∆’ > 0 nên phương trình trên có hai nghiệm phân biệt là:

$t_1=\frac{-\left(-5\right)+\sqrt{20}}{1}=5+2\sqrt{5}\approx 9;$

$t_2=\frac{-\left(-5\right)-\sqrt{20}}{1}=5-2\sqrt{5}\approx 1.$

Ta thấy cả hai giá trị trên của t đều thỏa mãn điều kiện t > 0.

Vậy khi t ≈ 1 phút và t ≈ 9 phút thì tốc độ của ô tô bằng 120 km/h.

Bài 5 trang 60 Toán 9 Tập 2: Một nhà máy chuyên sản xuất một loại sản phẩm. Năm 2019, nhà máy sản xuất được 5 000 sản phẩm. Do ảnh hưởng của dịch bệnh nên sản lượng của nhà máy trong các năm 2020 và 2021 đều giảm, cụ thể: Số lượng sản phẩm thực tế sản xuất được của năm 2020 giảm x% so với số lượng sản phẩm sản xuất được của năm 2019; Số lượng sản phẩm thực tế sản xuất được của năm 2021 giảm x% so với số lượng sản phẩm thực tế sản xuất được của năm 2020. Biết rằng số lượng sản phẩm thực tế sản xuất được của năm 2021 giảm 51% so với số lượng sản phẩm sản xuất được của năm 2019. Tìm x.

Lời giải:

Do số lượng sản phẩm thực tế sản xuất được của năm 2020 giảm x% so với số lượng sản phẩm sản xuất được của năm 2019 nên số lượng sản phẩm sản xuất được năm 2020 là:

5 000 – 5 000.x% = 5 000 – 50x (sản phẩm).

Do số lượng sản phẩm thực tế sản xuất được của năm 2021 giảm x% so với số lượng sản phẩm thực tế sản xuất được của năm 2020 nên số lượng sản phẩm sản xuất được năm 2021 là:

5 000 – 50x – (5 000 – 50x).x%

= 5 000 – 50x – 50x + 0,5x²

= 5 000 – 100x + 0,5x² (sản phẩm).

Do số lượng sản phẩm thực tế sản xuất được của năm 2021 giảm 51% so với số lượng sản phẩm sản xuất được của năm 2019 nên số lượng sản phẩm sản xuất được năm 2021 là:

5 000 – 5 000.51% = 2 450.

Khi đó, ta có phương trình: 5 000 – 100x + 0,5x² = 2 450.

Giải phương trình:

5 000 – 100x + 0,5x² = 2 450

0,5x² – 100x + 2 550 = 0

x² – 200x + 5 100 = 0.

Phương trình trên có các hệ số a = 1, b = –200, c = 5 100. Do b = –200 nên b’ = –100.

Ta có: ∆’ = (–100)² – 1. 5 100 = 4 900 > 0.

Do ∆’ > 0 nên phương trình có hai nghiệm phân biệt là:

$x_1=\frac{-\left(-100\right)+\sqrt{4900}}{1}=100+70=170;$

$x_2=\frac{-\left(-100\right)-\sqrt{4900}}{1}=100-70=30.$

Ta thấy chỉ có giá trị x₂ = 30 thỏa mãn điều kiện vì x% < 100%.

Vậy x = 30 là giá trị cần tìm.

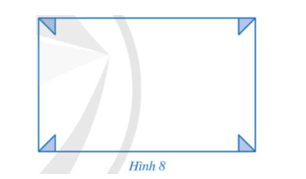
Bài 6 trang 60 Toán 9 Tập 2: Mảnh đất của bác An có dạng hình chữ nhật với chiều dài hơn chiều rộng 10 m. Ở mỗi góc của mảnh đất, bác An đã dành một phần đất có dạng tam giác vuông cân với cạnh góc vuông bằng $\frac{1}{8}$ chiều rộng của mảnh đất để trồng hoa (Hình 8). Tính chiều rộng mảnh đất đó, biết diện tích còn lại của mảnh đất không tính phần đất trồng hoa là 408 m².

Lời giải:

Gọi chiều rộng của mảnh đất là x (m) (x > 0).

Chiều dài của mảnh đất là x + 10 (m).

Diện tích mảnh đất hình chữ nhật là: x(x + 10) (m²).

Độ dài cạnh góc vuông của phần đất dạng tam giác vuông cân để trồng hoa là: $\frac{1}{8}$ (m).

Diện tích mảnh đất trồng hoa là: $\frac{1}{2}\cdot \frac{1}{8}x\cdot \frac{1}{8}x=\frac{1}{32}{x}^2$ (m²).

Diện tích phần đất còn lại là: $x\left(x+10\right)-\frac{1}{32}{x}^2$ (m²).

Theo bài, diện tích còn lại của mảnh đất không tính phần đất trồng hoa là 408 m² nên ta có phương trình: $x\left(x+10\right)-\frac{1}{32}{x}^2=408.$

Giải phương trình:

$x\left(x+10\right)-\frac{1}{32}{x}^2=408$

$x^2+10x-\frac{1}{32}{x}^2=408$

32x² + 320x – x² = 13 056

31x² + 320x – 13 056 = 0.

Phương trình trên có các hệ số a = 31, b = 320, c = –13 056.

Do b = 320 nên b’ = 160.

Ta có: ∆’ = 160² – 31.(–13 056) = 430 336 > 0.

Do ∆’ > 0 nên phương trình có hai nghiệm phân biệt là:

$x_1=\frac{-160+\sqrt{430336}}{31}=\frac{-160+656}{31}=16$(thỏa mãn điều kiện x > 0);

$x_2=\frac{-160-\sqrt{430336}}{31}=\frac{-160-656}{31}=-\frac{816}{31}$(không thỏa mãn điều kiện x > 0).

Vậy chiều rộng của mảnh đất đó là 16 m.

Xem thêm Lời giải bài tập Toán 9 Cánh diều hay, chi tiết khác:

Bài 3: Định lí Viète

Bài tập cuối chương 7

Chủ đề 2: Mật độ dân số

Bài 1: Đường tròn ngoại tiếp tam giác. Đường tròn nội tiếp tam giác

Bài 2: Tứ giác nội tiếp đường tròn