Giải Toán 9 Bài 1 (Cánh diều): Hình trụ

Giải bài tập Toán 9 Bài 1: Hình trụ

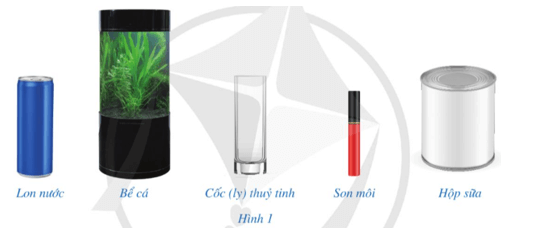
Khởi động trang 92 Toán 9 Tập 2: Ở tiểu học, ta đã nhận biết được một số đồ vật có dạng hình trụ như ở Hình 1.

Hình trụ có những đặc điểm gì?

Lời giải:

Sau bài học này, chúng ta sẽ trả lời được câu hỏi trên như sau:

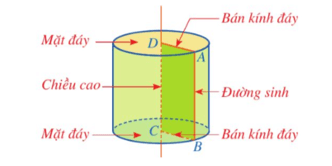
Hình trụ ở hình vẽ trên có:

⦁ Hình tròn tâm D bán kính DA và hình tròn tâm C bán kính CB là hai mặt đáy; hai mặt đáy của hình trụ bằng nhau và nằm trong hai mặt phẳng song song;

⦁ Độ dài cạnh DA được gọi là bán kính đáy;

⦁ Độ dài cạnh CD được gọi là chiều cao;

⦁ Cạnh AB quét nên mặt xung quanh của hình trụ, mỗi vị trí của cạnh AB được gọi là một đường sinh; độ dài đường sinh bằng chiều cao của hình trụ.

I. Hình trụ

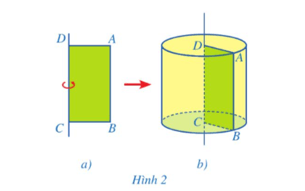
Hoạt động 1 trang 92 Toán 9 Tập 2: Cắt một miếng bìa có dạng hình chữ nhật ABCD. Khi quay miếng bìa một vòng quanh đường thẳng cố định chứa cạnh CD (Hình 2a), miếng bìa đó tạo nên một hình như ở Hình 2b. Hình đó có dạng hình gì?

Lời giải:

Hình được tạo ra khi quay hình chữ nhật ABCD một vòng xung quanh đường thẳng cố định chứa cạnh CD của nó là hình trụ.

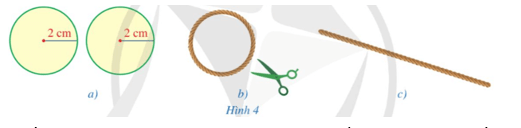
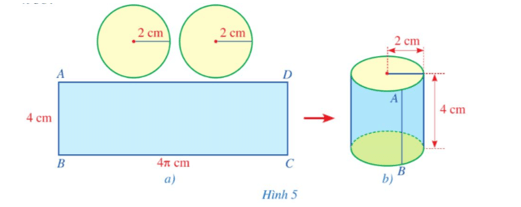
Hoạt động 2 trang 93 Toán 9 Tập 2: a) Cắt hai miếng bìa có dạng hình tròn với bán kính bằng 2 cm (Hình 4a).

b) Lấy một sợi dây dài mảnh không dãn và tạo vòng dây cuốn quanh (một vòng) miếng bìa tròn thứ nhất (Hình 4b), cắt vòng dây và kéo thẳng vòng dây đó để nhận được đoạn dây như ở Hình 4c.

Cắt một miếng bìa có dạng hình chữ nhật ABCD với chiều dài bằng độ dài đoạn dây ở Hình 4c và chiều rộng bằng 4 cm.

c) Ghép và dán các miếng bìa vừa cắt ở câu a, b (Hình 5a) để được một hình trụ như ở Hình 5b.

Lời giải:

HS thực hiện theo hướng dẫn của GV và SGK để cắt ghép được hình trụ.

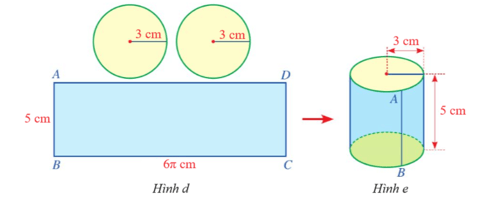
Luyện tập 1 trang 94 Toán 9 Tập 2: Tạo lập một hình trụ có bán kính đáy là 3 cm, chiều cao là 5 cm.

Lời giải:

Để tạo lập được một hình trụ có bán kính đáy là 3 cm, chiều cao là 5 cm, ta làm như sau:

Bước 1. Cắt hai miếng bìa có dạng hình tròn với bán kính bằng 3 cm (Hình a).

Bước 2. Lấy một sợi dây dài mảnh không dãn và tạo vòng dây cuốn quanh (một vòng) miếng bìa tròn thứ nhất (Hình b), cắt vòng dây và kéo thẳng vòng dây đó để nhận được đoạn dây như ở Hình c.

Bước 3. Cắt một miếng bìa có dạng hình chữ nhật ABCD với chiều dài bằng độ dài đoạn dây ở Hình c và chiều rộng bằng 5 cm.

Bước 4. Ghép và dán các miếng bìa vừa cắt ở Bước 1, Bước 3 (Hình d) để được một hình trụ như ở Hình e.

II. Diện tích xung quanh hình trụ

Hoạt động 3 trang 94 Toán 9 Tập 2: Thực hiện các hoạt động sau:

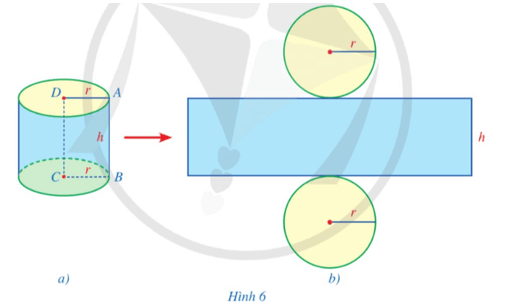
a) Chuẩn bị một hình trụ bằng giấy có bán kính đáy r và chiều cao h (Hình 6a);

b) Từ hình trụ đó, cắt rời hai đáy và cắt dọc theo đường sinh AB rồi trải phẳng ra, ta được hình khai triển mặt xung quanh của hình trụ là một hình chữ nhật (Hình 6b);

c) Hãy cho biết độ dài các cạnh của hình chữ nhật ở Hình 6b và tính diện tích của hình chữ nhật đó theo r và h.

Lời giải:

a) Chuẩn bị hình trụ bằng giấy có bán kính đáy r và chiều cao h như ở Hình 6a (tạo lập như Luyện tập 1, trang 94, SGK Toán lớp 9, Tập hai).

b) Cắt rời hai đáy và dùng thước thẳng kẻ đường sinh AB của hình trụ, cắt theo đường sinh AB rồi trải phẳng ra, ta được hình khai triển mặt xung quanh của hình trụ là một hình chữ nhật (Hình 6b).

c) Hình chữ nhật nhận được (Hình 6b) có chiều dài là chu vi đáy C của hình trụ và chiều rộng là chiều cao h của hình trụ.

Chu vi đáy của hình trụ là: C = 2πr.

Diện tích hình chữ nhật nhận được là:

S = C.h = 2πrh (đơn vị diện tích).

Luyện tập 2 trang 95 Toán 9 Tập 2: Bác An muốn sơn mặt xung quanh của một cây cột có dạng hình trụ với đường kính đáy là 30 cm và chiều cao là 350 cm. Chi phí để sơn cây cột đó là 40 000 đồng/1 m². Hỏi chi phí bác An cần bỏ ra để sơn mặt xung quanh của cây cột đó là bao nhiêu đồng (làm tròn kết quả đến hàng nghìn)?

Lời giải:

Bán kính đáy của cây cột có dạng hình trụ đó là:

R = 30 : 2 = 15 (cm).

Diện tích xung quanh của cây cột có dạng hình trụ đó là:

S = 2π.15.350 = 10 500π (cm²) = 1,05π (m²).

Chi phí bác An cần bỏ ra để sơn mặt xung quanh của cây cột đó là:

1,05π . 40 000 = 42 000π (đồng) ≈ 132 000 (đồng).

III. Thể tích hình trụ

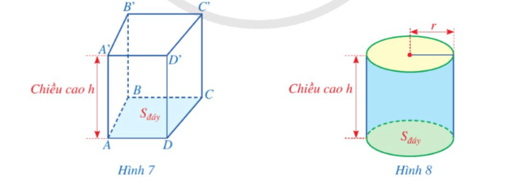
Hoạt động 4 trang 95 Toán 9 Tập 2: a) Nêu công thức tính thể tích hình lăng trụ đứng tứ giác ABCD.A’B’C’D’ (Hình 7) khi biết diện tích đáy và chiều cao.

b) Cũng như hình lăng trụ đứng tứ giác, mỗi hình trụ đều có thể tích. Hãy dự đoán cách tính thể tích của hình trụ (Hình 8).

Lời giải:

a) Công thức tính thể tích hình lăng trụ đứng tứ giác ABCD.A’B’C’D’ là:

V = S_đáy.h.

b) Dự đoán: Thể tích của hình trụ là V = S­_đáy.h = πr²h.

Bài tập

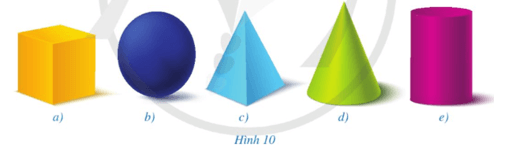
Bài 1 trang 96 Toán 9 Tập 2: Trong những vật thể ở các hình 10a, 10b, 10c, 10d, 10e, vật thể nào có dạng hình trụ?

Lời giải:

Trong những vật thể trên, vật thể có dạng hình trụ là Hình 10e.

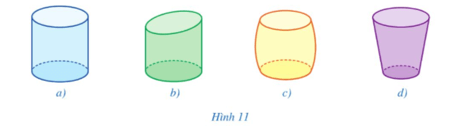
Bài 2 trang 96 Toán 9 Tập 2: Trong các hình 11a, 11b, 11c, 11d, hình nào có dạng hình trụ?

Lời giải:

Trong các hình trên, Hình 11a có dạng hình trụ.

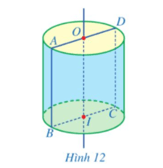
Bài 3 trang 97 Toán 9 Tập 2: Cho hình chữ nhật ABCD, các điểm O, I lần lượt là trung điểm các cạnh AD, BC. Xét hình trụ được tạo ra khi quay hình chữ nhật AOIB một vòng xung quanh đường thẳng cố định chứa cạnh OI của hình chữ nhật đó (Hình 12).

Quan sát Hình 12, hãy chỉ ra:

a) Bốn bán kính đáy của hình trụ;

b) Chiều cao của hình trụ;

c) Hai đường sinh của hình trụ.

Lời giải:

a) Bốn bán kính đáy của hình trụ là OA, OD, IB, IC.

b) Chiều cao của hình trụ là OI.

c) Hai đường sinh của hình trụ là AB và DC.

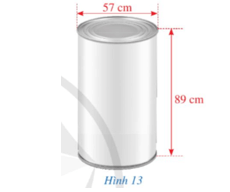
Bài 4 trang 97 Toán 9 Tập 2: Một doanh nghiệp sản xuất vỏ hộp bằng tôn có dạng hình trụ với hai đáy (Hình 13).

Hình trụ đó có đường kính đáy khoảng 57 cm và chiều cao khoảng 89 cm. Chi phí để sản xuất vỏ hộp đó là 100 000 đồng/m². Hỏi số tiền mà doanh nghiệp cần chi để sản xuất 1 000 vỏ hộp đó là bao nhiêu đồng (làm tròn kết quả đến hàng nghìn)?

Lời giải:

Bán kính đáy của hình trụ là:

$r=\frac{57}{2}=28,5\text{ (cm).}$

Diện tích toàn phần của vỏ hộp có dạng hình trụ là:

S_xq = 2πr(h + r) = 2π.28,5.(89 + 28,5) = 6 697,5π (cm²) = 0,66975π (m²).

Số tiền mà doanh nghiệp cần cho trả để sản xuất 1 000 vỏ hộp đó là:

0,66975π . 100 000 . 1 000 = 66 975 000π (đồng) ≈ 210 408 000 (đồng).

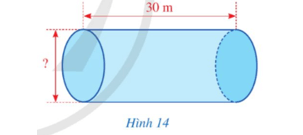
Bài 5 trang 97 Toán 9 Tập 2: Một đường ống nối hai bể cá trong một thuỷ cung có dạng hình trụ (không có hai đáy), với độ dài (hay chiều cao) là 30 m và có dung tích là 1 800 000 l (Hình 14). Hỏi đường kính đáy của đường ống đó là bao nhiêu mét (làm tròn kết quả đến hàng phần trăm)?

Lời giải:

Thể tích của ống trụ là: V = 1 800 000 l = 1 800 000 dm³ = 1 800 m³.

Chiều cao của hình trụ là h = 30 (m).

Ta có công thức tính thể tích của hình trụ khi biết bán kính đáy và chiều cao là:

V = πr²h, suy ra $r^2=\frac{V}{\pi h}=\frac{1800}{\pi \cdot 30}=\frac{60}{\pi }$

Suy ra $r=\sqrt{\frac{60}{\pi }}=\frac{2\sqrt{15\pi }}{\pi }\text{ (m).}$

Do đó, đường kính đáy của đường ống đó là:

$2r=2\cdot \frac{2\sqrt{15\pi }}{\pi }=\frac{4\sqrt{15\pi }}{\pi }\text{ (m)}\approx 8,74\text{ (m).}$

Bài 6 trang 97 Toán 9 Tập 2: Pin là nguồn năng lượng phổ biến được sử dụng trong nhiều dụng cụ và thiết bị trong gia đình. Pin AAA (hay pin 3A) là một loại pin khô, thường được dùng trong những thiết bị điện tử cầm tay, chẳng hạn, điều khiển từ xa ti vi, máy nghe nhạc MP3, ... Mỗi chiếc pin 3A có dạng hình trụ (Hình 15), với kích cỡ tiêu chuẩn: chiều cao khoảng 44,5 mm và đường kính đáy khoảng 10,5 mm. Tính diện tích xung quanh, diện tích toàn phần (theo đơn vị centimét vuông) và thể tích (theo đơn vị centimét khối) của một chiếc pin 3A đó (làm tròn kết quả đến hàng phần mười).

Lời giải:

Bán kính đáy của chiếc pin 3A có dạng hình trụ là:

r = 10,5 : 2 = 5,25 (mm).

Diện tích xung quanh của chiếc pin 3A có hình trụ là:

S_xq = 2π.5,25.44,5 = 467,25π (mm²) = 4,6725π (cm²) ≈ 14,7 (cm²).

Diện tích toàn phần của chiếc pin 3A có hình trụ là:

S_tp = 2π.5,25.(44,5 + 5,25) = 522,375π (mm²) = 5,22375π (cm²) ≈ 16,4 (cm²).

Thể tích của chiếc pin 3A có hình trụ là:

V = π.5,25².44,5 = 1 226,53125π (mm³) = 1,22653125π (cm³) ≈ 3,9 (cm³).

Xem thêm Lời giải bài tập Toán 9 Cánh diều hay, chi tiết khác:

Bài tập cuối chương 9

Bài 2: Hình nón

Bài 3: Hình cầu

Bài tập cuối chương 10

Chủ đề 3: Tạo đồ dùng dạng hình nón, hình trụ