Giải Toán 9 Bài 1 (Cánh diều): Đa giác đều. Hình đa giác đều trong thực tiễn
Với giải bài tập Toán 9 Bài 1: Đa giác đều. Hình đa giác đều trong thực tiễn sách Cánh diều hay nhất, chi tiết giúp học sinh dễ dàng làm bài tập Toán 9.
Giải bài tập Toán 9 Bài 1: Đa giác đều. Hình đa giác đều trong thực tiễn
Khởi động trang 80 Toán 9 Tập 2: Ở lớp dưới, ta đã làm quen với những hình có dạng tam giác đều (Hình 1), hình vuông (Hình 2), lục giác đều (Hình 3). Tam giác đều, hình vuông, lục giác đều là những đa giác đều đặc biệt.
Đa giác đều là đa giác như thế nào?
Lời giải:
Sau bài học này, chúng ta sẽ trả lời được câu hỏi trên như sau:
Đa giác đều là đa giác có tất cả các cạnh bằng nhau và tất cả các góc bằng nhau.
I. Đa giác, đa giác lồi
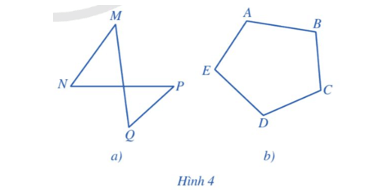
Hoạt động 1 trang 80 Toán 9 Tập 2: Tứ giác MNPQ ở Hình 4a gồm 4 đỉnh M, N, P, Q và 4 cạnh MN, NP, PQ, QM. Ngũ giác ABCDE ở Hình 4b gồm 5 đỉnh A, B, C, D, E và 5 cạnh AB, BC, CD, DE, EA.
Quan sát hai hình đó, hãy cho biết các phát biểu sau là đúng hay sai:
a) Mỗi đỉnh là điểm chung của đúng hai cạnh.
b) Không có hai cạnh nào nằm trên cùng một đường thẳng.
Lời giải:
a) – Hình 4a:
⦁ đỉnh M là điểm chung của 2 cạnh MN, MQ;
⦁ đỉnh N là điểm chung của 2 cạnh NM, NP;
⦁ đỉnh P là điểm chung của 2 cạnh PN, PQ;
⦁ đỉnh Q là điểm chung của 2 cạnh QM, QP.
– Hình 4b:
⦁ đỉnh A là điểm chung của 2 cạnh AB, AE;
⦁ đỉnh B là điểm chung của 2 cạnh BA, BC;
⦁ đỉnh C là điểm chung của 2 cạnh CB, CD;
⦁ đỉnh D là điểm chung của 2 cạnh DC, DE;
⦁ đỉnh E là điểm chung của 2 cạnh EA, ED.
Vậy phát biểu a) là đúng.
b) Trong cả hai hình, không có hai cạnh nào nằm trên cùng một đường thẳng.
Vậy phát biểu b) là đúng.
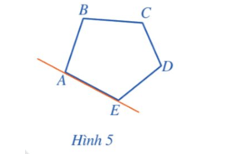
Hoạt động 2 trang 81 Toán 9 Tập 2: Nêu đặc điểm về vị trí của ngũ giác ABCDE so với đường thẳng chứa một cạnh bất kì của ngũ giác đó (Hình 5).
Lời giải:
Ngũ giác ABCDE luôn nằm về một phía so với đường thẳng chứa một cạnh bất kì của ngũ giác đó.
II. Đa giác đều
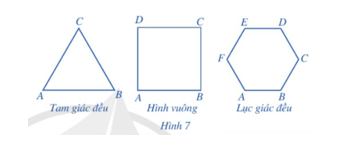
Hoạt động 3 trang 82 Toán 9 Tập 2: Quan sát Hình 7 và nêu đặc điểm về cạnh và góc của tam giác đều, hình vuông, lục giác đều.
Lời giải:
Tam giác đều ABC có AB = BC = CA và
Hình vuông ABCD có AB = BC = CD = DA và
Lục giác đều ABCDE có AB = BC = CD = DE = EF = FA và
Vậy các hình tam giác đều, hình vuông, lục giác đều có tất cả các cạnh bằng nhau và tất cả các góc bằng nhau.
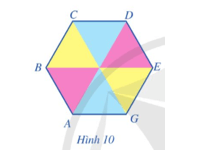
Luyện tập trang 83 Toán 9 Tập 2: Ghép sáu miếng phẳng hình tam giác đều có cạnh bằng nhau để tạo thành hình lục giác ABCDEG như ở Hình 10. Lục giác ABCDEG có là lục giác đều hay không? Vì sao?
Lời giải:
Vì lục giác ABCDEG được ghép bởi 6 hình tam giác đều có cạnh bằng nhau nên ta có AB = BC = CD = DE = EG = GA.
Mặt khác, mỗi góc trong một tam giác đều bằng 60°, nên số đo mỗi góc của lục giác là: 60° + 60° = 120°.
Vậy lục giác ABCDEG có 6 cạnh bằng nhau và 6 góc bằng nhau (cùng bằng 120°) nên ABCDEG là lục giác đều.
Bài tập
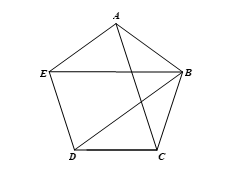
Bài 1 trang 85 Toán 9 Tập 2: Cho ngũ giác ABCDE có các cạnh bằng nhau và Ngũ giác ABCDE có phải là ngũ giác đều hay không?
Lời giải:
⦁ Do ngũ giác ABCDE có các cạnh bằng nhau nên AB = BC = CD = DE = EA.
Xét ∆ABE có AB = AE nên ∆ABE cân tại A, suy ra
Lại có (tổng ba góc của một tam giác)
Suy ra
Chứng minh tương tự với ∆BCD ta cũng có
Ta có:
Suy ra
⦁ Xét ∆ABE và ∆CDB có:
AB = CD; AE = CB
Do đó ∆ABE = ∆CDB (c.g.c)
Suy ra BE = BD (hai cạnh tương ứng)
Nên ∆BDE cân tại B, suy ra
Lại có (tổng ba góc của một tam giác)
Suy ra
Khi đó:
Và
Như vậy,
Vậy ngũ giác ABCDE có 5 cạnh bằng nhau và 5 góc bằng nhau nên ABCDE là ngũ giác đều.
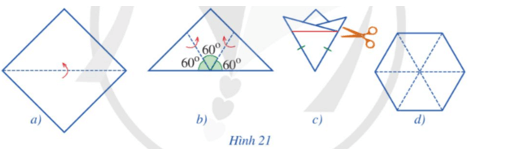
Bài 2 trang 85 Toán 9 Tập 2: Bạn Đan gấp một tờ giấy (có dạng hình vuông) lần lượt theo Hình 21a và Hình 21b để được Hình 21c, rồi cắt theo đoạn thẳng màu đỏ như ở Hình 21c, sau đó mở ra và được tờ giấy như Hình 21d. Bạn Đan cho rằng đó là một lục giác đều. Theo em, bạn Đan nói đúng hay không?
Lời giải:
Theo cách bạn Đan làm thì khi mở ra sẽ được một hình lục giác tạo bởi 6 tam giác đều (tam giác cân có góc ở đỉnh là 60°) nên theo kết quả của Luyện tập, trang 83, SGK Toán lớp 9, Tập 2 thì hình được tạo ra chính là một lục giác đều.
Bài 3 trang 85 Toán 9 Tập 2: Hãy tìm hiểu trong tự nhiên hay trong nghệ thuật, trang trí, thiết kế, công nghệ, ... những vật thể mà cấu trúc của nó có dạng hình đa giác đều.
Lời giải:
Trong tự nhiên hay trong nghệ thuật, trang trí, thiết kế, công nghệ, một số vật thể mà cấu trúc của nó có dạng hình đa giác đều để tạo ra sự đối xứng cân bằng như:
⦁ Tam giác đều: Biển báo giao thông; mặt kim tự tháp; kệ sách hình tam giác; khuôn đặt bi-a; một số thiết kế trang trí nghệ thuật;…
⦁ Hình vuông: Viên gạch lát nền; mặt bàn; mặt ghế; mặt xúc sắc; cái đĩa hình vuông.
⦁ Lục giác đều: Đèn trần; hộp đựng bánh kẹo Tết; nhiều trang trí hình lục giác đều.
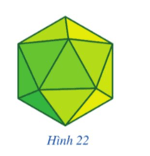
Bài 4 trang 85 Toán 9 Tập 2: Thiết kế một đồ vật từ những hình có dạng đa giác đều. Chẳng hạn, vẽ trên giấy 20 hình tam giác đều bằng nhau rồi cắt ra và dán lại để tạo thành chao đèn (hình 20 mặt đều), như ở Hình 22.
Lời giải:
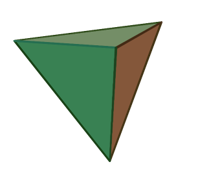
⦁ Vẽ trên giấy 4 hình tam giác đều bằng nhau rồi cắt ra và dán lại để tạo thành chao đèn (tứ diện đều):
⦁ Vẽ trên giấy 8 hình tam giác đều bằng nhau rồi cắt ra và dán lại để tạo thành chao đèn (bát diện đều):
⦁ Vẽ trên giấy 6 hình vuông bằng nhau rồi cắt ra và dán lại để tạo thành cái chao đèn (hình lập phương):
⦁ Vẽ trên giấy 12 hình ngũ giác đều bằng nhau rồi cắt ra và dán lại để tạo thành chao đèn (thập nhị diện đều):
Xem thêm Lời giải bài tập Toán 9 Cánh diều hay, chi tiết khác:
Xem thêm các chương trình khác:
- Soạn văn 9 Cánh diều (hay nhất)
- Văn mẫu 9 - Cánh diều
- Tóm tắt tác phẩm Ngữ văn 9 – Cánh diều
- Tác giả tác phẩm Ngữ văn 9 - Cánh diều
- Bố cục tác phẩm Ngữ văn 9 – Cánh diều
- Nội dung chính tác phẩm Ngữ văn 9 – Cánh diều
- Soạn văn 9 Cánh diều (ngắn nhất)
- Giải sgk Tiếng Anh 9 - ilearn Smart World
- Trọn bộ Từ vựng Tiếng Anh lớp 9 ilearn Smart World đầy đủ nhất
- Trọn bộ Ngữ pháp Tiếng Anh lớp 9 ilearn Smart World đầy đủ nhất
- Giải sbt Tiếng Anh 9 – iLearn Smart World
- Bài tập Tiếng Anh 9 iLearn Smart World theo Unit có đáp án
- Giải sgk Khoa học tự nhiên 9 – Cánh diều
- Lý thuyết Khoa học tự nhiên 9 – Cánh diều
- Giải sbt Khoa học tự nhiên 9 – Cánh diều
- Giải sgk Lịch sử 9 – Cánh diều
- Giải sbt Lịch sử 9 – Cánh diều
- Giải sgk Địa lí 9 – Cánh diều