Giải Toán 11 trang 77 Kết nối tri thức

Giải Toán 11 trang 77

Bài 4.1 trang 77 Toán 11 Tập 1: Trong không gian, cho hai đường thẳng a, b và mặt phẳng (P). Những mệnh đề nào sau đây là đúng?

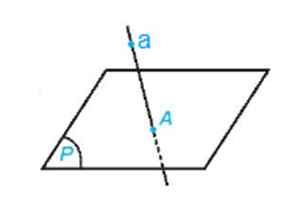
a) Nếu a chứa một điểm nằm trong (P) thì a nằm trong (P).

b) Nếu a chứa hai điểm phân biệt thuộc (P) thì a nằm trong (P).

c) Nếu a và b cùng nằm trong (P) thì giao điểm (nếu có) của a và b cũng nằm trong (P).

d) Nếu a nằm trong (P) và a cắt b thì b nằm trong (P).

Lời giải:

a) Mệnh đề a) là mệnh đề sai vì đường thẳng a có thể cắt mặt phẳng (P).

b) Mệnh đề b) là mệnh đề đúng (theo tính chất thừa nhận).

c) Mệnh đề c) là mệnh đề đúng.

Giả sử giao điểm của a và b là H, vì H thuộc a và a nằm trong (P) nên H thuộc (P).

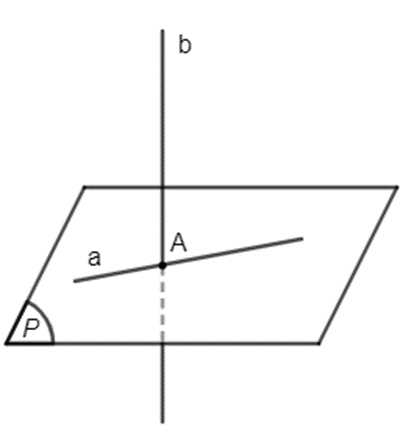
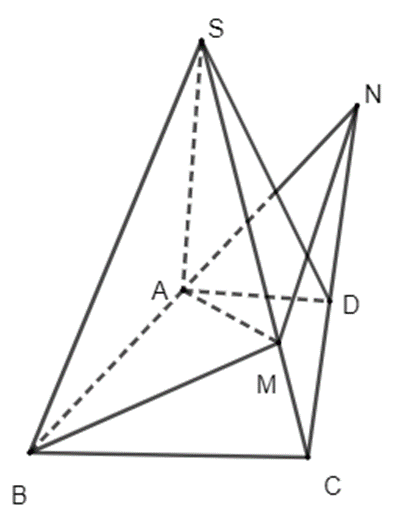
d) Mệnh đề d) là mệnh đề sai.

Chẳng hạn trường hợp như trong hình dưới đây có thể xảy ra: đường thẳng b cắt đường thẳng a tại giao điểm A nhưng đường thẳng b không nằm trong mặt phẳng (P).

Bài 4.2 trang 77 Toán 11 Tập 1: Cho tam giác ABC và điểm S không thuộc mặt phẳng (ABC). Lấy D, E là các điểm lần lượt thuộc cạnh SA, SB và D, E khác S.

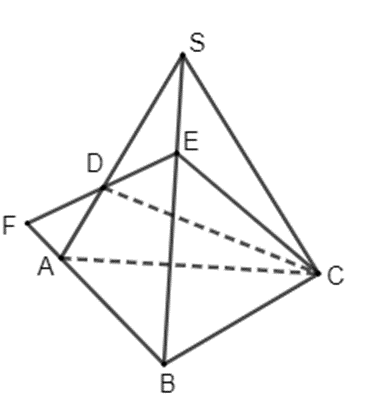
a) Đường thẳng DE có nằm trong mặt phẳng (SAB) không?

b) Giả sử DE cắt AB tại F. Chứng minh rằng F là điểm chung của hai mặt phẳng (SAB) và (CDE).

Lời giải:

a) Vì D thuộc cạnh SA nên D thuộc mặt phẳng (SAB).

Vì E thuộc cạnh SB nên E thuộc mặt phẳng (SAB).

Vì D và E cùng thuộc mặt phẳng (SAB) nên đường thẳng DE nằm trong mặt phẳng (SAB).

b) Vì F thuộc DE nên F thuộc mặt phẳng (CDE).

Vì F thuộc AB nên F thuộc mặt phẳng (SAB).

Do đó, F là điểm chung của hai mặt phẳng (SAB) và (CDE).

Bài 4.3 trang 77 Toán 11 Tập 1: Cho mặt phẳng (P) và hai đường thẳng a, b nằm trong (P). Một đường thẳng c cắt hai đường thẳng a và b tại hai điểm phân biệt. Chứng minh rằng đường thẳng c nằm trong mặt phẳng (P).

Lời giải:

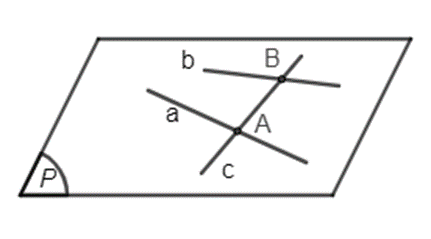
Giả sử đường thẳng c cắt hai đường thẳng a và b lần lượt tại hai điểm phân biệt A và B.

Vì A thuộc a và a nằm trong (P) nên A thuộc (P).

Vì B thuộc B và b nằm trong (P) nên B thuộc (P).

Đường thẳng c có hai điểm phân biệt A và B cùng thuộc mặt phẳng (P) nên tất cả các điểm của đường thẳng c đều thuộc (P) hay đường thẳng c nằm trong mặt phẳng (P).

Bài 4.4 trang 77 Toán 11 Tập 1: Cho hình chóp tứ giác S.ABCD và M là một điểm thuộc cạnh SC (M khác S, C). Giả sử hai đường thẳng AB và CD cắt nhau tại N. Chứng minh rằng đường thẳng MN là giao tuyến của hai mặt phẳng (ABM) và (SCD).

Lời giải:

Vì N thuộc đường thẳng AB nên N thuộc mặt phẳng (ABM), lại có M thuộc mặt phẳng (ABM) nên đường thẳng MN nằm trong mặt phẳng (ABM) (1).

Vì N thuộc đường thẳng CD nên N thuộc mặt phẳng (SCD), vì M thuộc cạnh SC nên M thuộc mặt phẳng (SCD), do đó đường thẳng MN nằm trong mặt phẳng (SCD) (2).

Từ (1) và (2) suy ra đường thẳng MN là giao tuyến của hai mặt phẳng (ABM) và (SCD).

Bài 4.5 trang 77 Toán 11 Tập 1: Cho hình chóp tứ giác S.ABCD và lấy một điểm E thuộc cạnh SA của hình chóp (E khác S, A). Trong mặt phẳng (ABCD) vẽ một đường thẳng d cắt các cạnh CB, CD lần lượt tại M, N và cắt các tia AB, AD lần lượt tại P, Q.

a) Xác định giao điểm của mp(E, d) với các cạnh SB, SD của hình chóp.

b) Xác định giao tuyến của mp(E, d) với các mặt của hình chóp.

Lời giải:

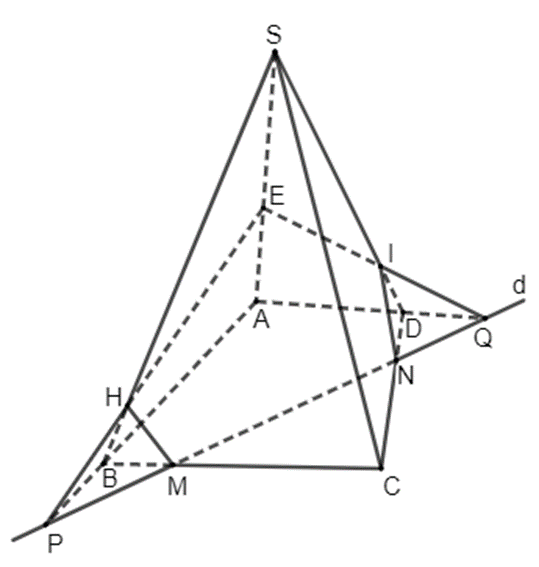
a) +) Vì E thuộc cạnh SA nên E thuộc mặt phẳng (SAB). Vì P thuộc đường thẳng AB nên P thuộc mặt phẳng (SAB). Như vậy, các điểm S, A, B, E, P cùng thuộc mặt phẳng (SAB).

Trong tam giác SAB, đường thẳng EP cắt cạnh SB tại một điểm H. Do P thuộc đường thẳng d nên EP nằm trong mp(E, d) và H thuộc EP, do đó H thuộc mp(E, d). Vậy H là giao điểm của đường thẳng SB và mp(E, d).

+) Vì E thuộc cạnh SA nên E thuộc mặt phẳng (SAD). Vì Q thuộc đường thẳng AD nên Q thuộc mặt phẳng (SAD). Như vậy, các điểm S, A, D, E, Q cùng thuộc mặt phẳng (SAD).

Trong tam giác SAD, đường thẳng EQ cắt cạnh SD tại một điểm I. Do Q thuộc đường thẳng d nên EQ nằm trong mp(E, d) và I thuộc EQ, do đó I thuộc mp(E, d). Vậy I là giao điểm của đường thẳng SD và mp(E, d).

b)

+) Đường thẳng d cắt các cạnh CB, CD lần lượt tại M, N, do đó M, N thuộc d, mà d nằm trong mp(E, d) nên đường thẳng MN cũng nằm trong mp(E, d). Ta lại có, M thuộc CB nằm trong mặt phẳng (ABCD) nên M thuộc mặt phẳng (ABCD), tương tự N thuộc CD nằm trong mặt phẳng (ABCD) nên N thuộc mặt phẳng (ABCD), do đó đường thẳng MN nằm trong mặt phẳng (ABCD). Vậy MN là giao tuyến của hai mặt phẳng (ABCD) và mp(E, d).

+) Vì H thuộc SB nằm trong mặt phẳng (SAB) nên H thuộc mặt phẳng (SAB), lại có E thuộc mặt phẳng (SAB), do đó EH nằm trong mặt phẳng (SAB). Vì E thuộc mp(E, d) và H thuộc mp(E, d) nên EH nằm trong mp(E, d). Vậy EH là giao tuyến của hai mặt phẳng (SAB) và mp(E, d).

+) Vì I thuộc SD nằm trong mặt phẳng (SAD) nên I thuộc mặt phẳng (SAD), lại có E thuộc mặt phẳng (SAD), do đó EI nằm trong mặt phẳng (SAD). Vì E thuộc mp(E, d) và I thuộc mp(E, d) nên EI nằm trong mp(E, d). Vậy EI là giao tuyến của hai mặt phẳng (SAD) và mp(E, d).

+) Vì H thuộc SB nên H thuộc mặt phẳng (SBC), vì M thuộc BC nên M thuộc mặt phẳng (SBC), do đó HM nằm trong mặt phẳng (SBC). Lại có M thuộc d nên M thuộc mp(E, d) và H thuộc mp(E, d) nên HM nằm trong mp(E, d). Vậy HM là giao tuyến của hai mặt phẳng (SBC) và mp(E, d).

+) Vì I thuộc SD nên I thuộc mặt phẳng (SCD), vì N thuộc CD nên N thuộc mặt phẳng (SCD), do đó IN nằm trong mặt phẳng (SCD). Lại có N thuộc d nên N thuộc mp(E, d) và I thuộc mp(E, d) nên IN nằm trong mp(E, d). Vậy IN là giao tuyến của hai mặt phẳng (SCD) và mp(E, d).

Bài 4.6 trang 77 Toán 11 Tập 1: Cho hình tứ diện ABCD. Trên các cạnh AC, BC, BD lần lượt lấy các điểm M, N, P sao cho AM = CM, BN = CN, BP = 2DP.

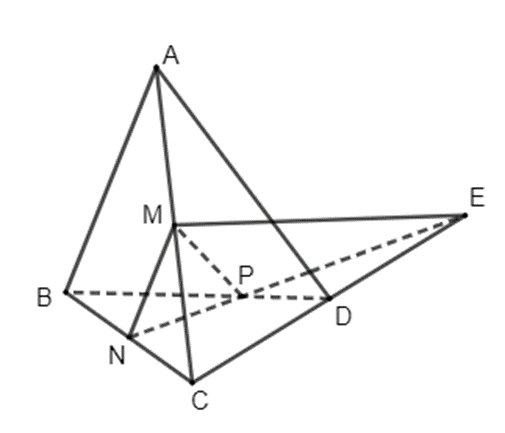
a) Xác định giao điểm của đường thẳng CD và mặt phẳng (MNP).

b) Xác định giao tuyến của hai mặt phẳng (ACD) và (MNP).

Lời giải:

a) Trong tam giác BCD, N thuộc cạnh BC thỏa mãn BN = CN hay N là trung điểm của BC và P thuộc cạnh BD sao cho BP = 2DP. Khi đó, đường thẳng NP cắt CD tại một điểm E. Vì E thuộc NP nằm trong mặt phẳng (MNP) nên E thuộc mặt phẳng (MNP). Vậy E là giao điểm của đường thẳng CD và mặt phẳng (MNP).

b) Vì M thuộc cạnh AC nên M thuộc mặt phẳng (ACD), vì E thuộc CD nên E thuộc mặt phẳng (ACD), do đó đường thẳng ME nằm trong mặt phẳng (ACD).

Vì E thuộc mặt phẳng (MNP) và M thuộc mặt phẳng (MNP) nên ME nằm trong mặt phẳng (MNP).

Vậy ME là giao tuyến của hai mặt phẳng (ACD) và (MNP).

Bài 4.7 trang 77 Toán 11 Tập 1: Tại các nhà hàng, khách sạn, nhân viên phục vụ bàn thường xuyên phải bưng bê nhiều khay, đĩa đồ ăn khác nhau. Một trong những nguyên tắc nhân viên cần nhớ là khay phải được bưng bằng ít nhất 3 ngón tay. Hãy giải thích tại sao?

Lời giải:

Ba đầu ngón tay minh họa cho 3 điểm phân biệt không thẳng hàng. Theo tính chất thừa nhận, có một và chỉ một mặt phẳng đi qua ba điểm không thẳng hàng. Khi đó, mỗi khay, đĩa đồ ăn đại diện cho một mặt phẳng đi qua ba điểm ở đầu ngón tay làm cho khay, đĩa đồ ăn được giữ vững bằng phẳng.

Bài 4.8 trang 77 Toán 11 Tập 1: Bàn cắt giấy là một dụng cụ được sử dụng thường xuyên ở các cửa hàng photo-copy. Bàn cắt giấy gồm hai phần chính: phần bàn hình chữ nhật có kích thước giấy và phần dao cắt có một đầu được cố định vào bàn. Hãy giải thích tại sao khi sử dụng bàn cắt giấy thì các đường cắt luôn là đường thẳng.

Lời giải:

Phần dao cắt có một đầu được gắn cố định vào bàn, giấy cắt được đặt lên phần bàn hình chữ nhật, khi cắt mặt phẳng cắt giao với mặt phẳng giấy theo một giao tuyến là phần đường cắt nên nó luôn là một đường thẳng.

Xem thêm lời giải bài tập Toán 11 Kết nối tri thức hay, chi tiết khác: 

Giải Toán 11 trang 71

Giải Toán 11 trang 72

Giải Toán 11 trang 73

Giải Toán 11 trang 74

Giải Toán 11 trang 75

Giải Toán 11 trang 76

Giải Toán 11 trang 77