Giải SBT Toán 10 trang 70 Tập 2 Kết nối tri thức

Giải SBT Toán 10 trang 70 Tập 2 Kết nối tri thức

Bài 1 trang 70 SBT Toán 10 Tập 2: Cho các mệnh đề:

P: “Phương trình bậc hai ax² + bx + c = 0 có hai nghiệm phân biệt”;

Q: “Phương trình bậc hai ax² + bx + c = 0 có biệt thức ∆ = b² – 4ac > 0”.

a) Hãy phát biểu các mệnh đề: P ⇒ Q, Q ⇒ P, P ⇔ Q, $\overline{P}\Rightarrow \overline{Q}$ . Xét tính đúng sai của các mệnh đề này.

b) Dùng các khái niệm “điều kiện cần” và “điều kiện đủ” để diễn tả mệnh đề P ⇒ Q.

c) Gọi X là tập hợp các phương trình bậc hai ax² + bx + c = 0 có hai nghiệm phân biệt, Y là tập hợp các phương trình bậc hai ax² + bx + c = 0 có hệ số a và c trái dấu. Nêu mối quan hệ giữa hai tập hợp X và Y.

Lời giải:

a)

+ Mệnh đề P ⇒ Q: “Nếu phương trình bậc hai ax² + bx + c = 0 có hai nghiệm phân biệt thì phương trình bậc hai ax² + bx + c = 0 có biệt thức ∆ = b² – 4ac > 0”. Đây là mệnh đề đúng.

+ Mệnh đề Q ⇒ P: “ Nếu phương trình bậc hai ax² + bx + c = 0 có biệt thức ∆ = b² – 4ac > 0 thì phương trình bậc hai ax² + bx + c = 0 có hai nghiệm phân biệt”. Đây là mệnh đề đúng.

+ Mệnh đề P ⇔ Q: “Phương trình bậc hai ax² + bx + c = 0 có hai nghiệm phân biệt khi và chỉ khi phương trình bậc hai ax² + bx + c = 0 có biệt thức ∆ = b² – 4ac > 0”. Do P ⇒ Q, Q ⇒ P đều là các mệnh đề đúng nên mệnh đề P ⇔ Q là mệnh đề đúng.

+ Mệnh đề $\overline{P}\Rightarrow \overline{Q}$

Mệnh đề $\overline{P}$  là mệnh đề phủ định của mệnh đề P và được phát biểu là: “Phương trình bậc hai ax² + bx + c = 0 không có hai nghiệm phân biệt”.

Mệnh đề $\overline{Q}$  là mệnh đề phủ định của mệnh đề Q và được phát biểu là: “Phương trình bậc hai ax² + bx + c = 0 có biệt thức ∆ = b² – 4ac ≤ 0”.

Khi đó, ta phát biểu mệnh đề $\overline{P}\Rightarrow \overline{Q}$ : “Nếu phương trình bậc hai ax² + bx + c = 0 không có hai nghiệm phân biệt thì phương trình bậc hai ax² + bx + c = 0 có biệt thức ∆ = b² – 4ac ≤ 0”. Mệnh đề này là mệnh đề đúng.

b)

+ Phương trình bậc hai ax² + bx + c = 0 có hai nghiệm phân biệt là điều kiện đủ để phương trình bậc hai ax² + bx + c = 0 có biệt thức ∆ = b² – 4ac > 0.

+ Phương trình bậc hai ax² + bx + c = 0 có biệt thức ∆ = b² – 4ac > 0 là điều kiện cần để phương trình bậc hai ax² + bx + c = 0 có hai nghiệm phân biệt.

c) Ta có các phương trình bậc hai ax² + bx + c = 0 có hệ số a và c trái dấu thì luôn có hai nghiệm trái dấu, hiển nhiên đây là hai nghiệm phân biệt. Nhưng các phương trình bậc hai ax² + bx + c = 0 có hai nghiệm phân biệt thì hai nghiệm này chưa chắc đã trái dấu.

Do đó mọi phần tử của tập hợp Y thì đều là phần tử của tập hợp X.

Vậy Y là tập con của tập hợp X và ta viết Y ⊂ X.

Bài 2 trang 70 SBT Toán 10 Tập 2: a) Biểu diễn hình học tập nghiệm D của hệ bất phương trình bậc nhất hai ẩn sau:

$\left\{\begin{array}{c}x\ge 0\\ y\ge 0\\ 3x-2y\ge -6\\ 2x+y\le 10\end{array}\right.$.

b) Từ kết quả ở câu a), tìm giá trị lớn nhất và giá trị nhỏ nhất của biểu thức F(x; y) = 2x + 3y trên miền D, biết rằng giá trị lớn nhất (tương ứng, nhỏ nhất) của F đạt được tại một trong các đỉnh của miền đa giác D.

Lời giải:

a) Ta xác định miền nghiệm của từng bất phương trình trong hệ đã cho như sau:

Bước 1: Trục Oy có phương trình x = 0 và điểm (1; 0) thỏa mãn 1 > 0. Do đó miền nghiệm của bất phương trình x ≥ 0 là nửa mặt phẳng bờ Oy chứa điểm (1; 0) (miền không bị gạch).

Bước 2: Trục Ox có phương trình y = 0 và điểm (0; 1) thỏa mãn 1 > 0. Do đó, miền nghiệm của bất phương trình y ≥ 0 là nửa mặt phẳng bờ Ox chứa điểm (0; 1) (miền không bị gạch).

Bước 3: Vẽ đường thẳng d₁: 3x – 2y = – 6. Lấy điểm O(0; 0) không thuộc d₁ và thay x = 0, y = 0 vào biểu thức 3x – 2y ta được: 3 . 0 – 2 . 0 = 0 > – 6. Do đó, miền nghiệm của bất phương trình 3x – 2y ≥ – 6 là nửa mặt phẳng bờ d₁ chứa điểm O(0; 0) (miền không bị gạch).

Bước 4: Vẽ đường thẳng d₂: 2x + y = 10. Lấy điểm O(0; 0) không thuộc d₂ và thay x = 0, y = 0 vào biểu thức 2x + y ta được: 2 . 0 + 0 = 0 < 10. Do đó, miền nghiệm của bất phương trình 2x + y ≤ 10 là nửa mặt phẳng bờ d₂ chứa điểm O(0; 0) (miền không bị gạch).

Vậy miền nghiệm D của hệ bất phương trình đã cho là miền tứ giác OABC (miền không bị gạch), trong đó A(0; 3), B(2; 6), C(5; 0), như hình vẽ sau:

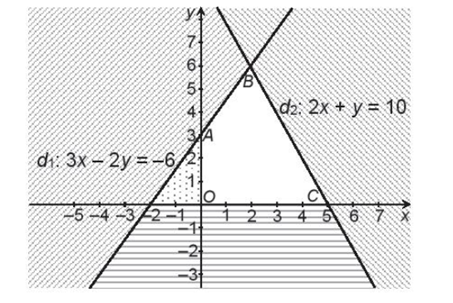
b) Vì giá trị lớn nhất (tương ứng, nhỏ nhất) của F đạt được tại một trong các đỉnh của miền đa giác D, do đó ta tính giá trị của F tại (x; y) là tọa độ các đỉnh O, A, B, C.

Ta có: F(0; 0) = 2 . 0 + 3 . 0 = 0;

F(0; 3) = 2 . 0 + 3 . 3 = 9;

F(2; 6) = 2 . 2 + 3 . 6 = 22;

F(5; 0) = 2 . 5 + 3 . 0 = 10.

Vậy giá trị lớn nhất và giá trị nhỏ nhất của biểu thức F(x; y) = 2x + 3y trên miền D lần lượt là 22 và 0.

Bài 3 trang 70 SBT Toán 10 Tập 2: Cho tam thức bậc hai f(x) = ax² + bx + c với đồ thị là parabol có đỉnh I(1; 4) và đi qua điểm A(2; 3).

a) Xác định các hệ số a, b, c của tam thức bậc hai f(x).

b) Vẽ parabol này.

c) Từ đồ thị đã vẽ ở câu b), hãy cho biết khoảng đồng biến, khoảng nghịch biến và tập giá trị của hàm số y = f(x).

d) Lập bảng xét dấu để giải bất phương trình $\frac{f\left(x\right)}{x-2}\ge 0$ .

Lời giải:

a) Parabol có đỉnh là I(1; 4) nên có phương trình dạng y = a(x – 1)² + 4.

Vì điểm A(2; 3) thuộc parabol nên ta có:

3 = a(2 – 1)² + 4 ⇔ a + 4 = 3 ⇔ a = – 1.

Vậy tam thức bậc hai cần tìm là f(x) = –(x – 1)² + 4 hay f(x) = – x² + 2x + 3.

Suy ra các hệ số là: a = – 1; b = 2; c = 3.

b) Ta có: a = – 1 < 0 nên parabol quay bề lõm xuống dưới.

Đỉnh parabol là I(1; 4).

Trục đối xứng x = 1.

Giao điểm của parabol với trục Oy là (0; 3). Điểm đối xứng với điểm (0; 3) qua trục đối xứng x = 1 là (2; 3).

Giao điểm của parabol với trục Ox là (– 1; 0) và (3; 0).

Vẽ đường cong đi qua các điểm trên ta được parabol cần vẽ.

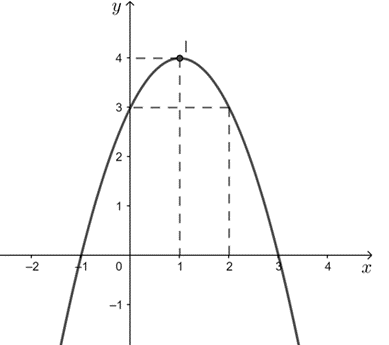
c) Từ đồ thị trên ta thấy:

- Hàm số đồng biến trên khoảng (– ∞; 1) và nghịch biến trên khoảng (1; + ∞).

- Tập giá trị của hàm số là (– ∞; 4].

d) Xét bất phương trình $\frac{f\left(x\right)}{x-2}\ge 0$ , hay $\frac{-x^2+2x+3}{x-2}\ge 0$ .

Tam thức f(x) = – x² + 2x + 3 có ∆' = 1² – (– 1) . 3 = 4 > 0 và a = – 1 < 0, f(x) có hai nghiệm phân biệt x₁ = – 1 và x₂ = 3. Do đó, f(x) > 0 với mọi x ∈ (– 1; 3) và f(x) < 0 với mọi x ∈ (– ∞; – 1) ∪ (3; + ∞).

Ta có bảng xét dấu sau:

 Vậy tập nghiệm của bất phương trình đã cho là S = (– ∞; – 1] ∪ (2; 3].

Xem thêm lời giải sách bài tập Toán lớp 10 Kết nối tri thức với cuộc sống hay, chi tiết khác: 

Giải SBT Toán 10 trang 71 Tập 2

Giải SBT Toán 10 trang 72 Tập 2

Giải SBT Toán 10 trang 73 Tập 2