Nội dung bài viết

    Xem thêm

    Sách bài tập Toán 7 Bài 2 (Chân trời sáng tạo): Tam giác bằng nhau

    Với giải sách bài tập Toán 7 Bài 2: Tam giác bằng nhau sách Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập trong SBT Toán 7 Bài 2.

    1 2,597 01/01/2023
    Trang trước
    Chia sẻ
    Trang sau  

    Giải sách bài tập Toán lớp 7 Bài 2: Tam giác bằng nhau

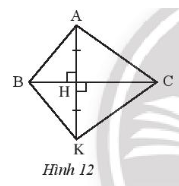
    Bài 1 trang 45 SBT Toán 7 Tập 2: Trong Hình 12, tìm tam giác bằng tam giác ABH.

    Sách bài tập Toán 7 Bài 2 (Kết nối tri thức): Tam giác bằng nhau (ảnh 1)

    Lời giải

    Xét ∆ABH và ∆KBH có:

    BHA^=BHK^ (cùng bằng 90°),

    BH là cạnh chung,

    AH = HK (giả thiết).

    Do đó ΔABH = ΔKBH (hai cạnh góc vuông).

    Vậy ΔABH = ΔKBH.

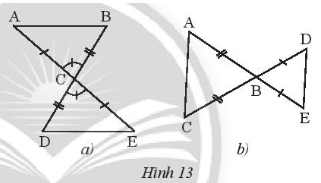
    Bài 2 trang 45 SBT Toán 7 Tập 2: Hai tam giác trong Hình 13a, 13b có bằng nhau không? Vì sao?

    Sách bài tập Toán 7 Bài 2 (Kết nối tri thức): Tam giác bằng nhau (ảnh 1)

    Lời giải

    • Hình 13a)

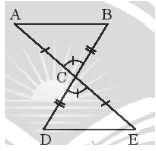
    Sách bài tập Toán 7 Bài 2 (Kết nối tri thức): Tam giác bằng nhau (ảnh 1)

    Xét ∆ABC và ∆EDC có:

    AC = EC (giả thiết),

    BCA^=DCE^ (hai góc đối đỉnh),

    BC = DC (giả thiết)

    Do đó ΔABC = ΔEDC (c.g.c)

    Vậy ΔABC = ΔEDC.

    • Hình 13b)

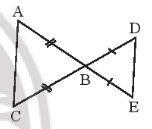
    Sách bài tập Toán 7 Bài 2 (Kết nối tri thức): Tam giác bằng nhau (ảnh 1)

    Xét ∆ABC và ∆EDB có:

    AB = BC ≠ BE = BD.

    Do đó hai tam giác ABC và EBD không bằng nhau

    Vậy hai tam giác ABC và EBD không bằng nhau.

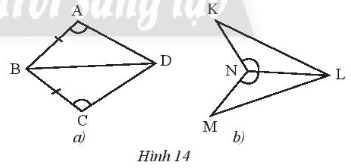
    Bài 3 trang 45 SBT Toán 7 Tập 2: Nêu thêm điều kiện để hai tam giác trong Hình 14a, 14b bằng nhau theo trường hợp cạnh – góc – cạnh.

    Sách bài tập Toán 7 Bài 2 (Kết nối tri thức): Tam giác bằng nhau (ảnh 1)

    Lời giải

    • Hình a)

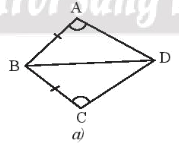
    Sách bài tập Toán 7 Bài 2 (Kết nối tri thức): Tam giác bằng nhau (ảnh 1)

    Để ∆ABD = ∆CBD theo trường hợp cạnh – góc – cạnh thì điều kiện về cặp góc bằng nhau của hai tam giác là góc xen kẽ giữa hai cạnh.

    Mà BAD^ là góc xen kẽ giữa hai cạnh AB và AD, BCD^ là góc xen kẽ giữa hai cạnh CB và CD.

    Lại có AB = CB (giả thiết).

    Do đó điều kiện còn lại là điều kiện về cạnh, đó là AD = CD.

    Vậy cần thêm điều kiện AD = CD.

    • Hình b)

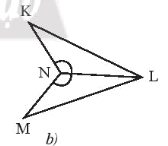
    Sách bài tập Toán 7 Bài 2 (Kết nối tri thức): Tam giác bằng nhau (ảnh 1)

    Để ∆KNL = ∆MNL theo trường hợp cạnh – góc – cạnh thì điều kiện về cặp góc bằng nhau của hai tam giác là góc xen kẽ giữa hai cạnh.

    Mà KNL^ là góc xen kẽ giữa hai cạnh NK và NL, MNL^ là góc xen kẽ giữa hai cạnh NM và NL.

    Lại có cạnh NL là cạnh chung của hai tam giác.

    Do đó điều kiện còn lại là điều kiện về cạnh, đó là NK = NM.

    Vậy cần thêm điều kiện NK = NM.

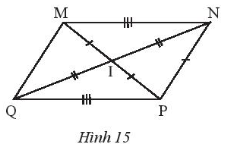
    Bài 4 trang 45 SBT Toán 7 Tập 2: Quan sát Hình 15 rồi thay dấu ? bằng tên tam giác thích hợp.

    Sách bài tập Toán 7 Bài 2 (Kết nối tri thức): Tam giác bằng nhau (ảnh 1)

    a) ∆MNI = ∆?;

    b) ∆INM = ∆?;

    c) ∆? = ∆QIP.

    Lời giải

    a) Xét ∆MNI và ∆PQI có:

    MN = PQ (giả thiết),

    MI = PI (giả thiết),

    NI = QI (giả thiết).

    Do đó ΔMNI = ΔPQI (c.c.c).

    Vậy ΔMNI = ΔPQI.

    b) Vì ΔMNI = ΔPQI (theo câu a) nên ΔINM = ΔIQP.

    Vậy ΔINM = ΔIQP.

    c) Vì ΔMNI = ΔPQI (theo câu a) nên ΔNIM = ΔQIP.

    Vậy ΔNIM = ΔQIP.

    Bài 5 trang 46 SBT Toán 7 Tập 2: Cho ΔABC = ΔDEF và A^=44°, EF = 7 cm, ED = 15 cm. Tính số đo D^ và độ dài BC, BA.

    Lời giải

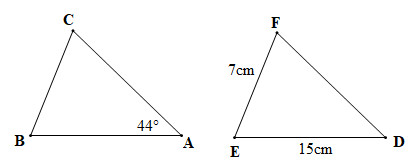
    Sách bài tập Toán 7 Bài 2 (Kết nối tri thức): Tam giác bằng nhau (ảnh 1)

    Vì ΔABC = ΔDEF (giả thiết) nên ta có:

    • A^=D^ (hai góc tương ứng);

    • BA = ED, BC = EF (các cặp cạnh tương ứng).

    Mà A^=44°, EF = 7 cm, ED = 15 cm (giả thiết).

    Suy ra D^=44°, BC = 7 cm và BA = 15 cm.

    Vậy D^=44°, BC = 7 cm và BA = 15 cm.

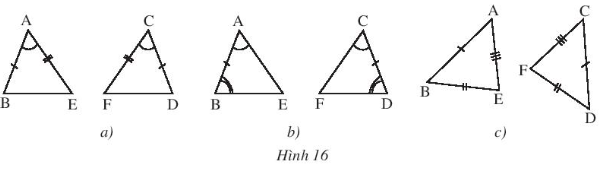
    Bài 6 trang 46 SBT Toán 7 Tập 2: Các cặp tam giác trong Hình 16 có bằng nhau không? Nếu có, chúng bằng nhau theo trường hợp nào?

    Sách bài tập Toán 7 Bài 2 (Kết nối tri thức): Tam giác bằng nhau (ảnh 1)

    Lời giải

    • Hình a)

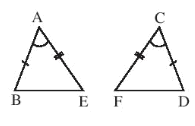
    Sách bài tập Toán 7 Bài 2 (Kết nối tri thức): Tam giác bằng nhau (ảnh 1)

    Xét ∆ABE và ∆CDF có:

    AB = CD (giả thiết),

    A^=C^ (giả thiết),

    AE = CF (giả thiết).

    Do đó ΔABE = ΔCDF (c.g.c).

    Vậy hai tam giác ABE và CDF bằng nhau theo trường hợp c.g.c.

    • Hình b)

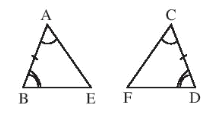
    Sách bài tập Toán 7 Bài 2 (Kết nối tri thức): Tam giác bằng nhau (ảnh 1)

    Xét ∆ABE và ∆CDF có:

    A^=C^ (giả thiết),

    AB = CD (giả thiết),

    B^=D^ (giả thiết).

    Do đó ΔABE = ΔCDF (g.c.g).

    Vậy hai tam giác ABE và CDF bằng nhau theo trường hợp g.c.g.

    • Hình c)

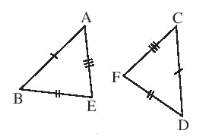
    Sách bài tập Toán 7 Bài 2 (Kết nối tri thức): Tam giác bằng nhau (ảnh 1)

    Xét ∆ABE và ∆CDF có:

    AE = CF (giả thiết),

    AB = CD (giả thiết),

    BE = DF (giả thiết).

    Do đó ΔABE = ΔCDF (c.c.c).

    Vậy hai tam giác ABE và CDF bằng nhau theo trường hợp c.c.c.

    Bài 7 trang 46 SBT Toán 7 Tập 2: Cho biết ΔABC = ΔDEF và AB = 9 cm, AC = 7 cm, EF = 10 cm. Tính chu vi tam giác ABC.

    Lời giải

    Vì ΔABC = ΔDEF (giả thiết)

    Nên BC = EF (hai cạnh tương ứng).

    Mà EF = 10 cm (giả thiết).

    Suy ra BC = 10 cm.

    Chu vi tam giác ABC là:

    AB + BC + CA = 9 + 10 + 7 = 26 (cm).

    Vậy chu vi tam giác ABC là 26 cm.

    Bài 8 trang 46 SBT Toán 7 Tập 2: Cho tam giác ABC có AB = AC, lấy điểm M trên cạnh BC sao cho BM = CM. Chứng minh hai tam giác ABM và ACM bằng nhau.

    Lời giải

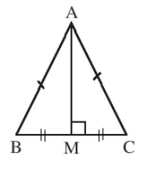
    Sách bài tập Toán 7 Bài 2 (Kết nối tri thức): Tam giác bằng nhau (ảnh 1)

    Xét ∆ABM và ∆ACM có:

    AB = AC (giả thiết),

    BM = CM (giả thiết),

    AM là cạnh chung.

    Do đó ΔABM = ΔACM (c.c.c).

    Vậy ΔABM = ΔACM.

    Bài 9 trang 46 SBT Toán 7 Tập 2: Cho góc xOy. Lấy hai điểm A, B thuộc tia Ox sao cho OA < OB. Lấy hai điểm C, D thuộc tia Oy sao cho OA = OC, OB = OD. Gọi M là giao điểm của AD và CB. Chứng minh rằng:

    a) AD = CB;

    b) ΔMAB = ΔMCD.

    Lời giải

    GT

    xOy^ nhọn,

    A ∈ Ox, B ∈ Ox, OA < OB.

    C ∈ Oy, D ∈ Oy, OA = OC, OB = OD.

    AD cắt BC tại M.

    KL

    a) AD = CB;

    b) ΔMAB = ΔMCD.

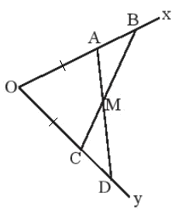
    Sách bài tập Toán 7 Bài 2 (Kết nối tri thức): Tam giác bằng nhau (ảnh 1)

    a) Xét ∆AOD và ∆COB có:

    OA = OC (giả thiết),

    O^ là góc chung,

    OD = OB (giả thiết).

    Do đó ΔAOD = ΔCOB (c.g.c).

    Suy ra AD = CB (hai cạnh tương ứng).

    Vậy AD = CB.

    b) Ta có OB = OA + AB (do OA < OB) nên AB = OB – OA.

    Tương tự OD = OC + CD nên CD = OD – OC.

    Mà OA = OC, OB = OD (giả thiết).

    Suy ra AB = CD.

    Vì ΔAOD = ΔCOB (chứng minh câu a).

    Nên ADO^=CBO^,  DAO^=BCO^ (các cặp góc tương ứng) (1)

    Ta có DAO^+DAB^=180° (hai góc kề bù)

    Suy ra DAB^=180°−DAO^       (2)

    Ta có BCO^+BCD^=180° (hai góc kề bù)

    Hay BCD^=180°−BCO^           (3)

    Từ (1), (2), (3) suy ra DAB^=BCD^.

    Xét ΔMAB và ΔMCD có

    MAB^=MCD^ (do DAB^=BCD^),

    AB = CD (chứng minh trên),

    MBA^=MDC^ (do CBO^=ADO^).

    Do đó ΔMAB = ΔMCD (g.c.g).

    Vậy ΔMAB = ΔMCD.

    Xem thêm lời giải sách bài tập Toán lớp 7 bộ sách Chân trời sáng tạo hay, chi tiết nhất:

    Bài 3: Tam giác cân

    Bài 4: Đường vuông góc và đường xiên

    Bài 5: Đường trung trực của một đoạn thẳng

    Bài 6: Tính chất ba đường trung trực của tam giác

    Bài 7: Tính chất ba đường trung tuyến của tam giác

    Tham khảo các loạt bài Toán 7 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 2,597 01/01/2023
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: