Sách bài tập Toán 7 (Chân trời sáng tạo) Bài tập cuối chương 4

Giải sách bài tập Toán lớp 7 Bài tập cuối chương 4 - Chân trời sáng tạo

Giải SBT Toán 7 trang 87 Tập 1

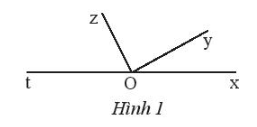
Bài 1 trang 87 Sách bài tập Toán 7 Tập 1:

a) Đo các góc trong Hình 1.

b) Nêu tên các cặp góc kề bù.

Lời giải

a) Sử dụng thước đo góc ta đo được $\widehat{xOy}=30°,\widehat{yOz}=90°,$$\widehat{zOt}=60°,$$\widehat{xOz}=120°,$$\widehat{yOt}=150°$ và $\widehat{xOt}=180°.$

b) Các cặp góc kề bù có trong hình là: $\widehat{xOy}$ kề bù với $\widehat{yOt};$ $\widehat{xOz}$ kề bù với $\widehat{zOt}.$

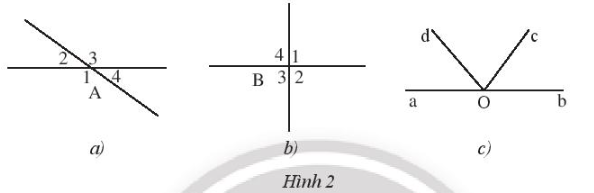
Bài 2 trang 87 Sách bài tập Toán 7 Tập 1: Hãy kể tên các cặp góc đối đỉnh trong Hình 2.

Lời giải

a) Các cặp góc đối đỉnh trong hình là: ${\widehat{A}}_1$ và ${\widehat{A}}_3;$ ${\widehat{A}}_2$ và ${\widehat{A}}_4.$

b) Các cặp góc đối đỉnh trong hình là: ${\widehat{B}}_1$ và ${\widehat{B}}_3;$ ${\widehat{B}}_2$ và ${\widehat{B}}_4.$

c) Trong hình không có cặp góc nào đối đỉnh do chỉ có tia Oa là tia đối của tia Ob nhưng tia Oc không là tia đối của tia Od.

Bài 3 trang 87 Sách bài tập Toán 7 Tập 1: Trong Hình 3 cho biết a // b. Tìm số đo các góc đỉnh A và B.

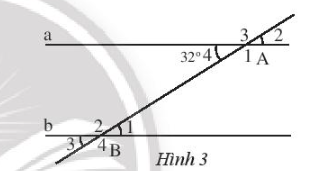
Lời giải

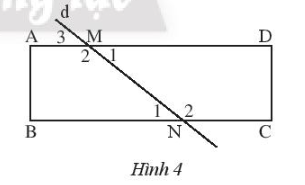
– Tại đỉnh A:

• Vì ${\widehat{A}}_2$ và ${\widehat{A}}_4$ là hai góc đối đỉnh nên ${\widehat{A}}_2={\widehat{A}}_4=32°.$

• Vì ${\widehat{A}}_1$ và ${\widehat{A}}_4$ là hai góc kề bù nên ta có:

${\widehat{A}}_1+{\widehat{A}}_4=180°$

Suy ra ${\widehat{A}}_1=180°-{\widehat{A}}_4=180°-32°=148°$

• Vì ${\widehat{A}}_1$ và ${\widehat{A}}_3$ là hai góc đối đỉnh nên ${\widehat{A}}_1={\widehat{A}}_3=148°.$

– Tại đỉnh B:

Vì a // b nên:

• ${\widehat{B}}_1={\widehat{A}}_4=32°$ (hai góc so le trong)

• ${\widehat{B}}_2={\widehat{A}}_1=148°$ (hai góc so le trong)

• ${\widehat{B}}_3={\widehat{A}}_4=32°$ (hai góc đồng vị)

• ${\widehat{B}}_4={\widehat{A}}_1=148°$ (hai góc đồng vị).

Vậy ${\widehat{A}}_1=148°,{\widehat{A}}_2=32°,{\widehat{A}}_3=148°;$ ${\widehat{B}}_1=32°,{\widehat{B}}_2=148°,{\widehat{B}}_3=32°,{\widehat{B}}_4=148°.$

Bài 4 trang 87 Sách bài tập Toán 7 Tập 1: Vẽ hình, viết giả thiết và kết luận của định lí về đường phân giác của hai góc kề bù.

Lời giải

Hình vẽ minh họa:

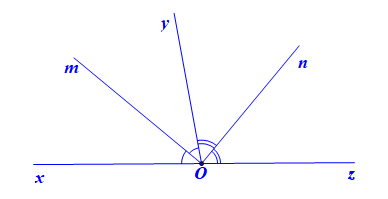
Viết giả thiết và kết luận bằng kí hiệu:

Bài 5 trang 87 Sách bài tập Toán 7 Tập 1: Cho hình chữ nhật ABCD và đường thẳng d cắt hai cạnh AD và CB như trong Hình 4.

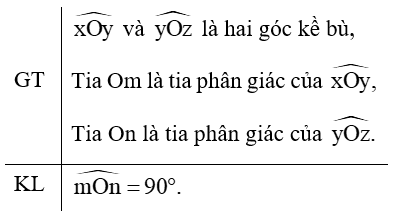
a) Tìm góc đối đỉnh của góc M₁.

b) Tìm góc kề bù của góc M₁.

c) Tìm góc đồng vị của góc M₃.

d) Tìm góc có số đo bằng số đo của góc M₁.

Lời giải   

a) Góc đối đỉnh của ${\widehat{M}}_1$ là ${\widehat{M}}_3.$

b) Góc kề bù của ${\widehat{M}}_1$ là ${\widehat{M}}_2.$

c) Góc đồng vị của ${\widehat{M}}_3.$ là ${\widehat{N}}_1.$

d) Các góc có số đo bằng số đo của ${\widehat{M}}_1$ là: ${\widehat{M}}_3$ (đối đỉnh) và ${\widehat{N}}_1.$(so le trong).

Bài 6 trang 87 Sách bài tập Toán 7 Tập 1: Cho hình thoi ABCD, biết AC là phân giác $\widehat{BAD}.$ Hãy chứng tỏ CA là phân giác $\widehat{BCD}.$

Lời giải

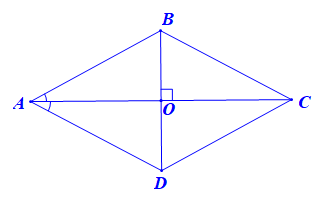
Vì ABCD là hình thoi nên AB // CD và AD // BC.

Do AB // CD nên $\widehat{BAC}=\widehat{DCA}$ (hai góc so le trong)

Do AD // BC nên $\widehat{CAD}=\widehat{ACB}$(hai góc so le trong)

Mà AC là tia phân giác của $\widehat{BAD}$ nên $\widehat{BAC}=\widehat{CAD}$

Suy ra $\widehat{DCA}=\widehat{ACB}$

Do đó CA là tia phân giác của $\widehat{BCD}.$

Vậy CA là tia phân giác của $\widehat{BCD}.$

Bài 7 trang 87 Sách bài tập Toán 7 Tập 1: Phát biểu giả thiết, kết luận, vẽ hình minh họa và chứng minh định lí: “Nếu một tứ giác có ba góc vuông thì góc còn lại cũng là góc vuông”.

Lời giải

Hình vẽ minh họa:

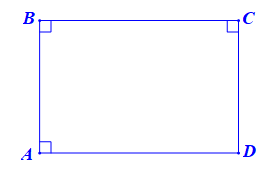
Viết giả thiết và kết luận bằng kí hiệu:

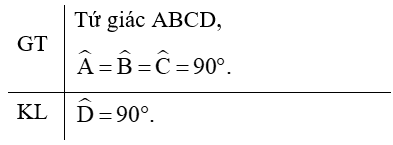
Chứng minh định lí:

Vì $\widehat{A}=\widehat{B}=90°$ nên AB ⊥ BC, AB ⊥ AD.

Do đó BC // AD (hai đường thẳng cùng vuông góc với một đường thẳng thứ ba thì song song)

Mà $\widehat{C}=90°$ nên BC ⊥ CD.

Ta có BC // AD và BC ⊥ CD.

Do đó AD ⊥ CD (một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó cũng vuông góc với đường thẳng còn lại).

Suy ra $\widehat{D}=90°.$

Vậy $\widehat{D}=90°.$

Giải SBT Toán 7 trang 88 Tập 1

Bài 8 trang 88 Sách bài tập Toán 7 Tập 1: Quan sát Hình 5, hãy chứng tỏ rằng xy // zt.

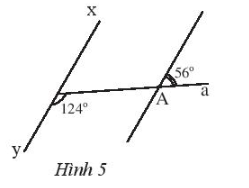
Lời giải   

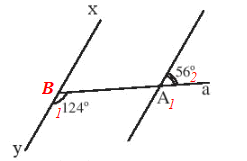
Đặt các góc A₁, A₂ và B₁ như hình vẽ.

Ta có ${\widehat{A}}_1$ và ${\widehat{A}}_2$ là hai góc kề bù nên:

${\widehat{A}}_1+{\widehat{A}}_2=180°.$

Suy ra ${\widehat{A}}_1=180°-{\widehat{A}}_2=180°-56°=124°.$

Do đó ${\widehat{A}}_1={\widehat{B}}_1=124°$

Mà ${\widehat{A}}_1$ và ${\widehat{B}}_1$ ở vị trí đồng vị

Nên xy // zt.

Bài 9 trang 88 Sách bài tập Toán 7 Tập 1: Quan sát Hình 6, hãy chứng tỏ rằng MN // EF.

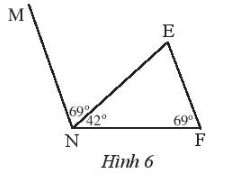
Lời giải   

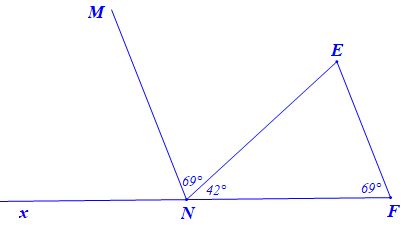
Vì $\widehat{MNE}$ và $\widehat{\text{ENF}}$ là hai góc kề nhau nên:

$\widehat{MNE}+\widehat{\text{ENF}}=\widehat{MNF}$

Suy ra $\widehat{MNF}=69°+42°=111°.$

Vẽ tia Nx là tia đối của tia NF.

Khi đó $\widehat{xNM}$ và $\widehat{MNF}$ là hai góc kề bù nên:

$\widehat{xNM}+\widehat{MNF}=180°$

Suy ra $\widehat{xNM}=180°-\widehat{MNF}$

Hay $\widehat{xNM}=180°-111°=69°$

Lại có $\widehat{NFE}=69°$ nên $\widehat{xNM}=\widehat{NFE}=69°$

Mà $\widehat{xNM}$ và $\widehat{NFE}$ là hai góc ở vị trí đồng vị.

Do đó MN // EF.

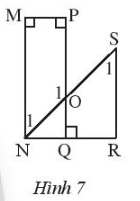
Bài 10 trang 88 Sách bài tập Toán 7 Tập 1: Quan sát Hình 7.

a) Chứng minh rằng MN // RS.

b) Cho ${\widehat{O}}_1=142°.$ Tính ${\widehat{N}}_1,{\widehat{S}}_1.$

Lời giải   

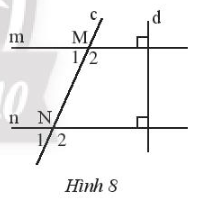
Bài 11 trang 88 Sách bài tập Toán 7 Tập 1: Quan sát Hình 8.

a) Chứng minh rằng m // n.

b) Cho ${\widehat{N}}_2=70°.$ Tính ${\widehat{M}}_1,{\widehat{M}}_2.$

Lời giải   

a) Ta có m ⊥ d và n ⊥ d.

Do đó m // n (hai đường thẳng cùng vuông góc với một đường thẳng thứ ba thì song song).

Vậy m // n.

b) Vì m // n nên ${\widehat{M}}_2={\widehat{N}}_2=70°$ (hai góc đồng vị).

Mà ${\widehat{M}}_2$ và ${\widehat{M}}_1$ là hai góc kề bù nên:

${\widehat{M}}_1+{\widehat{M}}_2=180°$

Suy ra ${\widehat{M}}_1=180°-{\widehat{M}}_2=180°-70°=110°.$

Vậy ${\widehat{M}}_2=70°$ và ${\widehat{M}}_1=110°.$

Bài 12 trang 88 Sách bài tập Toán 7 Tập 1: Hãy phát biểu phần kết luận còn thiếu của định lí sau:

a) Nếu một đường thẳng cắt hai đường thẳng song song thì tạo thành các cặp góc đồng vị .?.

b) Nếu hai đường thẳng cùng tạo với một đường thẳng các góc so le trong bằng nhau thì .?.

Lời giải

a) Nếu một đường thẳng cắt hai đường thẳng song song thì tạo thành các cặp góc đồng vị bằng nhau.

b) Nếu hai đường thẳng cùng tạo với một đường thẳng các góc so le trong bằng nhau thì hai đường thẳng đó song song với nhau.

Bài 13 trang 88 Sách bài tập Toán 7 Tập 1: Hãy phát biểu phần kết luận còn thiếu của định lí sau:

a) Hai góc cùng bù một góc thứ ba thì .?.

b) Hai đường phân giác của hai góc kề bù thì .?.

Lời giải   

a) Hai góc cùng bù một góc thứ ba thì bằng nhau.

b) Hai đường phân giác của hai góc kề bù thì vuông góc.

Giải SBT Toán 7 trang 89 Tập 1

Bài 14 trang 89 Sách bài tập Toán 7 Tập 1: Cho định lí: “Nếu một đường thẳng cắt hai đường thẳng sao cho có một cặp góc so le trong bằng nhau thì các cặp góc đồng vị có được cũng bằng nhau”.

a) Hãy vẽ hình minh họa định lí trên.

b) Viết giả thiết và kết luận của định lí.

c) Hãy chứng minh định lí trên.

Lời giải

a) Hình vẽ minh họa:

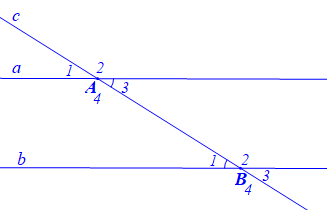
b) Viết giả thiết và kết luận bằng kí hiệu:

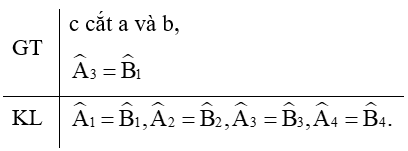
c) Chứng minh định lí:

• Vì ${\widehat{A}}_1$ và ${\widehat{A}}_3$ là hai góc đối đỉnh nên ${\widehat{A}}_1={\widehat{A}}_3.$

Mà ${\widehat{A}}_3={\widehat{B}}_1$ (giả thiết)

Suy ra ${\widehat{A}}_1={\widehat{B}}_1.$

Chứng minh tương tự ta có: ${\widehat{A}}_3={\widehat{B}}_3\left(={\widehat{B}}_1\right)$

• Lại có ${\widehat{A}}_1$ và ${\widehat{A}}_2$ là hai góc kề bù nên:

${\widehat{A}}_1+{\widehat{A}}_2=180°$

Suy ra ${\widehat{A}}_2=180°-{\widehat{A}}_1$      (1)

${\widehat{B}}_1$ và ${\widehat{B}}_2$ là hai góc kề bù nên:

${\widehat{B}}_1+{\widehat{B}}_2=180°$

Suy ra ${\widehat{B}}_2=180°-{\widehat{B}}_1$      (2)

Mà ${\widehat{A}}_1={\widehat{B}}_1$                      (3)

Từ (1), (2) và (3) suy ra ${\widehat{A}}_2={\widehat{B}}_2.$

Chứng minh tương tự ta cũng có ${\widehat{A}}_4={\widehat{B}}_4.$

Vậy định lí được chứng minh.

Xem thêm lời giải sách bài tập Toán lớp 7 Chân trời sáng tạo hay, chi tiết khác:

Bài 1: Thu tập và phân loại dữ liệu

Bài 2: Biểu đồ hình quạt tròn

Bài 3: Biểu đồ đoạn thẳng

Bài tập cuối chương 5

Bài 1: Tập hợp các số hữu tỉ

Xem thêm tài liệu Toán lớp 7 Chân trời sáng tạo hay, chi tiết khác:

Trắc nghiệm Ôn tập chương 4