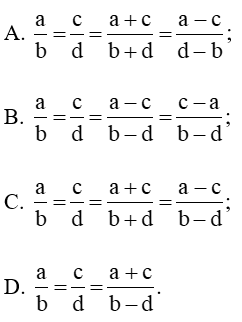Lý thuyết Tỉ lệ thức - Dãy tỉ số bằng nhau – Toán lớp 7 Chân trời sáng tạo

A. Lý thuyết Toán 7 Bài 1: Tỉ lệ thức - Dãy tỉ số bằng nhau - Chân trời sáng tạo

1. Tỉ lệ thức:

1.1. Khái niệm:

Với b, c ≠ 0 ta có tỉ lệ thức là đẳng thức của hai tỉ số: $\frac{a}{b}=\frac{c}{d}$

Tỉ lệ thức còn được viết là: a : b = c : d

Ví dụ:

$\frac{14}{7}=\frac{2}{1}$; $\frac{a}{0,2}=\frac{b}{2}$ là các tỉ lệ thức.

Hoặc có thể viết là: 14 : 7 = 2 : 1; a : 0,2 = b : 2.

1.2. Các tính chất:

* Tính chất 1: Nếu $\frac{a}{b}=\frac{c}{d}$ thì ad = bc. (b.d ≠ 0)

Ví dụ: Nếu ta có tỉ lệ thức $\frac{c}{2}=\frac{d}{3}$ thì 3.c = 2.d.

* Tính chất 2: Ngược lại so với tính chất 1 ta có:

Nếu ad = bc và a, b, c, d ≠ 0 thì ta có những tỉ lệ thức sau:

$\frac{a}{b}=\frac{c}{d}$; $\frac{a}{c}=\frac{b}{d}$; $\frac{d}{c}=\frac{b}{d}$ ; $\frac{d}{b}=\frac{c}{a}$ .

Ví dụ:Cho đẳng thức x.2 = 3.y.Với x, y ≠ 0 ta có các tỉ lệ thức sau:

$\frac{x}{3}=\frac{y}{2}$; $\frac{2}{3}=\frac{y}{x}$ ; $\frac{x}{y}=\frac{3}{2}$ ; $\frac{2}{y}=\frac{3}{x}$ .

2. Dãy tỉ số bằng nhau:

2.1. Khái niệm:

- Ta gọi các đẳng thức: $\frac{a}{b}=\frac{c}{d}=\frac{e}{f}$ là một dãy các tỉ số bằng nhau.

- Khi có dãy tỉ số bằng nhau $\frac{a}{b}=\frac{c}{d}=\frac{e}{f}$ , ta nói các số a, c, e tỉ lệ với các số b, d, f và có thể ghi là: a : c : e = b : d : f.

Ví dụ: Nếu ta có dãy tỉ số bằng nhau $\frac{a}{6}=\frac{b}{7}=\frac{c}{9}$ .

Ta nói các số a, b, c tỉ lệ với các số 6; 7; 9 và có thể ghi là: a : b : c = 6 : 7 : 8.

2.2. Các tính chất:

* Tính chất 1: $\frac{a}{b}=\frac{c}{d}=\frac{a+c}{b+d}=\frac{a-c}{b-d}$(các mẫu số phải khác 0).

Ví dụ:Nếu có tỉ lệ thức: $\frac{5,1}{3}=\frac{1,7}{1}$ .

Khi đó, ta có: $\frac{5,1}{3}=\frac{1,7}{1}=\frac{5,1-1,7}{3-1}=\frac{5,1+1,7}{3+1}$ .

* Tính chất 2: Tương tự với tỉ lệ thức, ta có tính chất sau của dãy tỉ số bằng nhau.

Từ dãy tỉ số bằng nhau $\frac{a}{b}=\frac{c}{d}=\frac{e}{f}$ ta viết được:

$\frac{a}{b}=\frac{c}{d}=\frac{e}{f}=\frac{a+c+e}{b+d+f}=\frac{a-c+e}{b-d+f}$ (các mẫu số phải khác 0).

Ví dụ:Cho dãy tỉ số bằng nhau: $\frac{x}{1}=\frac{y}{2}=\frac{z}{3}$ .

Khi đó, ta có: $\frac{x}{1}=\frac{y}{2}=\frac{z}{3}=\frac{x+y+z}{1+2+3}=\frac{x-y+z}{1-2+3}$ .

Bài tập Tỉ lệ thức - Dãy tỉ số bằng nhau

Bài 1: Lập tất cả các tỉ lệ thức có thể lập được từ các đẳng thức sau:

a) 4. 5,1 = 2. 10,2;

b) a . 3 = b . 6.

Hướng dẫn giải:

a) 4. 5,1 = 2. 10,2

Ta có các tỉ lệ thức sau:

$\frac{4}{2}=\frac{10,2}{5,1}$; $\frac{4}{10,2}=\frac{2}{5,1}$ ; $\frac{5,1}{10,2}=\frac{2}{4}$ ; $\frac{5,1}{2}=\frac{10,2}{4}$ .

b)a . 3 = b . 6

Ta có các tỉ lệ thức sau:

$\frac{a}{b}=\frac{6}{3}$; $\frac{a}{6}=\frac{b}{3}$ ; $\frac{3}{b}=\frac{6}{a}$ ; $\frac{3}{6}=\frac{b}{a}$ .

Bài 2. Tìm x, y, z biết:

a) $\frac{x}{2}=\frac{4}{5}$;

b) x + y = 10 và $\frac{x}{2}=\frac{y}{4}$;

c) x + y – z = 12 và $\frac{x}{2}=\frac{y}{4}=\frac{z}{3}$.

Hướng dẫn giải:

a)$\frac{x}{2}=\frac{4}{5}$

x . 5 = 4 . 2

5x = 8

$x=\frac{8}{5}$

Vậy $x=\frac{8}{5}$.

b) x + y = 10 và $\frac{x}{2}=\frac{y}{4}$

Áp dụng tính chất dãy tỉ số bằng nhau, ta có:

$\frac{x}{2}=\frac{y}{4}=\frac{x+y}{2+4}=\frac{10}{6}=\frac{5}{3}$.

Suy ra: $x=2.\frac{5}{3}=\frac{10}{3}$ ; $y=4.\frac{5}{3}=\frac{20}{3}$ .

Vậy $x=\frac{10}{3}$ ; $y=\frac{20}{3}$ .

c) x + y – z = 12 và $\frac{x}{2}=\frac{y}{4}=\frac{z}{3}$.

Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:

$\frac{x}{2}=\frac{y}{4}=\frac{z}{3}=\frac{x+y-z}{2+4-3}=\frac{12}{3}=4$

Suy ra x = 4.2 = 8; y = 4.4 = 16; z = 4.3 = 12.

Vậy x = 8; y = 16; z =12.

Bài 3. Ở một nhà máy sản xuất giày có ba nhóm làm việc A, B, C. Biết trong một ngày cả ba nhóm sản xuất được tổng 120 đôi giày. Biết số đôi giày làm được của ba nhóm A, B, C tỉ lệ lần lượt với các số 4 : 5 : 3. Hỏi mỗi nhóm sản xuất được bao nhiêu đôi giày trong một ngày?

Hướng dẫn giải:

Gọi x, y, z (đôi giày) lần lượt là số đôi giày sản xuất được của từng nhóm A, B, C sản xuất được trong một ngày (x, y, z $\in$ ℕ*).

Do số đôi giày làm được của ba nhóm A, B, C tỉ lệ lần lượt với các số 4 : 5 : 3 nên ta có: $\frac{x}{4}=\frac{y}{5}=\frac{x}{3}$

Mặt khác ta có tổng số đôi giày sản xuất được của cả ba nhóm trong một ngày là 120 đôi giày nên ta có: x + y + z = 120

Áp dụng tính chất dãy tỉ số bằng nhau, ta có:

$\frac{x}{4}=\frac{y}{5}=\frac{z}{3}=\frac{x+y+z}{4+5+3}$

Suy ra x = 4. 10 = 40; y = 5. 10 = 50; z = 3. 10 = 30 (thoả mãn).

Vậy số đôi giày sản xuất được của từng nhóm A, B, C sản xuất được trong một ngày lần lượt là: 40 đôi giày; 50 đôi giày; 30 đôi giày.

B. Trắc nghiệm Tỉ lệ thức - Dãy tỉ số bằng nhau (Chân trời sáng tạo 2023) có đáp án

Câu 1. Chọn câu sai. Nếu $\frac{a}{b}=\frac{c}{d}$ thì:

A. ad=bc;

B. $\frac{a}{c}=\frac{b}{d}$

C. $\frac{c}{a}=\frac{b}{d}$

D. $\frac{b}{a}=\frac{d}{c}$

Hiển thị đáp án

Đáp án đúng là: C

Ta có: $\frac{a}{b}=\frac{c}{d}$ suy ra $\frac{c}{a}=\frac{d}{b}\ne \frac{b}{d}$

Vậy chọn đáp án C.

Câu 2. Cho tỉ lệ thức $\frac{x}{3}=\frac{-2}{6}$. Giá trị của x là:

A. 1;

B. −1;

C. 6;

D. 3.

Hiển thị đáp án

Đáp án đúng là: B

Ta có $\frac{x}{3}=\frac{-2}{6}$

Suy ra

x . 6 = (−2) . 3

x . 6 = −6

x = −1

Vậy x = −1.

Vậy chọn đáp án B.

Câu 3. Cho tỉ lệ thức 5 : x = (−4) : 8. Giá trị của x là:

A. −10;

B. −4;

C. 10;

D. 4.

Hiển thị đáp án

Đáp án đúng là: A

Ta có 5 : x = (−4) : 8 nên $\frac{5}{x}=\frac{-4}{8}$

Suy ra

x . (−4) = 5 . 8

x . (−4) = 40

x = 40 : (−4)

x = −10

Vậy x = −10.

Vậy chọn đáp án A.

Câu 4. Các tỉ số nào sau đây lập thành một tỉ lệ thức?

A. $\frac{5}{7}:\frac{-3}{14}$ và $\frac{-1}{14}:\frac{3}{10}$

B. $\frac{2}{-5}$và $\frac{-6}{12}$

C.(−3) :7 và 6: (−7);

D. (-1):$\frac{2}{5}$ và $\frac{-5}{3}:\frac{4}{6}$

Hiển thị đáp án

Đáp án đúng là: D

Ta có:

$-1:\frac{2}{5}=(-1).\frac{5}{2}=\frac{-5}{2}$

Suy ra $\frac{-5}{3}:\frac{4}{6}=\frac{-5}{3}.\frac{6}{4}=\frac{-5}{2}$

Do đó, $(-1):\frac{2}{5}$ và $\frac{-5}{3}:\frac{4}{6}$ lập thành một tỉ lệ thức.

Vậy chọn đáp án D.

Câu 5. Chọn câu sai. Từ đẳng thức −2x = 3y, ta có tỉ lệ thức:

A. $\frac{x}{3}=\frac{y}{-2}$

B. $\frac{x}{y}=\frac{3}{-2}$

C. $\frac{x}{-2}=\frac{y}{3}$

D. $\frac{3}{x}=\frac{2}{-y}$

Hiển thị đáp án

Đáp án đúng là: C

Theo bài ra −2x = 3y. Suy ra $\frac{x}{y}=\frac{3}{-2}$(tính chất tỉ lệ thức)

Nếu $\frac{x}{-2}=\frac{y}{3}$ thì $\frac{x}{y}=\frac{-2}{3}\ne \frac{3}{-2}$

Do đó $\frac{x}{-2}=\frac{y}{3}$ là sai.

Vậy chọn đáp án C.

Câu 6. Chọn câu đúng. Chọn dãy tỉ số bằng nhau.

Hiển thị đáp án

Đáp án đúng là: C.

Áp dụng tính chất dãy tỉ số bằng nhau, ta có:

$\frac{a}{b}=\frac{c}{d}=\frac{a+c}{b+d}=\frac{a-c}{b-d}$

Vậy chọn đáp án C.

Câu 7. Tìm hai số x; y biết $\frac{x}{3}=\frac{y}{5}$ và x + y = −24.

A. x = −9; y = −15;

B. x = 9; y = 15;

C. x = −9; y = 15;

D. x = 9; y = 15.

Hiển thị đáp án

Đáp án đúng là: A

Áp dụng tính chất dãy tỉ số bằng nhau, ta có:

$\frac{x}{3}=\frac{y}{5}=\frac{x+y}{3+5}=\frac{-24}{8}=-3$

Suy ra x = (−3) . 3 = −9; y = (−3) . 5 = −15.

Vậy chọn đáp án A.

Câu 8. Tìm hai số x và y biết $\frac{x}{4}=\frac{y}{7}$ và x − y = −6.

A. x = 8; y = 14;

B. x = −8; y = 14;

C. x = 8; y = −14;

D. x = −8; y = −14.

Hiển thị đáp án

Đáp án đúng là: A

Áp dụng tính chất dãy tỉ số bằng nhau, ta có:

$\frac{x}{4}=\frac{y}{7}=\frac{x-y}{4-7}=\frac{-6}{-3}=2$

Suy ra x = 2 . 4 = 8; y = 2 . 7 = 14.

Vậy chọn đáp án A.

Câu 9. Cho 2x = 3y và y − x = −2. Tìm x và y.

A. x = 4; y = 6;

B. x = 6; y = 4;

C. x = −4; y = −6;

D. x = −6; y = −4.

Hiển thị đáp án

Đáp án đúng là: B

Theo tính chất tỉ lệ thức, ta có 2x = 3y nên $\frac{x}{3}=\frac{y}{2}$

Áp dụng tính chất dãy tỉ số bằng nhau, ta có:

$\frac{x}{3}=\frac{y}{2}=\frac{y-x}{2-3}=\frac{-2}{-1}=2$

Suy rax = 2 . 3 = 6; y = 2 . 2 = 4.

Vậy chọn đáp án B.

Câu 10. Cho $\frac{x}{y}=\frac{2}{-7}$ và 2x + y = 9. Tìm x và y.

A. x = 21; y = 6;

B. x = −6; y = 21;

C. x = 6; y = −21;

D. x = 6; y = 21.

Hiển thị đáp án

Đáp án đúng là: B

Ta có: $\frac{x}{y}=\frac{2}{-7}$ suy ra $\frac{x}{2}=\frac{y}{-7}$

Áp dụng tính chất dãy tỉ số bằng nhau ta có:

$\frac{x}{2}=\frac{y}{-7}=\frac{2x+y}{2.2-7}=\frac{9}{-3}=-3$

Suy ra x = (−3).2 = −6; y = (−3).(−7) = 21.

Vậy chọn đáp án B.

Xem thêm tóm tắt lý thuyết Toán lớp 7 sách Chân trời sáng tạo hay, chi tiết khác:

Lý thuyết Bài 2: Đại lượng tỉ lệ thuận

Lý thuyết Bài 3: Đại lượng tỉ lệ nghịch

Lý thuyết Ôn tập Chương 6

Lý thuyết Bài 1: Biểu thức số, biểu thức đại số

Lý thuyết Bài 2: Đa thức một biến