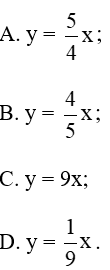Lý thuyết Đại lượng tỉ lệ thuận – Toán lớp 7 Chân trời sáng tạo

A. Lý thuyết Toán 7 Bài 2: Đại lượng tỉ lệ thuận - Chân trời sáng tạo

1. Khái niệm:

Cho k là hằng số khác 0, ta nói đại lượng y tỉ lệ thuận với đại lượng x theo hệ số tỉ lệ k nếu y liên hệ với x theo công thức: y = kx.

Từ y = kx (k ≠ 0) ta suy ra $x=\frac{1}{k}y$ . Vậy nếu y tỉ lệ thuận với x theo hệ số tỉ lệ k thì x cũng tỉ lệ thuận với y theo hệ số tỉ lệ $\frac{1}{k}$ và ta nói hai đại lưỡng x, y tỉ lệ thuận với nhau.

Ví dụ:

- Nếu y = 2x thì ta nói đại lượng y tỉ lệ thuận với đại lượng x theo hệ số tỉ lệ là 2.

- Nếu $b=\frac{1}{2}a$ thì ta nói đại lượng b tỉ lệ thuận với đại lượng a theo hệ số tỉ lệ $\frac{1}{2}$ .

2. Tính chất của các đại lượng tỉ lệ thuận:

Nếu hai đại lượng tỉ lệ thuận với nhau thì:

- Tỉ số hai giá trị tương ứng của chúng luôn không đổi:

$\frac{y_1}{x_1}=\frac{y_2}{x_2}=\frac{y_3}{x_3}=\mathrm{...}$

- Tỉ số hai giá trị tùy ý của đại lượng này bằng tỉ số hai giá trị tương ứng của đại lượng kia:

$\frac{x_1}{x_2}=\frac{y_1}{y_2}$; $\frac{x_1}{x_3}=\frac{y_1}{y_3}$ ;...

Ví dụ: Cho biết giá trị tương ứng của các đại lượng y và x tỉ lệ thuận với nhau trong bảng sau:

x	x1 = 2	x2 = 3	x3 = 5	x4 = 7
y	y1 = 4	y2 = 6	y3 = 10	y4 = 14

Khi đó, ta có:

∙ $\frac{y_1}{x_1}=\frac{y_2}{x_2}=\frac{y_3}{x_3}=\frac{y_4}{x_4}=2$;

∙ $\frac{x_1}{x_2}=\frac{y_1}{y_2}=\frac{2}{3}$ ; $\frac{x_3}{x_4}=\frac{y_3}{y_4}=\frac{5}{7}$ ;…

Bài tập Đại lượng tỉ lệ thuận

Bài 1. Cho hai đại lượng x và y tỉ lệ thuận với nhau. Biết rằng khi x = 3 thì y = 9.

a) Tìm hệ số tỉ lệ k của x đối với y.

b) Tìm y khi x = 2.

Hướng dẫn giải:

a) Do x tỉ lệ thuận với y theo hệ số k, nên ta có x = k.y.

Suy ra: $k=\frac{x}{y}=\frac{3}{9}=\frac{1}{3}$ .

b) Theo câu a, ta có: y = 3x.

Suy ra y = 3.2 = 6.

Vậy y = 6 khi x = 2.

Bài 2. Cho m và n là hai đại lượng tỉ lệ thuận với nhau. Hãy viết công thức tính m theo n và tính các giá trị chưa biết và điền vào bảng sau:

m	2	−4	?	−5
n	10	?	30	?

Hướng dẫn giải:

Ta có: m = 2 và n = 10. Mặt khác m, n là hai đại lượng tỉ lệ thuận với nhau theo tỉ số k, nên ta có: n = k. m.

Suy ra $k=\frac{n}{m}=\frac{10}{2}=5$ .

Từ đó ta có n = 5m. Khi đó, ta có:

Với m = −4 thì n = 5.(−4) = 20;

Với n = 30 thì m = 30 : 5 = 6;

Với m = −5 thì n = 5.(−5) = 25.

Vậy ta có bảng sau:

m	2	−4	6	−5
n	10	−20	30	−25

Bài 3. Nhà bác An và bác Bích cùng nhau nuôi lợn, bác An nuôi 1 con, bác Bích nuôi 2 con. Sau khi bán hết số lợn thì thu được tổng 7,5 triệu đồng, hai người quyết định chia số tiền tỉ lệ với số con lợn mỗi người đã nuôi. Tính số tiền mỗi người nhận được?

Hướng dẫn giải:

Gọi x và y (triệu đồng) lần lượt là số tiền được chia của bác An và bác Bích (0 < x, y < 7,5).

Do số tiền và số con lợn của nhà bác An và bác Bích là hai đại lượng tỉ lệ thuận với nhau, nên ta có: $\frac{x}{1}=\frac{y}{2}$ .

Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:

$\frac{x}{1}=\frac{y}{2}=\frac{x+y}{1+2}=\frac{7,5}{3}=2,5$

Suy ra: x = 2,5.1 = 2,5; y = 2,5.2 = 5 (thỏa mãn)

Vậy bác An nhận được 2,5 triệu đồng; bác Bích nhận được 5 triệu đồng.

B. Trắc nghiệm Đại lượng tỉ lệ thuận (Chân trời sáng tạo 2023) có đáp án

Câu 1. Cho biết x và y là hai đại lượng tỉ lệ thuận theo hệ số −6. Hãy biểu diễn y theo x.

A. y = 6x;

B. y = $\frac{1}{6}x$

C. y = −6x;

D. y = $\frac{-1}{6}$x.

Hiển thị đáp án

Đáp án đúng: D

Vì x tỉ lệ thuận với y theo hệ số tỉ lệ là −6 nên ta có x = −6y.

Suy ra $y=\frac{x}{-6}=\frac{-1}{6}x$

Vậy biểu diễn y theo x là $y=\frac{-1}{6}x$.

Chọn đáp án D.

Câu 2. Cho đại lượng y tỉ lệ thuận với đại lượng x theo hệ số k (k ≠ 0). Gọi x₁; x₂ là các giá trị của đại lượng x và y₁; y₂ là các giá trị của đại lượng y tương ứng, biết x₁ = 2,5 thì y₁ = −0,5. Hãy tính x₂ khi y₂ = 5.

A. x₂ = −0,25;

B. x₂ = 5;

C. x₂ = −25;

D. x₂ = 10.

Hiển thị đáp án

Đáp án đúng: C

Vì y tỉ lệ thuận với đại lượng x theo hệ số k nên ta có $\frac{x_1}{x_2}=\frac{y_1}{y_2}$

Thay số $\frac{2,5}{x_2}=\frac{-0,5}{5}$

Suy ra $x_2=\frac{2,5.5}{-0,5}=-25$

Vậy x₂= −25.

Chọn đáp án C.

Câu 3. Cho biết x và y là hai đại lượng tỉ lệ thuận, khi x = 5 thì y = 25. Hệ số tỉ lệ k của y đối với x là:

A. 5;

B. 125;

C. $\frac{1}{5}$;

D. 20.

Hiển thị đáp án

Đáp án đúng là: A

Vì y tỉ lệ thuận với x theo hệ số tỉ lệ k nên y = kx.

Suy ra $k=\frac{y}{x}=\frac{25}{5}=5$

Vậy hệ số tỉ lệ k của y đối với x là 5.

Chọn đáp án A.

Câu 4. Cho biết x và y là hai đại lượng tỉ lệ thuận, khi x = 5 thì y = 25. Hệ số tỉ lệ k của x đối với y là:

A. 5;

B. 20;

C. 125;

D. $\frac{1}{5}$.

Hiển thị đáp án

Đáp án đúng là: D

Vì x tỉ lệ thuận với y theo hệ số tỉ lệ k nên ta có: x = ky.

Suy ra $k=\frac{x}{y}=\frac{5}{25}=\frac{1}{5}$

Vậy số tỉ lệ k = $\frac{1}{5}$

Vậy chọn đáp án D.

Câu 5. Một công nhân làm được 20 sản phẩm trong 40 phút. Trong 60 phút người đó làm được bao nhiêu sản phẩm cùng loại?

A. 10 sản phẩm;

B. 30 sản phẩm;

C. 15 sản phẩm;

D. 35 sản phẩm.

Hiển thị đáp án

Đáp án đúng là: B

Gọi x (sản phẩm) là số sản phẩm người đó làm trong 60 phút (x $\in$ ℕ^*).

Vì số sản phẩm tỉ lệ thuận với thời gian làm sản phẩm nên ta có:

$\frac{x}{20}$ = $\frac{60}{40}$

Suy ra x = $\frac{60}{40}.20=30$ (thỏa mãn điều kiện).

Vậy trong 60 phút người đó làm được 30 sản phẩm.

Chọn đáp án B.

Câu 6. Một hình chữ nhật có hai cạnh tỉ lệ lần lượt với 9 và 6, chu vi là 300 cm. Chiều dài và chiều rộng của hình chữ nhật lần lượt là:

A. 40 cm và 60 cm;

B. 90 cm và 60 cm;

C. 40 cm và 90 cm;

D. 60 cm và 40 cm.

Hiển thị đáp án

Đáp án đúng là: B

Gọi x, y (m) lần lượt là chiều dài và chiều rộng của hình chữ nhật (0 < x, y < 150)

Nửa chu vi hình chữ nhật là:

x + y = 300 : 2 = 150 (m).

Hai cạnh của hình chữ nhật tỉ lệ với 9 và 6. Tức là chiều dài và chiều rộng của hình chữ nhật tỉ lệ với 9 và 6 nên ta có: $\frac{x}{9}=\frac{y}{6}$

Áp dụng tính chất dãy tỉ số bằng nhau ta có:

$\frac{x}{9}=\frac{y}{6}=\frac{x+y}{9+6}=\frac{150}{15}=10$

Suy ra x = 9 . 10 = 90; y = 6 . 10 = 60 (thỏa mãn điều kiện)

Vậy hình chữ nhật có chiều dài là 90 m, chiều rộng là 60 m.

Chọn đáp án B.

Câu 7. Cho hai đại lượng x và y tỉ lệ thuận với nhau và khi x = 48 thì y = 12. Hãy biểu diễn y theo x.

A. y = 4x;

B. y = 36x;

C. y = 60x;

D. y = $\frac{1}{4}$x.

Hiển thị đáp án

Đáp án đúng là: D

Giả sử y tỉ lệ thuận với x theo hệ số tỉ lệ k.

Ta có: y = kx.

Suy ra k = $\frac{y}{x}=\frac{12}{48}=\frac{1}{4}$

Vậy biểu diễn y theo x là y = $\frac{1}{4}x$

Chọn đáp án D.

Câu 8. Cho y tỉ lệ thuận với x. Gọi x₁; x₂ lần lượt là các giá trị tương ứng của x và y₁; y₂ lần lượt là các giá trị tương ứng của y khi x₁ = −3 thì y₁ = 9. Vậy khi x₂ = 1 thì y₂ có giá trị là:

A. y = −3;

B. y = 27;

C. y = 3;

D. y = −27.

Hiển thị đáp án

Đáp án đúng là: A

Ta có k = $\frac{y_1}{x_1}=\frac{y_2}{x_2}$

Suy ra: $\frac{9}{-3}=\frac{y_2}{1}$

Do đó $y_2=\frac{9.1}{-3}=-3$

Vậy khi x₂ = 1 thì y₂ = −3.

Chọn đáp án A.

Câu 9. Cứ 100 kg thóc thì thu được 70 kg gạo. Hỏi để thu được 140 kg gạo thì cần bao nhiêu tạ thóc?

A. 200 tạ;

B. 2 tạ;

C. 98 tạ;

D. 50 tạ.

Hiển thị đáp án

Đáp án đúng là: B

Gọi x (kg) là số kg thóc cần để thu được 140 kg gạo (x > 0)

Vì số gạo và số thóc tỉ lệ thuận với nhau nên ta có:

$\frac{x}{140}$ = $\frac{100}{70}$

Suy ra: x = $\frac{100}{70}$.140 = 200 (thỏa mãn điều kiện).

Nên x = 200 (kg)

Đổi 200 kg = 2 tạ.

Vậy để thu được 140 kg gạo thì cần 2 tạ thóc.

Chọn đáp án B.

Câu 10. Giả sử x và y là hai đại lượng tỉ lệ thuận x₁, x₂ là hai giá trị khác nhau của x có tổng bằng 4 và y₁, y₂ là hai giá trị của y có tổng bằng 5. Biểu diễn y theo x là:

Hiển thị đáp án

Đáp án đúng là: A

Áp dụng tính chất dãy tỉ số bằng nhau, ta có:

$\frac{x}{y}=\frac{x_1+x_2}{y_1+y_2}=\frac{4}{5}$

Suy ra y = $\frac{5}{4}$x

Vậy biểu diễn y theo x là y = $\frac{5}{4}$x

Chọn đáp án A.

Xem thêm tóm tắt lý thuyết Toán lớp 7 sách Chân trời sáng tạo hay, chi tiết khác:

Lý thuyết Bài 1: Tỉ lệ thức - Dãy tỉ số bằng nhau

Lý thuyết Bài 3: Đại lượng tỉ lệ nghịch

Lý thuyết Ôn tập Chương 6

Lý thuyết Bài 1: Biểu thức số, biểu thức đại số

Lý thuyết Bài 2: Đa thức một biến