15 câu hỏi trắc nghiệm thuộc Trắc nghiệm Cung và góc lượng giác có đáp án (Thông hiểu)

Câu 1:

14/07/2024

Tìm mệnh đề đúng trong các mệnh đề sau:

A. Số đo của một cung lượng giác luôn là một số không âm

B. Số đo của một cung lượng giác luôn không vượt quá 2π

C. Số đo của một cung lượng giác luôn là một số thực thuộc đoạn [0; 2π]

D. Số đo của một cung lượng giác là một số thực

Xem đáp án

Đáp án D

Nếu một cung lượng giác có số đo $a °$ (hay α rad) thì mọi cung lượng giác có cùng điểm đầu và điểm cuối với cung lượng giác đã cho đều có số đo dạng $a ° + k 360 °$ hoặc α + k2π.

Do đó số đo của một cung lượng giác có thể âm, có thể dương, có thể nằm trong đoạn [0; 2π] cũng có thể không.

Nói chung số đo của một cung lượng giác là một số thực

Câu 2:

19/07/2024

Cung lượng giác nào sau đây có mút trùng với B hoặc B′

A. $α = \frac{π}{2} + k 2 π$

B. $α = - \frac{π}{2} + k 2 π$

C. $a = 90 ° + k 360 °$

D. $a = - 90 ° + k 180 °$

Xem đáp án

Đáp án D

Cung lượng giác có đầu mút trùng với B hoặc B′ nghĩa là có hai điểm biểu diễn, do đó số đo có dạng $α + \frac{k 2 π}{2} = α + kπ$ hoặc $a + 180 °$ . Loại A, B, C.

Ngoài ra số đo cung AB′ bằng $- 90 °$ nên ta được $a = - 90 ° + k 180 °$

Câu 3:

18/07/2024

Cho bốn cung lượng giác (trên một đường tròn định hướng) $α = - \frac{5 π}{6}; β = \frac{π}{3}; γ = \frac{25 π}{3}; δ = \frac{19 π}{6}$ có cùng điểm đầu. Các cung nào có điểm cuối trùng nhau:

A. α và β; γ và δ

B. β và γ; α và δ

C. α, β, γ

D. β, γ, δ

Xem đáp án

Đáp án B

Ta có δ – α = 4π ⇒ hai cung α và δ có điểm cuối trùng nhau.

Và γ – β = 8π ⇒ hai cung β và γ có điểm cuối trùng nhau

Câu 4:

23/07/2024

Trên đường tròn lượng giác gốc A cho các cung có số đo:

(I). $\frac{π}{4}$

(II). $- \frac{7 π}{4}$

(III). $\frac{13 π}{4}$

(IV). $- \frac{5 π}{4}$

Hỏi các cung nào có điểm cuối trùng nhau?

A. Chỉ (I) và (II)

B. Chỉ (I), (II) và (III)

C. Chỉ (II), (III) và (IV)

D. Chỉ (I), (II) và (IV)

Xem đáp án

Đáp án A

Ta có:

$- \frac{7 π}{4} = \frac{π}{4} - 2 π; \frac{13 π}{4} = \frac{5 π}{4} + 2 π; - \frac{5 π}{4} = \frac{3 π}{4} - 2 π$

Suy ra chỉ có hai cung $\frac{π}{4}$ và $- \frac{7 π}{4}$ có điểm cuối trùng nhau

Câu 5:

09/11/2024

Các cặp góc lượng giác sau ở trên cùng một đường tròn đơn vị, cùng tia đầu và tia cuối. Hãy nêu kết quả SAI trong các kết quả sau đây:

A. $\frac{π}{3} v à - \frac{35 π}{3}$

B. $\frac{π}{10} v à \frac{152 π}{5}$

C. $- \frac{π}{3} và \frac{155 π}{3}$

D. $\frac{π}{7} v à \frac{281 π}{7}$

Xem đáp án

Đáp án đúng là B

Lời giải

Cặp góc lượng giác a và b ở trên cùng một đường tròn đơn vị, cùng tia đầu và tia cuối.

Khi đó a = b + k2π, k ∈ Z hay $k = \frac{a - b}{2 π}$

Dễ thấy, ở đáp án B vì $k = \frac{\frac{π}{10} - \frac{152 π}{5}}{2 π} = - \frac{303}{20} \notin Z$

*Phương pháp giải:

- Sử dụng tính chất:

Hai góc lượng giác có cùng tia đầu và tia cuối thì hơn kém nhau một bội chẵn lần của $π$ hay $a - b = k 2 π (k \in Z)$

Góc lượng giác và cung lượng giác

*Lý thuyết:

I. Góc lượng giác

1. Góc hình học và số đo của chúng

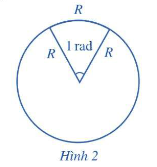
*Nhận xét:

- Đơn vị đo góc: độ hoặc radian (rad).

- Ta có: $180^{o} = π$ rad, do đó 1 rad $= {(\frac{180}{π})}^{o}$ , $1^{o} = (\frac{π}{180})$ rad.

- Người ta thường không viết chữ radian hay rad sau số đo góc.

VD: $\frac{π}{2}$ rad cũng được viết là $\frac{π}{2}$ .

2. Góc lượng giác và số đo của chúng

a, Khái niệm

- Cho 2 tia Ou, Ov. Nếu tia Om quay chỉ theo chiều dương (hay chỉ theo chiều âm) xuất phát từ Ou đến trùng với tia Ov thì ta nói: Tia Om quét một góc lượng giác với tia đầu Ou và tia cuối Ov.

Kí hiệu: (Ou, Ov).

- Mỗi góc lượng giác được xác định bởi tia đầu Ou, tia cuối Ov và số đo của góc đó.

b, Tính chất

- Cho hai góc lượng giác = và (O’u’,O’v’) có tia đầu trùng nhau $(O u \equiv O^{'} u^{'})$ , tia cuối trùng nhau $(O v \equiv O^{'} v^{'})$ .

Khi đó, nếu sử dụng đợn vị đo là độ thì ta có:

$(O u, O v) = (O^{'} u^{'}, O^{'} v^{'}) + k 360^{o}, k \in Z .$

Nếu sử dụng đơn vị đo là radian thì:

$(O u, O v) = (O^{'} u^{'}, O^{'} v^{'}) + k 2 π, k \in Z .$

* Hệ thức Chasles

Với 3 tia Ou, Ov, Ow bất kì ta có:

(Ou,Ov) + (Ov, Ow) = (Ou,Ow) $+ k 2 π, k \in Z .$

II. Giá trị lượng giác của góc lượng giác

1. Đường tròn lượng giác

Trong mặt phẳng toa độ đã được định hướng Oxy, lấy điểm A(1;0). Đường tròn tâm O, bán kính OA = 1 được gọi là đường tròn lượng giác (hay đường tròn đơn vị) gốc A.

2. Giá trị lượng giác của góc lượng giác

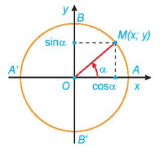
- Trục tung là trục sin, trục hoành là trục côsin.

- Điểm M(x;y) nằm trên đường tròn như hình vẽ. Khi đó:

$x =$ cos $α$ , $y =$ sin $α$ .

tan $α$ $= \frac{\sin α}{\cos α} = \frac{y}{x} (x \neq 0)$

$\cot α = \frac{\cos α}{\sin α} = \frac{x}{y} (y \neq 0)$

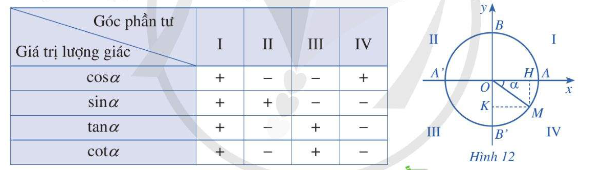
* Dấu của các giá trị lượng giác của góc $α$

Xem thêm

Góc và cung lượng giác và cách giải bài tập (2024) chi tiết nhất

TOP 40 câu Trắc nghiệm Tỉ số lượng giác của góc nhọn và Bảng lượng giác (có đáp án 2024) - Toán

Câu 6:

21/07/2024

Chọn điểm A (1; 0) làm điểm đầu của cung lượng giác trên đường tròn lượng giác. Tìm điểm cuối M của cung lượng giác có số đo $\frac{25 π}{4}$

A. M là điểm chính giữa của cung phần tư thứ I

B. M là điểm chính giữa của cung phần tư thứ II

C. M là điểm chính giữa của cung phần tư thứ III

D. M là điểm chính giữa của cung phần tư thứ IV

Xem đáp án

Đáp án A

Theo giả thiết ta có số đo cung AM bằng $\frac{25 π}{4} = \frac{π}{4} + 6 π$ , suy ra điểm M trùng với điểm cuối của góc lượng giác $\frac{π}{4}$ hay nó là điểm chính giữa của cung phần tư thứ I

Câu 7:

18/07/2024

Một đường tròn có đường kính bằng 20cm. Tính độ dài của cung trên đường tròn có số đo $35 °$ (lấy 2 chữ số thập phân)

A. 6,01cm

B. 6,11cm

C. 6,21cm

D. 6,31cm

Xem đáp án

Đáp án B

Cung có số đo $35 °$ thì số đo radian là $α = \frac{a π}{180} = \frac{35 π}{180} = \frac{7 π}{36}$

Bán kính đường tròn $R = \frac{20}{2} = 10 c m$

Suy ra $l = α R = \frac{7 π}{36} .10 \approx 6, 11 c m$

Câu 8:

23/07/2024

Tìm số đo cung có độ dài của cung bằng $\frac{40}{3}$ cm trên đường tròn bán kính 20 cm

A. 1,5rad

B. 0,67rad

C. $80 °$

D. $88 °$

Xem đáp án

Đáp án B

Ta có $l = α R \Leftrightarrow α = \frac{l}{R} = \frac{\frac{40}{3}}{20} = \frac{2}{3} \approx 0, 67 r a d$

Câu 9:

23/10/2024

Trên đường tròn bán kính R, cung tròn có độ dài bằng $\frac{1}{6}$ độ dài nửa đường tròn thì có số đo (tính bằng radian) là:

A. $\frac{π}{2}$

B. $\frac{π}{3}$

C. $\frac{π}{4}$

D. $\frac{π}{6}$

Xem đáp án

Đáp án đúng: D

*Phương pháp giải:

- do cung tròn có độ dài bằng 1/6 độ dài nửa đường tròn. vậy độ dài cung = 1/6 . độ dài nửa đường tròn là pi.R

- áp dụng công thức để tính ra số đo của cung

*Lời giải:

Ta có $l = α R \Leftrightarrow α = \frac{l}{R} = \frac{\frac{1}{6} π R}{R} = \frac{π}{6}$

* Lý thuyết và các dạng bài về giá trị lượng giác của một cung:

a) Cho đường tròn (O; R) như hình sau:

Một cung của đường tròn bán kính R và có số đo α rad có độ dài l = Rα,

trong đó: + R là bán kính đường tròn;

+ α là số đo bằng rad của cung tròn;

+ l là độ dài cung tròn.

Một cung của đường tròn bán kính R và có số đo a° có độ dài l = $\frac{πRa}{180}$ ,

trong đó: + R là bán kính đường tròn;

+ a là số đo bằng độ của cung tròn;

+ l là độ dài cung tròn.

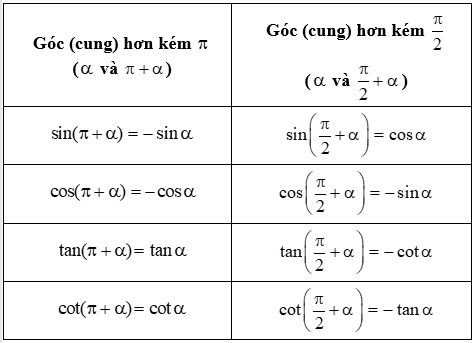
Các công thức lượng giác cơ bản:

CÁC DẠNG BÀI:

Dạng 1: Tính các giá trị lượng giác còn lại khi đã cho trước một giá trị

Phương pháp giải:

Để làm dạng bài tập này, ta sử dụng các công thức lượng giác cơ bản, giá trị lượng giác của các cung có liên quan đặc biệt và dấu của các giá trị lượng giác.

Dạng 2: Chứng minh một đẳng thức giữa các giá trị lượng giác

Phương pháp giải:

Sử dụng công thức lượng giác và các giá trị lượng giác của các góc liên quan đặc biệt để thực hiện phép biến đổi.

Ta lựa chọn một trong các cách biến đổi sau:

* Cách 1: Biến đổi một vế thành vế còn lại (vế trái thành vế phải hoặc vế phải thành vế trái)

* Cách 2: Biến đổi đẳng thức cần chứng minh về một đẳng thức đã biết là luôn đúng.

* Cách 3: Biến đổi một đẳng thức đã biết là luôn đúng thành đẳng thức cần chứng minh.

Dạng 3: Rút gọn biểu thức lượng giác

Phương pháp giải:

Để giải dạng bài này, ta sẽ áp dụng các công thức lượng giác cơ bản và các giá trị lượng giác của các góc có mối liên hệ đặc biệt để đưa biểu thức ban đầu trở nên đơn giản, ngắn gọn hơn.

Xem thêm các bài viết liên quan hay, chi tiết:

Lý thuyết góc và cung lượng giác và cách giải bài tập chi tiết nhất

Góc và cung lượng giác và cách giải bài tập (2024) chi tiết nhất

Trắc nghiệm Cung và góc lượng giác có đáp án – Toán lớp 10

Câu 10:

23/07/2024

Một cung có độ dài 10cm, có số đo bằng radian là 2,5 thì đường tròn của cung đó có bán kính là:

A. 2,5cm

B. 3,5cm

C. 4cm

D. 4,5cm

Xem đáp án

Đáp án C

Ta có: $l = α R \Leftrightarrow R = \frac{l}{α} = \frac{10}{2, 5} = 4$

Câu 11:

21/07/2024

Cho góc lượng giác $(Ox, Oy) = 22 ° 30' + k 360 °$ . Với giá trị k bằng bao nhiêu thì góc $(Ox, Oy) = 1822 ° 30'$ ?

A. k ∈ ∅

B. k = 3

C. k = −5

D. k = 5

Xem đáp án

Đáp án D

$(Ox, Oy) = 1822 ° 30' \Leftrightarrow 22 ° 30' + k 360 ° = 1822 ° 30' \Leftrightarrow k = 5$

Câu 12:

23/07/2024

Cho góc lượng giác (OA, OB) có số đo bằng $\frac{π}{2}$ . Hỏi trong các số sau, số nào là số đo của một góc lượng giác có cùng tia đầu, tia cuối với góc lượng giác (OA, OB)?

A. $\frac{6 π}{5}$

B. $- \frac{11 π}{5}$

C. $\frac{9 π}{5}$

D. $\frac{31 π}{5}$

Xem đáp án

Đáp án D

$\frac{6 π}{5} = \frac{π}{5} + π$ nên loại A

$- \frac{11 π}{5} = - \frac{π}{5} - 2 π$ nên loại B

$\frac{9 π}{5} = \frac{4 π}{5} + π$ nên loại C

$\frac{31 π}{5} = \frac{π}{5} + 6 π$ nên chọn D

Câu 13:

23/07/2024

Nếu góc lượng giác có tia đầu Ox và tia cuối Oz thỏa mãn sd (Ox, Oz) = $- \frac{63 π}{2}$ thì hai tia Ox và Oz

A. Trùng nhau

B. Vuông góc

C. Tạo với nhau một góc bằng $\frac{3 π}{4}$

D. Đối nhau

Xem đáp án

Đáp án B

Ta có $s d (O x, O z) = - \frac{63 π}{2} = \frac{π}{2} - \frac{64 π}{2} = \frac{π}{2} - 32 π$ nên hai tia Ox và Oz vuông góc

Câu 14:

21/07/2024

Cung α có điểm đầu là A và điểm cuối là M trên đường tròn đơn vị như hình vẽ thì số đo của α là:

A. $\frac{3 π}{4} + k π$

B. $- \frac{3 π}{4} + k π$

C. $\frac{3 π}{4} + k 2 π$

D. $- \frac{3 π}{4} + k 2 π$

Xem đáp án

Đáp án D

Cung α có mút đầu là A và mút cuối là M theo chiều dương có số đo là $\frac{5 π}{4} + k 2 π$ nên loại A, C.

Cung α có mút đầu là A và mút cuối là M theo chiều âm có số đo là $- \frac{3 π}{4}$ và chỉ có duy nhất một điểm M trên đường tròn lượng giác nên loại B

Câu 15:

20/10/2024

Cho góc lượng giác $α = \frac{π}{2} + k 2 π, k \in ℤ$ . Tìm k để 10π < α < 11π.

A. k = 4

B. k = 5

C. k = 6

D. k = 7

Xem đáp án

Đáp án đúng là B

*Phương pháp giải

Thay giá trị của $α$ vào khoảng giá trị để tìm ra k

*Lời giải

Ta có

$10 π < α < 11 π \Leftrightarrow 10 π < \frac{π}{2} + k 2 π < 11 π \Leftrightarrow \frac{19 π}{2} < k 2 π < \frac{21 π}{2} \Leftrightarrow k = 5$

Xem thêm các bài viết liên quan hay, chi tiết:

Tổng hợp bảng giá trị lượng giác

Trắc nghiệm Giá trị lượng giác của một góc bất kì từ 0 độ đến 180 độ có đáp án

Lớp 1 - Cánh diều

Tiếng Anh 1

Toán lớp 1

Tiếng Việt lớp 1

Lớp 1 - Chân trời sáng tạo

Tiếng Anh 1

Toán lớp 1

Tiếng Việt lớp 1

Lớp 1 - Kết nối tri thức

Tiếng Anh 1

Toán lớp 1

Tiếng Việt lớp 1

Tiện ích

Đọc sách online

Bộ đề ôn hè lớp 1 lên lớp 2

Giáo án lớp 1

Lớp 2 - Kết nối tri thức

Toán lớp 2

Tiếng Việt lớp 2

Đạo đức lớp 2

Tự nhiên và Xã hội lớp 2

Hoạt động trải nghiệm lớp 2

Tiếng Anh lớp 2

Âm nhạc lớp 2

Lớp 2 - Cánh diều

Toán lớp 2

Tiếng Việt lớp 2

Hoạt động trải nghiệm lớp 2

Tự nhiên và Xã hội lớp 2

Tiếng Anh lớp 2

Âm nhạc lớp 2

Đạo đức lớp 2

Lớp 2 - Chân trời sáng tạo

Toán lớp 2

Tiếng Việt lớp 2

Đạo đức lớp 2

Tự nhiên và Xã hội lớp 2

Hoạt động trải nghiệm lớp 2

Tiếng Anh lớp 2

Âm nhạc lớp 2

Đề thi các môn lớp 2

Đề thi các môn lớp 2 - Kết nối tri thức

Đề thi các môn lớp 2 - Cánh diều

Đề thi các môn lớp 2 - Chân trời sáng tạo

Tiện ích

Đọc sách online

Bộ đề ôn hè lớp 2 lên lớp 3

Giáo án lớp 2

Lớp 3 - Kết nối tri thức

Toán lớp 3

Tiếng Anh lớp 3

Tiếng Việt lớp 3

Đạo đức lớp 3

Tự nhiên và Xã hội lớp 3

Hoạt động trải nghiệm lớp 3

Âm nhạc lớp 3

Tin học lớp 3

Giáo dục thể chất lớp 3

Công nghệ lớp 3

Lớp 3 - Cánh diều

Toán lớp 3

Tiếng Việt lớp 3

Tiếng Anh lớp 3

Đạo đức lớp 3

Tự nhiên và Xã hội lớp 3

Hoạt động trải nghiệm lớp 3

Âm nhạc lớp 3

Tin học lớp 3

Giáo dục thể chất lớp 3

Công nghệ lớp 3

Lớp 3 - Chân trời sáng tạo

Toán lớp 3

Tiếng Việt lớp 3

Tiếng Anh lớp 3

Đạo đức lớp 3

Tự nhiên và Xã hội lớp 3

Hoạt động trải nghiệm lớp 3

Âm nhạc lớp 3

Tin học lớp 3

Giáo dục thể chất lớp 3