Nội dung bài viết

    Xem thêm

    Giải SBT Toán 10 trang 58 Tập 1 Kết nối tri thức

    Với Giải SBT Toán 10 trang 58 Tập 1 trong Bài 10: Vectơ trong mặt phẳng tọa độ Toán lớp 10 Tập 1 Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng trả lời các câu hỏi & làm bài tập Toán 10 trang 58.

    1 1,371 09/12/2022
    Trang trước
    Chia sẻ
    Trang sau  

    Giải SBT Toán 10 trang 58 Tập 1 Kết nối tri thức

    Bài 4.22 trang 58 SBT Toán 10 Tập 1:

    Trong mặt phẳng toạ độ Oxy cho ba điểm M(4; 0), N(5; 2) và P(2, 3). Tìm toạ độ các đỉnh của tam giác ABC, biết M, N, P theo thứ tự là trung điểm cạnh BC, CA, AB.

    Lời giải:

    Cách 1:

    Gọi A(xA; yA); B(xB; yB) và C(xC; yC) là tọa độ ba đỉnh của tam giác ABC.

    Ta có:

    +) M(4; 0) là trung điểm của BC nên 4=xB+xC20=yB+yC2

    ⇒xB+xC=8yB+yC=0                                 (1)

    +) N(5; 2) là trung điểm của CA nên 5=xA+xC22=yA+yC2

    ⇒xA+xC=10yA+yC=4⇔xC=10−xAyC=4−yA     (2)

    +) P(2; 3) là trung điểm của AB nên 2=xA+xB23=yA+yB2

    ⇒xA+xB=4yA+yB=6⇔xB=4−xAyB=6−yA        (3)

    Thay (2) và (3) vào (1) ta được:

    4−xA+10−xA=86−yA+4−yA=0⇔14−2xA=810−2yA=0

    ⇔xA=3yA=5 ⇒ A(3; 5)

    Khi đó xB=4−3=1yB=6−5=1 ⇒ B(1; 1)

    xC=10−3=7yC=4−5=−1⇒ C(7; –1)

    Vậy A(3; 5), B(1; 1) và C(7; –1).

    Cách 2:

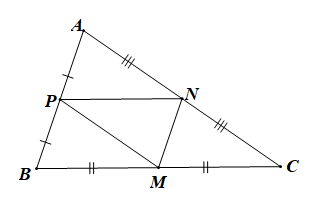
    Sách bài tập Toán 10 Bài 10: Vectơ trong mặt phẳng tọa độ - Kết nối tri thức (ảnh 1)

    Do M, N, P lần lượt là trung điểm của BC, CA, AB

    Nên MN, NP, PM là các đường trung bình của tam giác ABC.

    ⇒ MN // AB, NP // BC, MP // AC.

    +) Do MN // BM và NP // BM nên tứ giác MNPB là hình bình hành

    ⇒MB→=NP→

    Gọi B(xB; yB) và có M(4; 0), N(5; 2) và P(2, 3).

    ⇒MB→=xB−4;yB và NP→=2−5;3−2=−3;1

    Khi đó MB→=NP→⇔xB−4=−3yB=1⇔xB=1yB=1 Þ B(1; 1)

    Tương tự ta cũng có A(3; 5) và C(7; –1).

    Vậy A(3; 5), B(1; 1) và C(7; –1).

    Bài 4.23 trang 58 SBT Toán 10 Tập 1:

    Trong mặt phẳng toạ độ Oxy cho ba điểm A(2;–1), B(1; 4) và C(7; 0).

    a) Tính độ dài các đoạn thẳng AB, BC và CA. Từ đó suy ra tam giác ABC là một tam giác vuông cân.

    b) Tìm toạ độ của điểm D sao cho tứ giác ABDC là một hình vuông.

    Lời giải:

    a) Với A(2;–1), B(1; 4) và C(7; 0) ta có:

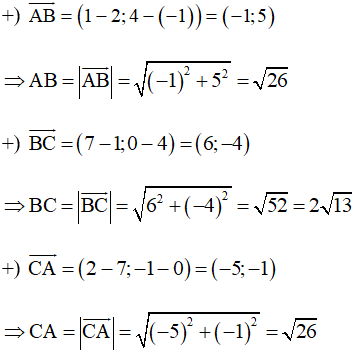
    Sách bài tập Toán 10 Bài 10: Vectơ trong mặt phẳng tọa độ - Kết nối tri thức (ảnh 1)

    Do đó AB = CA =26

    Nên tam giác ABC cân tại A               (1)

    Mặt khác: BC2=2132=52

    Và AB2+AC2=262+262=52

    ⇒ BC2 = AB2 + AC2

    Theo định lí Pythagoras đảo thì tam giác ABC vuông tại A        (2)

    Từ (1) và (2) suy ra tam giác ABC vuông cân tại A với AB=AC=26;BC=213.

    b)

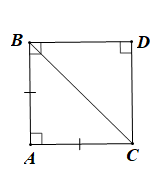
    Sách bài tập Toán 10 Bài 10: Vectơ trong mặt phẳng tọa độ - Kết nối tri thức (ảnh 1)

    Vì ABC là tam giác vuông cân

    Nên để ABDC là hình vuông thì tứ giác ABDC là hình bình hành

    ⇔CA→=DB→

    Gọi D(xD; yD) và có A(2;–1), B(1; 4), C(7; 0).

    ⇒CA→=−5;−1và DB→=1−xD;4−yD

    Do đó CA→=DB→⇔−5=1−xD−1=4−yD

    ⇔xD=6yD=5 ⇒ D(6; 5).

    Vậy tọa độ điểm D cần tìm là D(6; 5).

    Bài 4.24 trang 58 SBT Toán 10 Tập 1:

    Trong mặt phẳng toạ độ Oxy cho hai điểm M(–2; 1) và N(4; 5).

    a) Tìm toạ độ của điểm P thuộc Ox sao cho PM = PN.

    b) Tìm toạ độ của điểm Q sao cho MQ→=2PN→.

    c) Tìm toạ độ của điểm R thoả mãn RM→+2RN→=0→. Từ đó suy ra P, Q, R thẳng hàng.

    Lời giải:

    a) Gọi P(a; 0) là điểm thuộc tia Ox.

    Với M(–2; 1) và N(4; 5) ta có:

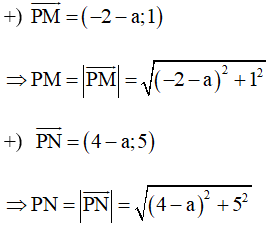
    Sách bài tập Toán 10 Bài 10: Vectơ trong mặt phẳng tọa độ - Kết nối tri thức (ảnh 1)

     Do đó PM = PN ⇔−2−a2+12=4−a2+52

    ⇒ (–2 – a)2 + 12 = (4 – a)2 + 52

    ⇒ 4 + 4a + a2 + 1 = 16 – 8a + a2 + 25

    ⇒ 12a = 36

    ⇒ a = 3.

    Vậy P(3; 0).

    b) Giả sử điểm Q có tọa độ là Q(x; y).

    Với M(–2; 1), N(4; 5) và P(3; 0) ta có:

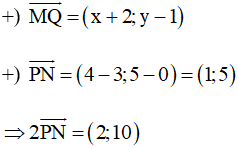
    Sách bài tập Toán 10 Bài 10: Vectơ trong mặt phẳng tọa độ - Kết nối tri thức (ảnh 1)

    Do đó MQ→=2PN→⇔x+2=2y−1=10

    ⇔x=0y=11 ⇒ Q(0; 11).

    Vậy Q(0; 11).

    c) Giả sử R(x0; y0) là điểm cần tìm.

    Với M(–2; 1) và N(4; 5) ta có:

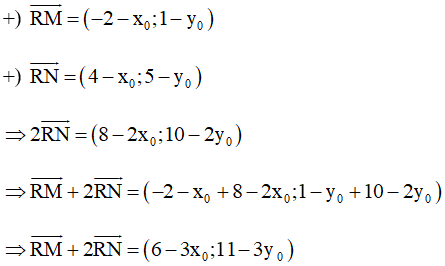
    Sách bài tập Toán 10 Bài 10: Vectơ trong mặt phẳng tọa độ - Kết nối tri thức (ảnh 1)

    Do đó 

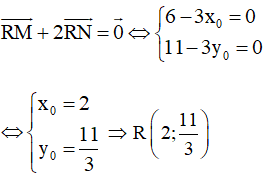
    Sách bài tập Toán 10 Bài 10: Vectơ trong mặt phẳng tọa độ - Kết nối tri thức (ảnh 1)

    +) Ta xét ba điểm: P(3; 0), Q(0; 11) và R2;113

    ⇒PQ→=−3;11và QR→=2;113−11=2;−223

    Có: −32=11−223 nên hai vectơ PQ→ và QR→ cùng phương

    Do đó P, Q, R thẳng hàng

    Vậy ba điểm P, Q, R thẳng hàng.

    Xem thêm lời giải sách bài tập Toán lớp 10 Kết nối tri thức với cuộc sống hay, chi tiết khác:

    Giải SBT Toán 10 trang 59, 60 Tập 1

    Giải SBT Toán 10 trang 61, 62 Tập 1

    Xem thêm lời giải sách bài tập Toán lớp 10 Kết nối tri thức với cuộc sống hay, chi tiết khác:

    Bài 7: Các khái niệm mở đầu

    Bài 8: Tổng và hiệu của hai vectơ

    Bài 9: Tích của một vectơ với một số

    Bài 11: Tích vô hướng của hai vectơ

    Bài tập cuối chương 4

    Tham khảo các loạt bài Toán 10 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 1,371 09/12/2022
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: