Nội dung bài viết

    Xem thêm

    Giải SBT Toán 10 trang 25 Tập 2 Kết nối tri thức

    Với Giải SBT Toán 10 trang 25 Tập 2 trong Bài tập cuối chương 6 Toán lớp 10 Tập 2 Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng trả lời các câu hỏi & làm bài tập Toán 10 trang 25.

    1 389 09/12/2022
    Trang trước
    Chia sẻ
    Trang sau  

    Giải SBT Toán 10 trang 25 Tập 2 Kết nối tri thức

    Bài 6.47 trang 25 SBT Toán 10 Tập 2: Tập nghiệm của bất phương trình x2 – 4x + 3 < 0 là

    A. (1; 3);

    B. (–∞; 1)∪[3; +∞);

    C. [1; 3];

    D. (–∞; 1]∪[4; +∞).

    Lời giải:

    Đáp án đúng là: A

    x2 – 4x + 3 < 0 (*)

    Xét tam thức f(x) = x2 – 4x + 3 < 0 có:

    a = 1 > 0

    Δ = (–4)2 – 4.1.3 = 4 > 0

    f(x) = x2 – 4x + 3 = 0 ⇔ x1 = 1; x2 = 3

    Do đó, x2 – 4x + 3 < 0 ⇔ 1 < x < 3.

    Vậy tập nghiệm của bất phương trình (*) là: (1; 3).

    Bài 6.48 trang 25 SBT Toán 10 Tập 2: Các giá trị của tham số m làm cho biểu thức f(x) = x2 + 4x + m – 5 luôn dương là

    A. m ≥ 9;

    B. m > 9;

    C. Không có m;

    D. m < 9.

    Lời giải:

    Đáp án đúng là: B

    Xét tam thức f(x) = x2 + 4x + m – 5 có:

    a = 1 > 0

    f(x) luôn dương ⇔ Δ < 0

    ⇔ 42 – 4.1.(m – 5) < 0

    ⇔ 16 – 4m + 20 < 0

    ⇔ 4m > 36

    ⇔ m > 9.

    Bài 6.49 trang 25 SBT Toán 10 Tập 2: Phương trình (m + 2) x2 – 3x + 2m – 3 = 0 có hai nghiệm trái dấu khi và chỉ khi

    A. m < –2 hoặc m>32;

    B. m>32;

    C. −2<m<32;

    D. m < 2.

    Lời giải:

    Đáp án đúng là: C

    Phương trình (m + 2) x2 – 3x + 2m – 3 = 0 có hai nghiệm trái dấu khi và chỉ khi

    ac < 0

    ⇔ (m + 2)(2m – 3) < 0

     ⇔ 2m2 – 3m + 4m – 6 < 0

    ⇔ 2m2 + m – 6 < 0

    Xét tam thức f(x) = 2m2 + m – 6 có:

    a = 2 > 0

    Δ = 12 – 4.1.(–6) = 25 > 0

    f(x) = 2m2 + m – 6  = 0 có hai nghiệm là: x1 = –2; x2 = 32.

    Do đó, 2m2 + m – 6 < 0 ⇔ –2 < x < 32 

    Vậy phương trình (m + 2) x2 – 3x + 2m – 3 = 0 có hai nghiệm trái dấu khi và chỉ khi −2<m<32.

    Bài 6.50 trang 25 SBT Toán 10 Tập 2: Bất phương trình mx2 – (2m – 1)x + m + 1 < 0 vô nghiệm khi và chỉ khi

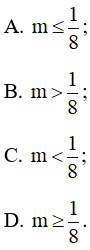
    Sách bài tập Toán 10 Bài tập cuối chương 6 - Kết nối tri thức (ảnh 1)

    Lời giải:

    Đáp án đúng là: D

    +) Khi m = 0, ta có:

    mx2 – (2m – 1)x + m + 1 < 0

    ⇔ x + 1 < 0

    ⇔ x < –1

    Do đó, m = 0 không thỏa mãn yêu cầu đề bài

    +) Khi m ≠ 0, ta có:

    Xét tam thức: f(x) = mx2 – (2m – 1)x + m + 1 có:

    a = m,

    ∆ = [–(2m – 1)2] – 4.m.(m + 1) = 4m2 – 4m + 1 – 4m2 – 4m = –8m + 1

    Để mx2 – (2m – 1)x + m + 1 < 0 vô nghiệm khi và chỉ khi mx2 – (2m – 1)x + m + 1 ≥ 0 với mọi số thực x

    ⇔a>0Δ≤0⇔m>0−8m+1≤0⇔m>0m≥18⇔m≥18

    Vậy khi m≥18 thì bất phương trình mx2 – (2m – 1)x + m + 1 < 0 vô nghiệm.

    Bài 6.51 trang 25 SBT Toán 10 Tập 2: Số nghiệm của phương trình x2+4x−2=x−3 là

    A. 0;

    B. 1;

    C. 2;

    D. 3.

    Lời giải:

    Đáp án đúng là: A

    x2+4x−2=x−3 (*)

    Bình phương hai vế (*) ta có:

    x2 + 4x – 2 = (x – 3)2

    ⇔ x2 + 4x – 2 = x2 – 6x + 9

    ⇔ 10x = 11

    ⇔ x=1110

    Thay x=1110 vào (*) ta có:

    11102+4.1110−2=1110−3⇔1910=−1910 (không thỏa mãn)

    Vậy phương trình (*) vô nghiệm.

    Bài 6.52 trang 25 SBT Toán 10 Tập 2: Tập nghiệm của phương trình 2x2−9x−9=3−xlà

    A. S = {6};

    B. S = ∅;

    C. S = {–3};

    D. S = {–3; 6}.

    Lời giải:

    Đáp án đúng là: C

    2x2−9x−9=3−x (*)

    Bình phương hai vế (*) ta có:

    2x2 – 9x – 9 =  (3 – x)2

    ⇔ 2x2 – 9x – 9 = 9 – 6x + x2

    ⇔ x2 – 3x – 18 = 0

    ⇔ x = 6 hoặc x = –3

    Thay x = 6 vào (*) ta có:

    2.62−9.6−9=3−6⇔3=−3 (không thỏa mãn)

    Thay x = –3 vào (*) ta có:

    2.(−3)2−9.(−3)−9=3−(−3)⇔6=6 tm

    Vậy tập nghiệm của phương trình (*) là: S = {–3}.

    Bài 6.53 trang 25 SBT Toán 10 Tập 2: Tập nghiệm của phương trình 2x2−5x+1=x2+2x−9 là

    A. S = {2};

    B. S = {5};

    C. S = ∅;

    D. S = {2; 5}.

    Lời giải:

    Đáp án đúng là: B

    2x2−5x+1=x2+2x−9 (*)

    Bình phương hai vế của (*) ta có:

    2x2 – 5x + 1 = x2 + 2x – 9

    ⇔ x2 – 7x + 10 = 0

    ⇔ x = 5 hoặc x = 2

    Thay x = 5 vào (*) ta có:

    2.52−5.5+1=52+2.5−9⇔26=26 tm

    Thay x = 2 vào (*) ta có:

    2.22−5.2+1=22+2.2−9⇔−1=−1 (không thể tồn tại)

    Vậy tập nghiệm của phương trình (*) là: S = {5}.

    B – Tự luận

    Bài 6.54 trang 25 SBT Toán 10 Tập 2: Tìm tập xác định của các hàm số sau:

    a) y=−x2+3x−2;

    b) y=x−1x2−1.

    Lời giải:

    a)

    Điều kiện xác định của hàm số là: –x2 + 3x – 2 ≥ 0

    Xét tam thức f(x) = –x2 + 3x – 2  có:

    a = –1 < 0

    ∆ = 32 – 4.(–1).(–2) = 1 > 0

    f(x) = 0 có hai nghiệm phân biệt là: x1 = 2 ; x2 = 1

    Do đó, ta có:

    –x2 + 3x – 2 ≥ 0

    ⇔ 1 ≤ x ≤ 2

    Vậy tập xác định của hàm số là: D = [1; 2].

    b)

    Điều kiện xác định của hàm số là:

    x2 – 1 > 0

    ⇔ x2 > 1

    ⇔ x < –1 hoặc x > 1

    Vậy tập xác định của hàm số là: D = (–∞; –1)∪(1; +∞).

    Xem thêm lời giải sách bài tập Toán lớp 10 Kết nối tri thức với cuộc sống hay, chi tiết khác: 

    Giải SBT Toán 10 trang 22 Tập 2

    Giải SBT Toán 10 trang 23 Tập 2

    Giải SBT Toán 10 trang 24 Tập 2

    Giải SBT Toán 10 trang 26 Tập 2

    Giải SBT Toán 10 trang 27 Tập 2

    Xem thêm lời giải sách bài tập Toán lớp 10 Kết nối tri thức với cuộc sống hay, chi tiết khác: 

    Bài tập cuối chương 5

    Bài 15: Hàm số

    Bài 16: Hàm số bậc hai

    Bài 17: Dấu của tam thức bậc hai

    Bài 18: Phương trình quy về phương trình bậc hai

    Tham khảo các loạt bài Toán 10 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 389 09/12/2022
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: