Cho hình hộp ABCD.A’B’C’D’. Chứng minh rằng: a) vecto AB + DD' + C'D' = CC'

Giải Toán 12 Kết nối tri thức Bài 6: Vectơ trong không gian

Bài 2.4 trang 58 Toán 12 Tập 1: Cho hình hộp ABCD.A’B’C’D’. Chứng minh rằng:
a) $\overrightarrow{AB}+\overrightarrow{D{D}^{\prime }}+\overrightarrow{C^{\prime }{D}^{\prime }}=\overrightarrow{C{C}^{\prime }}$;
b) $\overrightarrow{AB}+\overrightarrow{C{D}^{\prime }}-\overrightarrow{C{C}^{\prime }}=\overrightarrow{0}$;
c) $\overrightarrow{BC}-\overrightarrow{C{C}^{\prime }}+\overrightarrow{DC}=\overrightarrow{A^{\prime }C}$

* Lời giải:

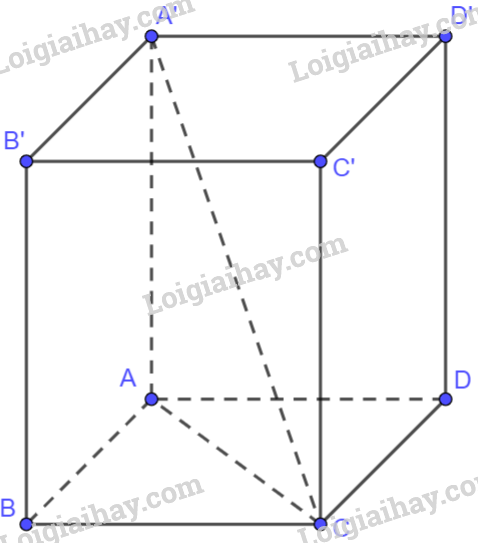
a) Vì ABCD là hình bình hành nên $\overrightarrow{AB}=\overrightarrow{DC}$

Vì CDD’C’ là hình bình hành nên $\overrightarrow{C^{\prime }{D}^{\prime }}=\overrightarrow{CD},\overrightarrow{D{D}^{\prime }}=\overrightarrow{C{C}^{\prime }}$

Ta có:$\overrightarrow{AB}+\overrightarrow{D{D}^{\prime }}+\overrightarrow{C^{\prime }{D}^{\prime }}=\overrightarrow{DC}+\overrightarrow{C{C}^{\prime }}+\overrightarrow{CD}=\left(\overrightarrow{CD}+\overrightarrow{DC}\right)+\overrightarrow{C{C}^{\prime }}=\overrightarrow{C{C}^{\prime }}$

b) Ta có: $\overrightarrow{AB}+\overrightarrow{C{D}^{\prime }}-\overrightarrow{C{C}^{\prime }}=\overrightarrow{AB}+\overrightarrow{C^{\prime }{D}^{\prime }}=\overrightarrow{AB}+\overrightarrow{CD}=\overrightarrow{0}$

c) Vì ABCD là hình bình hành nên $\overrightarrow{CB}+\overrightarrow{CD}=\overrightarrow{CA}$

Vì A’ACC’ là hình bình hành nên $\overrightarrow{CA}+\overrightarrow{C{C}^{\prime }}=\overrightarrow{C{A}^{\prime }}$

$\overrightarrow{BC}-\overrightarrow{C{C}^{\prime }}+\overrightarrow{DC}=-\left(\overrightarrow{CB}+\overrightarrow{CD}\right)-\overrightarrow{C{C}^{\prime }}=-\overrightarrow{CA}-\overrightarrow{C{C}^{\prime }}=-\left(\overrightarrow{CA}+\overrightarrow{C{C}^{\prime }}\right)=-\overrightarrow{C{A}^{\prime }}=\overrightarrow{A^{\prime }C}$

* Phương pháp giải:

Sử dụng các phép tính toán vectơ trong không gian:

+ Tổng của hai vectơ

Trong không gian, cho hai vectơ $\overrightarrow{a},\overrightarrow{\mathbf{b}}$. Lấy một điểm A tùy ý, vẽ $\overrightarrow{AB}=\overrightarrow{a}$, $\overrightarrow{BC}=\overrightarrow{b}$.

Vectơ $\overrightarrow{AC}$ được gọi là tổng của hai vectơ $\overrightarrow{a}$ và $\overrightarrow{b}$, kí hiệu là $\overrightarrow{AC}=\overrightarrow{a}+\overrightarrow{b}$.

+ Nếu ABCD là hình bình hành thì $\overrightarrow{AB}+\overrightarrow{AD}=\overrightarrow{AC}$ (quy tắc hình bình hành).

+ Với ba điểm O, A, B trong không gian, ta có: $\overrightarrow{OA}-\overrightarrow{OB}=\overrightarrow{BA}$ (quy tắc hiệu).

*Một số lý thuyết và dạng bài tập về vectơ trong không gian:

• Vectơ trong không gian

Vectơ trong không gian là một đoạn thẳng có hướng.

Chú ý:

Cho đoạn thẳng AB trong không gian. Nếu ta chọn điểm đầu là A, điểm cuối là B thì ta có một vectơ, kí hiệu là $\overrightarrow{AB}$ , đọc là “vectơ AB”.

Khi không cần chỉ rõ điểm đầu và điểm cuối của vectơ, vectơ còn được kí hiệu là $\overrightarrow{a}$, $\overrightarrow{b},\overrightarrow{u},\overrightarrow{v},$...

• Các khái niệm có liên quan đến vectơ trong không gian như: giá của vectơ, độ dài của vectơ, vectơ cùng phương, vectơ cùng hướng, vectơ – không, hai vectơ bằng nhau, hai vectơ đối nhau, … được phát biểu tương tự như trong mặt phẳng.

Chú ý:

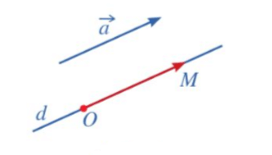
Cho điểm O và vectơ $\overrightarrow{a}$ . Khi đó, tồn tại duy nhất điểm M trong không gian sao cho $\overrightarrow{OM}=\overrightarrow{a}$ .

Để xác định điểm M, ta làm như sau (xem hình dưới):

• Qua O kẻ đường thẳng d song song hoặc trùng với giá của vectơ $\overrightarrow{a}$.

• Lấy điểm M trên đường thẳng d sao cho hai vectơ $\overrightarrow{OM}$,$\overrightarrow{a}$ là cùng hướng và độ dài đoạn thẳng OM bằng độ dài đoạn thẳng vectơ $\overrightarrow{a}$.

- Tổng của hai vectơ

Trong không gian, cho hai vectơ $\overrightarrow{a},\overrightarrow{\mathbf{b}}$. Lấy một điểm A tùy ý, vẽ $\overrightarrow{AB}=\overrightarrow{a}$, $\overrightarrow{BC}=\overrightarrow{b}$.

Vectơ $\overrightarrow{AC}$ được gọi là tổng của hai vectơ $\overrightarrow{a}$ và $\overrightarrow{b}$, kí hiệu là $\overrightarrow{AC}=\overrightarrow{a}+\overrightarrow{b}$.

Chú ý:

• Phép lấy tổng hai vectơ còn được gọi là phép cộng vectơ.

• Phép cộng vectơ trong không gian cũng có các tính chất như phép cộng vectơ trong mặt phẳng, chẳng hạn: Phép cộng vectơ trong không gian cũng có các tính chất giao hoán, kết hợp, cộng với vectơ – không. Do đó, ta cũng định nghĩa được tổng của ba vectơ trong không gian.

• Khi thực hiện phép cộng vectơ trong không gian, ta vẫn có thể áp dụng quy tắc ba điểm, quy tắc hình bình hành như đối với vectơ trong mặt phẳng.

Đối với vectơ trong không gian, ta cũng có các quy tắc sau:

• Với ba điểm A, B, C trong không gian, ta có: $\overrightarrow{AB}+\overrightarrow{BC}=\overrightarrow{AC}$ (quy tắc ba điểm);

• Nếu ABCD là hình bình hành thì $\overrightarrow{AB}+\overrightarrow{AD}=\overrightarrow{AC}$ (quy tắc hình bình hành).

• Nếu ABCD.A'B'C'D' là hình hộp thì $\overrightarrow{AB}+\overrightarrow{AD}+\overrightarrow{AA\text{'}}=\overrightarrow{AC\text{'}}$ (quy tắc hình hộp).

- Hiệu của hai vectơ

• Trong không gian, cho hai vectơ $\overrightarrow{a},\overrightarrow{b}$. Hiệu của vectơ $\overrightarrow{a}$ và vectơ $\overrightarrow{b}$ là tổng của vectơ $\overrightarrow{a}$với vectơ đối của vectơ $\overrightarrow{b}$, kí hiệu là $\overrightarrow{a}-\overrightarrow{b}$.

Phép lấy hiệu của hai vectơ còn được gọi là phép trừ vectơ.

Đối với vectơ trong không gian, ta có quy tắc sau:

• Với ba điểm O, A, B trong không gian, ta có: $\overrightarrow{OA}-\overrightarrow{OB}=\overrightarrow{BA}$ (quy tắc hiệu).

Tích của một số với một vectơ trong không gian

Tương tự như trong mặt phẳng, trong không gian ta cũng có định nghĩa sau:

Cho số thực k ≠ 0 và vectơ $\overrightarrow{a}\ne \overrightarrow{0}$. Tích của số k với vectơ $\overrightarrow{a}$ là một vectơ, kí hiệu là $k\overrightarrow{a}$, được xác định như sau:

• Cùng hướng với vectơ $\overrightarrow{a}$ nếu k > 0, ngược hướng với vectơ $\overrightarrow{a}$ nếu k < 0;

• Có độ dài bằng |k| . | $\overrightarrow{a}$|.

Quy ước: 0.$\overrightarrow{a}$ = $\overrightarrow{0}$, k. $\overrightarrow{0}$ = $\overrightarrow{0}$ . Do đó, k.$\overrightarrow{a}$ = $\overrightarrow{0}$ khi và chỉ khi k = 0 hoặc $\overrightarrow{a}$= $\overrightarrow{0}$ .

Chú ý:

• Phép lấy tích của một số với một vectơ gọi là phép nhân một số với một vectơ.

• Phép nhân một số với một vectơ trong không gian có các tính chất sau:

Với hai vectơ bất kì $\overrightarrow{a}$ ,$\overrightarrow{b}$ và hai số thực h, k ta có:

+ k($\overrightarrow{a}$ + $\overrightarrow{b}$) = k $\overrightarrow{a}$ + k$\overrightarrow{b}$ ; k($\overrightarrow{a}$- $\overrightarrow{b}$ ) = k$\overrightarrow{a}$ − k$\overrightarrow{b}$ ;

+ (h + k)$\overrightarrow{a}$ = h $\overrightarrow{a}$ + k $\overrightarrow{a}$;

+ h(k $\overrightarrow{a}$) = (hk) $\overrightarrow{a}$;

+ 1$\overrightarrow{a}$ =$\overrightarrow{a}$ ; (−1) $\overrightarrow{a}$ = − $\overrightarrow{a}$.

• Hai vectơ $\overrightarrow{a}$, $\overrightarrow{b}$ khác $\overrightarrow{0}$ là cùng phương khi và chỉ khi có một số thực k ≠ 0 sao cho $\overrightarrow{a}=k\overrightarrow{b}$ .

Tích vô hướng của hai vectơ trong không gian

Trong không gian, cho hai vectơ $\overrightarrow{a}$,$\overrightarrow{b}$ khác $\overrightarrow{0}$. Lấy một điểm O tùy ý và vẽ hai vectơ $\overrightarrow{OA}=\overrightarrow{a}$, $\overrightarrow{OB}=\overrightarrow{b}$. Góc giữa hai vectơ $\overrightarrow{a}$,$\overrightarrow{b}$ trong không gian là góc giữa hai vectơ $\overrightarrow{OA},$$\overrightarrow{OB}$, kí hiệu là $\left(\overrightarrow{a},\overrightarrow{b}\right)$ .

Chú ý: 0^o ≤ $\left(\overrightarrow{a},\overrightarrow{b}\right)$ ≤ 180^o.

Xem thêm các bài viết liên quan hay, chi tiết

Lý thuyết Vectơ và các phép toán vectơ trong không gian– Toán lớp 12 Kết nối tri thức

Toán 12 Bài 6 giải vở bài tập (Kết nối tri thức): Vectơ trong không gian