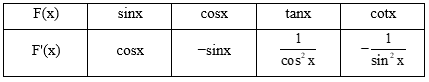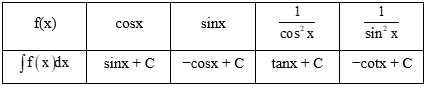Toán 12 Bài 11 (Kết nối tri thức): Nguyên hàm

Giải Toán 12 Bài 11: Nguyên hàm

Mở đầu trang 4 Toán 12 Tập 2: Một máy bay di chuyển ra đến đường băng và bắt đầu chạy đà để cất cánh. Giả sử vận tốc của máy bay khi chạy đà được cho bởi v(t) = 5 + 3t (m/s), với t là thời gian (tính bằng giây) kể từ khi máy bay bắt đầu chạy đà. Sau 30 giây thì máy bay cất cánh rời đường băng. Quãng đường máy bay đã di chuyển kể từ khi bắt đầu chạy đà đến khi rời đường băng là bao nhiêu mét?

Lời giải:

Sau khi học xong bài này, ta giải quyết bài toán này như sau:

Gọi S(t) (0 ≤ t ≤ 30) là quãng đường máy bay di chuyển được sau t giây kể từ lúc bắt đầu chạy đà.

Ta có v(t) = S'(t). Do đó, S(t) là một nguyên hàm của hàm số vận tốc v(t). Sử dụng tính chất của nguyên hàm ta được

$S\left(t\right)=\int v\left(t\right)dt=\int \left(5+3t\right)dt=5\int dt+3\int tdt=5t+\frac{3}{2}{t}^2+C.$

Theo giả thiết, S(0) = 0 nên C = 0 và ta được $S\left(t\right)=\frac{3}{2}{t}^2+5t\left(m\right)$.

Máy bay rời đường băng khi t = 30 giây nên $S=S\left(30\right)=\frac{3}{2}{.30}^2+5.30=1500\left(m\right)$

Vậy quãng đường máy bay đã di chuyển kể từ khi bắt đầu chạy đà đến khi rời đường băng là 1500 m.

HĐ1 trang 4 Toán 12 Tập 2: Cho hai hàm số f(x) = x² + 1 và $F\left(x\right)=\frac{1}{3}{x}^3+x$, với x ∈ ℝ.

a) Tính đạo hàm của hàm số F(x).

b) F'(x) và f(x) có bằng nhau không?

Lời giải:

a) Ta có $F^{\text{'}}\left(x\right)={\left(\frac{1}{3}{x}^3+x\right)}^{\text{'}}=x^2+1$.

b) Ta có F'(x) = f(x) = x² + 1.

Luyện tập 1 trang 5 Toán 12 Tập 2: Hàm số nào dưới đây là một nguyên hàm của hàm số $f\left(x\right)=x+\frac{1}{x}$ trên khoảng (0; +∞).

a) $F\left(x\right)=\frac{1}{2}{x}^2+\ln x$; b) $G\left(x\right)=\frac{x^2}{2}-\ln x$.

Lời giải:

Ta có $F^{\text{'}}\left(x\right)={\left(\frac{1}{2}{x}^2+\ln x\right)}^{\text{'}}=x+\frac{1}{x}$, $G^{\text{'}}\left(x\right)={\left(\frac{x^2}{2}-\ln x\right)}^{\text{'}}=x-\frac{1}{x}$.

Vì $F^{\text{'}}\left(x\right)=f\left(x\right)=x+\frac{1}{x}$ trên khoảng (0; +∞) nên hàm số F(x) là một nguyên hàm của f(x) trên khoảng (0; +∞).

Hàm số G(x) không là nguyên hàm của f(x) trên khoảng (0; +∞) vì với x = 1 ∈ (0; +∞), ta có G'(1) = 0 ≠ 2 = f(1).

HĐ2 trang 5 Toán 12 Tập 2:

a) Chứng minh rằng hàm số $F\left(x\right)=\frac{x^4}{4}$ là một nguyên hàm của hàm số f(x) = x³ trên ℝ.

b) Hàm số $G\left(x\right)=\frac{x^4}{4}+C$ (với C là hằng số) có là một nguyên hàm của hàm số f(x) trên ℝ không? Vì sao?

Lời giải:

a) Vì $F^{\text{'}}\left(x\right)={\left(\frac{x^4}{4}\right)}^{\text{'}}=x^3=f\left(x\right)$ nên hàm số $F\left(x\right)=\frac{x^4}{4}$ là một nguyên hàm của hàm số f(x) = x³ trên ℝ.

b) Vì $G^{\text{'}}\left(x\right)={\left(\frac{x^4}{4}+C\right)}^{\text{'}}=x^3=f\left(x\right)$ nên hàm số $G\left(x\right)=\frac{x^4}{4}+C$ (với C là hằng số) có là một nguyên hàm của hàm số f(x) trên ℝ.

Luyện tập 2 trang 6 Toán 12 Tập 2: Tìm $\int x^{3}dx$.

Lời giải:

Vì ${\left(\frac{x^4}{4}\right)}^{\text{'}}=x^3$ nên $F\left(x\right)=\frac{x^4}{4}$ là một nguyên hàm của hàm số f(x) = x³ trên ℝ.

Do đó, $\int x^{3}dx=\frac{x^4}{4}+C$.

HĐ3 trang 6 Toán 12 Tập 2: Cho f(x) là hàm số liên tục trên K, k là một hằng số khác 0. Giả sử F(x) là một nguyên hàm của f(x) trên K.

a) Chứng minh kF(x) là một nguyên hàm của hàm số kf(x) trên K.

b) Nêu nhận xét về $\int kf\left(x\right)dx$ và $k\int f\left(x\right)dx$.

Lời giải:

a) Vì F(x) là một nguyên hàm của f(x) trên K nên F'(x) = f(x).

Ta cần chứng minh (kF(x))' = kf(x).

Ta có (kF(x))' = k(F(x))' = kf(x).

Vậy kF(x) là một nguyên hàm của hàm số kf(x) trên K.

b) Vì F(x) là một nguyên hàm của f(x) trên K nên $\int f\left(x\right)dx=F\left(x\right)+C$.

Có $\int kf\left(x\right)dx=kF\left(x\right)+C^{\text{'}}$.

Vì C' ta có thể viết lại bằng kC. Tức là C' = kC.

Do đó $\int kf\left(x\right)dx=kF\left(x\right)+kC=k\left(F\left(x\right)+C\right)=k\int f\left(x\right)dx$.

Vậy $\int kf\left(x\right)dx=k\int f\left(x\right)dx$.$\int x^{n}dx$.

Luyện tập 3 trang 7 Toán 12 Tập 2: Cho hàm số f(x) = xⁿ (n ∈ ℕ*).

a) Chứng minh rằng hàm số $F\left(x\right)=\frac{x^{n+1}}{n+1}$ là một nguyên hàm của hàm số f(x). Từ đó tìm $\int x^{n}dx$.

b) Từ kết quả câu a, tìm $\int k{x}^{n}dx$ (k là hằng số thực khác 0).

Lời giải:

a) Vì $F^{\text{'}}\left(x\right)={\left(\frac{x^{n+1}}{n+1}\right)}^{\text{'}}=x^n$ nên hàm số $F\left(x\right)=\frac{x^{n+1}}{n+1}$ là một nguyên hàm của hàm số f(x).

Ta có $\int x^{n}dx=\frac{x^{n+1}}{n+1}+C$.

b) Ta có $\int k{x}^{n}dx=k\int x^{n}dx=k\frac{x^{n+1}}{n+1}+C$.

HĐ4 trang 7 Toán 12 Tập 2: Cho f(x) và g(x) là hai hàm số liên tục trên K. Giả sử F(x) là một nguyên hàm của f(x), G(x) là một nguyên hàm của g(x) trên K.

a) Chứng minh F(x) + G(x) là một nguyên hàm của hàm số f(x) + g(x) trên K.

b) Nêu nhận xét về $\int \left[f\left(x\right)+g\left(x\right)\right]dx$ và $\int f\left(x\right)dx+\int g\left(x\right)dx$.

Lời giải:

a) Vì F(x) là một nguyên hàm của f(x) nên F'(x) = f(x) và G(x) là một nguyên hàm của g(x) nên G'(x) = g(x).

Ta có (F(x) + G(x))' = F'(x) + G'(x) = f(x) + g(x).

Do đó F(x) + G(x) là một nguyên hàm của hàm số f(x) + g(x) trên K.

b) Ta có $\int \left[f\left(x\right)+g\left(x\right)\right]dx=F\left(x\right)+G\left(x\right)+C$ với C là hằng số bất kì.

Có $\int f\left(x\right)dx=F\left(x\right)+C_1;\int g\left(x\right)dx=G\left(x\right)+C_2$ với C₁; C₂ là các hằng số bất kì.

Do đó $\int f\left(x\right)dx+\int g\left(x\right)dx=F\left(x\right)+C_1+G\left(x\right)+C_2=F\left(x\right)+G\left(x\right)+\left(C_1+C_2\right)$.

Ta có thể biểu diễn C = C₁ + C₂.

Do đó $\int f\left(x\right)dx+\int g\left(x\right)dx=F\left(x\right)+G\left(x\right)+C$.

Vậy $\int \left[f\left(x\right)+g\left(x\right)\right]dx=\int f\left(x\right)dx+\int g\left(x\right)dx$.

Luyện tập 4 trang 7 Toán 12 Tập 2: Tìm

a) $\int \left(3x^2+1\right)dx$; b) $\int {\left(2x-1\right)}^{2}dx$

Lời giải:

a) $\int \left(3x^2+1\right)dx=3\int x^{2}dx+\int dx=x^3+x+C$.

b) $\int {\left(2x-1\right)}^{2}dx=\int \left(4x^2-4x+1\right)dx$

$=4\int x^{2}dx-4\int xdx+\int dx=\frac{4x^3}{3}-2x^2+x+C$

Vận dụng trang 8 Toán 12 Tập 2: Doanh thu bán hàng của một công ty khi bán một loại sản phẩn là số tiền R(x) (triệu đồng) thu được khi x đơn vị sản phẩm được bán ra. Tốc độ biến động (thay đổi) của doanh thu khi x đơn vị sản phẩm đã được bán là hàm số M_R(x) = R'(x). Một công ty công nghệ cho biết, tốc độ biến đổi của doanh thu khi bán một loại con chíp của hãng được cho bởi M_R(x) = 300 – 0,1x, ở đó x là số lượng chíp đã bán. Tìm doanh thu của công ty khi đã bán 1000 con chíp.

Lời giải:

Doanh thu của công ty là $R\left(x\right)=\int \left(300-\mathrm{0,1}x\right)dx=300x-\frac{1}{20}{x}^2+C$.

Vì R(0) = 0 nên C = 0.

Do đó $R\left(x\right)=300x-\frac{1}{20}{x}^2$.

Doanh thu của công ty khi đã bán 1000 con chíp là:

$R\left(1000\right)=300.1000-\frac{1}{20}{.1000}^2=250000$ triệu đồng.

Câu hỏi trang 8 Toán 12 Tập 2: Bằng cách viết lại các hàm số sau dưới dạng hàm số lũy thừa y = x^α (x > 0), hãy tính đạo hàm của các hàm số sau với x > 0: $y=\frac{1}{x^4};y=x^{\sqrt{2}};y=\frac{1}{\sqrt[3]{x}}$

Lời giải:

Có $y=\frac{1}{x^4}=x^{-4}$$\Rightarrow y^{\text{'}}={\left(x^{-4}\right)}^{\text{'}}=-4x^{-5}=-\frac{4}{x^5}$

$y^{\text{'}}={\left(x^{\sqrt{2}}\right)}^{\text{'}}=\sqrt{2}{x}^{\sqrt{2}-1}$

$y=\frac{1}{\sqrt[3]{x}}=x^{\frac{-1}{3}}$$\Rightarrow y^{\text{'}}={\left(x^{\frac{-1}{3}}\right)}^{\text{'}}=-\frac{1}{3}{x}^{\frac{-4}{3}}=\frac{-1}{3x^{\frac{4}{3}}}$

HĐ5 trang 8 Toán 12 Tập 2:

a) Với α ≠ −1, tính đạo hàm của hàm số $y=\frac{x^{\alpha +1}}{\alpha +1}\left(x>0\right)$.

b) Cho hàm số y = ln|x| (x ≠ 0). Tính đạo hàm của hàm số này trong hai trường hợp: x > 0 và x < 0.

Lời giải:

a) $y^{\text{'}}={\left(\frac{x^{\alpha +1}}{\alpha +1}\right)}^{\text{'}}=\frac{\left(\alpha +1\right).x^{\alpha }}{\alpha +1}=x^{\alpha }$

b) Với x > 0 thì y = ln|x| = lnx. Do đó $y^{\text{'}}={\left(\ln x\right)}^{\text{'}}=\frac{1}{x}$.

Với x < 0 thì y = ln|x| = ln(−x). Do đó $y^{\text{'}}={\left(\ln \left(-x\right)\right)}^{\text{'}}=\frac{{\left(-x\right)}^{\text{'}}}{-x}=\frac{1}{x}$.

Luyện tập 5 trang 9 Toán 12 Tập 2: Tìm:

a) $\int \frac{1}{x^4}dx$;

b) $\int x\sqrt{x}dx\left(x>0\right)$;

c) $\int \left(\frac{3}{x}-5\sqrt[3]{x}\right)dx\left(x>0\right)$.

Lời giải:

a) $\int \frac{1}{x^4}dx=\int x^{-4}dx=\frac{x^{-3}}{-3}+C=\frac{-1}{3x^3}+C$

b) $\int x\sqrt{x}dx=\int x^{\frac{3}{2}}dx=\frac{x^{\frac{3}{2}+1}}{\frac{3}{2}+1}+C=\frac{2}{5}{x}^{\frac{5}{2}}+C=\frac{2}{5}{x}^2\sqrt{x}+C$

c) $\int \left(\frac{3}{x}-5\sqrt[3]{x}\right)dx=3\int \frac{1}{x}dx-5\int x^{\frac{1}{3}}dx$

$=3\ln \left|x\right|-5.\frac{x^{\frac{1}{3}+1}}{\frac{1}{3}+1}+C=3\ln \left|x\right|-\frac{15}{4}{x}^{\frac{4}{3}}+C=3\ln \left|x\right|-\frac{15}{4}x\sqrt[3]{x}+C$

HĐ6 trang 9 Toán 12 Tập 2:

a) Tính đạo hàm của các hàm số sau và nêu kết quả tương ứng vào bảng dưới đây.

b) Sử dụng kết quả ở câu a, tìm nguyên hàm của các hàm số cho trong bảng dưới đây.

Lời giải:

a)

b)

Luyện tập 6 trang 9 Toán 12 Tập 2: Tìm:

a) $\int \left(3\cos x-4\sin x\right)dx$; b) $\int \left(\frac{1}{{\cos }^{2}x}-\frac{1}{{\sin }^{2}x}\right)dx$.

Lời giải:

a) $\int \left(3\cos x-4\sin x\right)dx$$=3\int \cos xdx-4\int \sin xdx$$=3\sin x+4\cos x+C$

b) $\int \left(\frac{1}{{\cos }^{2}x}-\frac{1}{{\sin }^{2}x}\right)dx$$=\int \frac{1}{{\cos }^{2}x}dx-\int \frac{1}{{\sin }^{2}x}dx$$=\tan x+\cot x+C$

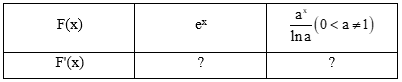
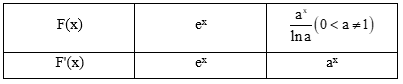
HĐ7 trang 10 Toán 12 Tập 2:

a) Tính đạo hàm của các hàm số sau và nêu kết quả tương ứng vào bảng dưới đây.

b) Sử dụng kết quả ở câu a, tìm nguyên hàm của các hàm số cho trong bảng dưới đây.

Lời giải:

a)

b)

Luyện tập 7 trang 10 Toán 12 Tập 2: Tìm:

a) $\int 4^{x}dx$;

b) $\int \frac{1}{e^x}dx$;

c) $\int \left({2.3}^x-\frac{1}{3}{.7}^x\right)dx$

Lời giải:

a)$\int 4^{x}dx=\frac{4^x}{\ln 4}+C$;

b) $\int \frac{1}{e^x}dx=\int e^{-x}dx=-e^{-x}+C$

c) $\int \left({2.3}^x-\frac{1}{3}{.7}^x\right)dx=2\int 3^{x}dx-\frac{1}{3}\int 7^{x}dx$$=2.\frac{3^x}{\ln 3}-\frac{1}{3}.\frac{7^x}{\ln 7}+C$

Bài tập

Bài 4.1 trang 11 Toán 12 Tập 2: Trong mỗi trường hợp sau, hàm số F(x) có là một nguyên hàm của hàm số f(x) trên khoảng tương ứng không? Vì sao?

a) F(x) = xlnx và f(x) = 1 + lnx trên khoảng (0; +∞);

b) F(x) = e^sinx và f(x) = e^cosx trên ℝ.

Lời giải:

a) Có F'(x) = (xlnx)' = $\ln x+x.\frac{1}{x}=1+\ln x$ = f(x).

Do đó, hàm số F(x) = xlnx là một nguyên hàm của hàm số f(x) = 1 + lnx trên khoảng (0; +∞).

b) Có F'(x) = (e^sinx)' = e^sinx.(sinx)' = cosx.e^sinx ≠ f(x) = e^cosx.

Do đó, hàm số F(x) = e^sinx không là nguyên hàm của hàm số f(x) = e^cosx trên ℝ.

Bài 4.2 trang 11 Toán 12 Tập 2: Tìm nguyên hàm của các hàm số sau:

a) f(x) = 3x² + 2x – 1; b) f(x) = x³ – x;

c) f(x) = (2x + 1)²; d) $f\left(x\right)={\left(2x-\frac{1}{x}\right)}^2$

Lời giải:

a) $\int \left(3x^2+2x-1\right)dx=3\int x^{2}dx+2\int xdx-\int dx=x^3+x^2-x+C$

b) $\int \left(x^3-x\right)dx=\int x^{3}dx-\int xdx=\frac{x^4}{4}-\frac{x^2}{2}+C$

c) $\int {\left(2x+1\right)}^{2}dx=\int \left(4x^2+4x+1\right)dx$

$=4\int x^{2}dx+4\int xdx+\int dx=\frac{4}{3}{x}^3+2x^2+x+C$

d) $\int {\left(2x-\frac{1}{x}\right)}^{2}dx=\int \left(4x^2-4+\frac{1}{x^2}\right)dx$$=4\int x^{2}dx-4\int dx+\int x^{-2}dx$$=\frac{4}{3}{x}^3-4x-\frac{1}{x}+C$

Bài 4.3 trang 11 Toán 12 Tập 2: Tìm:

a) $\int \left(3\sqrt{x}+\frac{1}{\sqrt[3]{x}}\right)dx$; b) $\int \sqrt{x}\left(7x^2-3\right)dx\left(x>0\right)$;

c) $\int \frac{{\left(2x+1\right)}^2}{x^2}dx$; d) $\int \left(2^x+\frac{3}{x^2}\right)dx$

Lời giải:

a) $\int \left(3\sqrt{x}+\frac{1}{\sqrt[3]{x}}\right)dx$$=3\int x^{\frac{1}{2}}dx+\int x^{-\frac{1}{3}}dx=2x^{\frac{3}{2}}+\frac{3}{2}{x}^{\frac{2}{3}}+C$$=2x\sqrt{x}+\frac{3}{2}\sqrt[3]{x^2}+C$

b) $\int \sqrt{x}\left(7x^2-3\right)dx$$=7\int x^{\frac{5}{2}}dx-3\int x^{\frac{1}{2}}dx=$$2x^{\frac{7}{2}}-2x^{\frac{3}{2}}+C=2\sqrt{x^7}-2\sqrt{x^3}+C$

c) $\int \frac{{\left(2x+1\right)}^2}{x^2}dx$$=\int \frac{4x^2+4x+1}{x^2}dx$$=\int \left(4+\frac{4}{x}+\frac{1}{x^2}\right)dx$

$=4\int dx+4\int \frac{1}{x}dx+\int \frac{1}{x^2}dx$$=4x+4\ln \left|x\right|-\frac{1}{x}+C$

d) $\int \left(2^x+\frac{3}{x^2}\right)dx$$=\int 2^{x}dx+3\int x^{-2}dx$$=\frac{2^x}{\ln 2}-\frac{3}{x}+C$

Bài 4.4 trang 11 Toán 12 Tập 2: Tìm:

a) $\int \left(2\cos x-\frac{3}{{\sin }^{2}x}\right)dx$; b) $\int 4{\sin }^2\frac{x}{2}dx$;

c) $\int {\left(\sin \frac{x}{2}-\cos \frac{x}{2}\right)}^{2}dx$; d) $\int \left(x+{\tan }^{2}x\right)dx$

Lời giải:

a) $\int \left(2\cos x-\frac{3}{{\sin }^{2}x}\right)dx$$=2\int \cos xdx-3\int \frac{1}{{\sin }^{2}x}dx$$=2\sin x+3\cot x+C$

b) $\int 4{\sin }^2\frac{x}{2}dx$$=2\int \left(1-\cos x\right)dx$$=2\int dx-2\int \cos xdx$$=2x-2\sin x+C$

c) $\int {\left(\sin \frac{x}{2}-\cos \frac{x}{2}\right)}^{2}dx$$=\int \left(1-2\sin \frac{x}{2}\cos \frac{x}{2}\right)dx$$=\int dx-\int \sin xdx$$=x+\cos x+C$

d) $\int \left(x+{\tan }^{2}x\right)dx$$=\int xdx+\int \left(\frac{1}{{\cos }^{2}x}-1\right)dx$

$=\int xdx+\int \frac{1}{{\cos }^{2}x}dx-\int dx$$=\frac{x^2}{2}+\tan x-x+C$

Bài 4.5 trang 11 Toán 12 Tập 2: Cho hàm số y = f(x) xác định trên khoảng (0; +∞). Biết rằng, $f^{\text{'}}\left(x\right)=2x+\frac{1}{x^2}$ với mọi x ∈ (0; +∞) và f(1) = 1. Tính giá trị f(4).

Lời giải:

Có $f\left(x\right)=\int f^{\text{'}}\left(x\right)dx=\int \left(2x+\frac{1}{x^2}\right)dx=x^2-\frac{1}{x}+C$

Vì f(1) = 1 nên 1 – 1 + C = 1 Þ C = 1.

Do đó $f\left(x\right)=x^2-\frac{1}{x}+1$

Vậy $f\left(4\right)=4^2-\frac{1}{4}+1=\frac{67}{4}$

Bài 4.6 trang 11 Toán 12 Tập 2: Cho hàm số y = f(x) có đồ thị là (C). Xét điểm M(x; f(x)) thay đổi trên (C). Biết rằng, hệ số góc của tiếp tuyến của đồ thị (C) tại M là k_M = (x – 1)² và điểm M trùng với gốc tọa độ khi nó nằm trên trục tung. Tìm biểu thức f(x).

Lời giải:

Vì hệ số góc của tiếp tuyến của đồ thị (C) tại M là k_M = (x – 1)² nên ta có:

$f\left(x\right)=\int {\left(x-1\right)}^{2}dx=\int \left(x^2-2x+1\right)dx$$=\int x^{2}dx-2\int xdx+\int dx$$=\frac{x^3}{3}-x^2+x+C$

Vì điểm M trùng với gốc tọa độ khi nó nằm trên trục tung nên f(0) = 0.

Do đó $f\left(0\right)=\frac{0^3}{3}-0^2+0+C=0\Rightarrow C=0$

Do đó $f\left(x\right)=\frac{x^3}{3}-x^2+x$

Bài 4.7 trang 11 Toán 12 Tập 2: Một viên đạn được bắn thẳng đứng lên trên từ mặt đất. Giả sử tại thời điểm t giây (coi t = 0 là thời điểm viên đạn được bắn lên), vận tốc của nó được cho bởi v(t) = 160 – 9,8t (m/s). Tìm độ cao của viên đạn (tính từ mặt đất):

a) Sau t = 5 giây;

b) Khi nó đạt độ cao lớn nhất (làm tròn kết quả đến chữ số thập phân thứ nhất).

Lời giải:

Gọi S(t) là độ cao của viên đạn bắn lên từ mặt đất sau t giây kể từ thời điểm đạn được bắn lên.

Khi đó $S\left(t\right)=\int v\left(t\right)dt=\int \left(160-\mathrm{9,8}t\right)dt=160t-\mathrm{4,9}{t}^2+C$

Vì S(0) = 0 nên 160.0 – 4,9.0 + C = 0 => C = 0.

Do đó S(t) = −4,9t² + 160 t.

a) Sau 5 giây độ cao của viên đạn là: S(5) = −4,9.5² + 160.5 = 677,5 (m).

b) Có S(t) = −4,9t² + 160t

$-\frac{1}{10}\left(49t^2-2.7t.\frac{800}{7}+\frac{640000}{49}\right)+\frac{64000}{49}$

$-\frac{1}{10}{\left(7t-\frac{800}{7}\right)}^2+\frac{64000}{49}\le \frac{64000}{49}$

Viên đạn đạt độ cao lớn nhất là $\frac{64000}{49}\approx \mathrm{1306,1}$m khi $t=\frac{800}{49}$giây.