Toán 12 Bài 3 (Kết nối tri thức): Đường tiệm cận của đồ thị hàm số

Với giải bài tập Toán lớp 12 Bài 3: Đường tiệm cận của đồ thị hàm số sách Kết nối tri thức hay nhất, chi tiết giúp học sinh dễ dàng làm bài tập Toán 12 Bài 3.

1 1,895 08/06/2024

Trang trước

Trang sau

Giải Toán 12 Bài 3: Đường tiệm cận của đồ thị hàm số

1. Đường tiệm cận ngang

Giải Toán 12 trang 20 Tập 1

HĐ1 trang 20 Toán 12 Tập 1: Cho hàm số $y = f (x) = \frac{2 x + 1}{x}$ có đồ thị (C). Với $x > 0$ , xét điểm M (x; f(x)) thuộc (C). Gọi H là hình chiếu vuông góc của M trên đường thẳng $y = 2$ (H.1.19).

a) Tính khoảng cách MH.

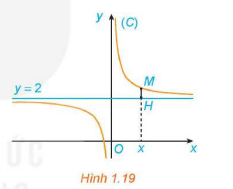
b) Có nhận xét gì về khoảng cách MH khi $x \to + \infty$ ?

Lời giải:

a) Ta có: $M (x; \frac{2 x + 1}{x})$ ; $H (x; 2)$ .

Do đó, $M H = \sqrt{{(x - x)}^{2} + {(2 - \frac{2 x + 1}{x})}^{2}} = \sqrt{{(\frac{2 x - 2 x - 1}{x})}^{2}} = \frac{1}{x}$ (do $x > 0$ )

b) Ta có: $lim_{x \to + \infty} \frac{1}{x} = 0$ . Do đó, khi $x \to + \infty$ thì $M H \to 0$ .

Giải Toán 12 trang 21 Tập 1

Luyện tập 1 trang 21 Toán 12 Tập 1: Tìm tiệm cận ngang của đồ thị hàm số $y = f (x) = \frac{2 x - 1}{x - 1}$ .

Lời giải:

Ta có: $lim_{x \to + \infty} \frac{2 x - 1}{x - 1} = lim_{x \to + \infty} \frac{2 - \frac{1}{x}}{1 - \frac{1}{x}} = 2; lim_{x \to - \infty} \frac{2 x - 1}{x - 1} = lim_{x \to - \infty} \frac{2 - \frac{1}{x}}{1 - \frac{1}{x}} = 2$ .

Do đó, tiệm cận ngang của đồ thị hàm số $y = f (x) = \frac{2 x - 1}{x - 1}$ là $y = 2$ .

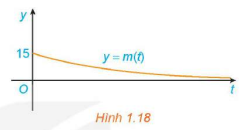
Vận dụng 1 trang 21 Toán 12 Tập 1: Giải bài toán trong tình huống mở đầu.

Giả sử khối lượng còn lại của một chất phóng xạ (gam) sau t ngày phân rã được cho bởi hàm số $m (t) = 15 e^{- 0, 012 t}$ . Khối lượng m(t) thay đổi ra sao khi $t \to + \infty$ ? Điều này thể hiện trên Hình 1.18 như thế nào?

Lời giải:

Ta có: $lim_{t \to + \infty} m (t) = lim_{t \to + \infty} 15 e^{- 0, 012 t} = lim_{t \to + \infty} \frac{15}{e^{0, 012 t}} = 0$

Do đó, $m (t) \to 0$ khi $t \to + \infty$ .

Trong hình 1.18, khi $t \to + \infty$ thì m(t) càng gần trục hoành Ot (nhưng không chạm trục Ot).

2. Đường tiệm cận đứng

HĐ2 trang 21 Toán 12 Tập 1: Cho hàm số $y = f (x) = \frac{x}{x - 1}$ có đồ thị (C). Với $x > 1$ , xét điểm M (x; f(x)) thuộc (C). Gọi H là hình chiếu vuông góc của M trên đường thẳng $x = 1$ (H.1.22).

a) Tính khoảng cách MH.

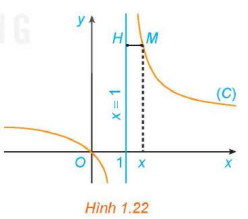
b) Khi M thay đổi trên (C) sao cho khoảng cách MH dần đến 0, có nhận xét gì về tung độ của điểm M?

Lời giải:

a) Ta có: $M (x; \frac{x}{x - 1}); H (1; \frac{x}{x - 1})$

Do đó, $M H = \sqrt{{(1 - x)}^{2} + {(\frac{x}{x - 1} - \frac{x}{x - 1})}^{2}} = x - 1$ (do $x > 1$ )

b) Khi khoảng cách MH dần đến 0 thì tung độ của điểm M dần ra xa vô tận về phía trên (tung độ điểm M tiến ra $+ \infty$ ).

Giải Toán 12 trang 22 Tập 1

Luyện tập 2 trang 22 Toán 12 Tập 1: Tìm các tiệm cận ngang và tiệm cận đứng của đồ thị hàm số $y = f (x) = \frac{2 x + 1}{x - 4}$ .

Lời giải:

Ta có: $lim_{x \to + \infty} \frac{2 x + 1}{x - 4} = lim_{x \to + \infty} \frac{2 + \frac{1}{x}}{1 - \frac{4}{x}} = 2; lim_{x \to - \infty} \frac{2 x + 1}{x - 4} = lim_{x \to - \infty} \frac{2 + \frac{1}{x}}{1 - \frac{4}{x}} = 2$ nên tiệm cận ngang của đồ thị hàm số $y = f (x) = \frac{2 x + 1}{x - 4}$ là $y = 2$ .

Lại có: $lim_{x \to 4^{+}} f (x) = lim_{x \to 4^{+}} \frac{2 x + 1}{x - 4} = + \infty; lim_{x \to 4^{-}} f (x) = lim_{x \to 4^{-}} \frac{2 x + 1}{x - 4} = - \infty$ nên tiệm cận đứng của đồ thị hàm số $y = f (x) = \frac{2 x + 1}{x - 4}$ đường thẳng $x = 4$ .

Vận dụng 2 trang 22 Toán 12 Tập 1: Để loại bỏ p% một loài tảo độc khỏi hồ nước, người ta ước tính chi phí bỏ ra là $C (p) = \frac{45 p}{100 - p}$ (triệu đồng), với $0 \leq p < 100$ . Tìm tiệm cận đứng của đồ thị hàm số C(p) và nêu ý nghĩa của đường tiệm cận này.

Lời giải:

Ta có: $lim_{p \to 100^{-}} C (p) = lim_{p \to 100^{-}} \frac{45 p}{100 - p} = + \infty$ nên tiệm cận đứng của đồ thị hàm số C(p) là $p = 100$ .

Ý nghĩa của đường tiệm cận là: Không thể loại bỏ hết loài tảo độc ra khỏi hồ nước dù chi phí là bao nhiêu.

3. Đường tiệm cận xiên

Giải Toán 12 trang 23 Tập 1

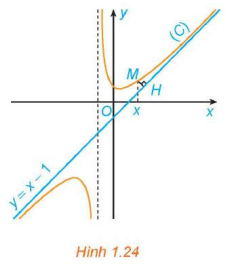
HĐ3 trang 23 Toán 12 Tập 1: Cho hàm số $y = f (x) = x - 1 + \frac{2}{x + 1}$ có đồ thị (C) và đường thẳng $y = x - 1$ như Hình 1.24.

a) Với $x > - 1$ , xét điểm M (x; f(x)) thuộc (C). Gọi H là hình chiếu vuông góc của M trên đường thẳng $y = x - 1$ . Có nhận xét gì về khoảng cách MH khi $x \to + \infty$ ?

b) Chứng tỏ rằng $lim_{x \to + \infty} [f (x) - (x - 1)] = 0$ . Tính chất này thể hiện trên Hình 1.24 như thế nào?

Lời giải:

a) Nhìn vào đồ thị ta thấy, khi $x \to + \infty$ thì khoảng cách MH tiến tới 0.

b) Ta có: $lim_{x \to + \infty} [f (x) - (x - 1)] = lim_{x \to + \infty} [x - 1 + \frac{2}{x + 1} - (x - 1)] = lim_{x \to + \infty} \frac{2}{x + 1} = lim_{x \to + \infty} \frac{\frac{2}{x}}{1 + \frac{1}{x}} = 0$

Tính chất này được thể hiện trong Hình 1.24 là: Khoảng cách từ điểm M của đồ thị hàm số (C) đến đường thẳng $y = x - 1$ tiến đến 0 khi $x \to + \infty$ .

Giải Toán 12 trang 24 Tập 1

Luyện tập 3 trang 24 Toán 12 Tập 1: Tìm các tiệm cận đứng và tiệm cận xiên của đồ thị hàm số $y = f (x) = \frac{x^{2} - 4 x + 2}{1 - x}$ .

Lời giải:

Ta có: $lim_{x \to 1^{+}} f (x) = lim_{x \to 1^{+}} \frac{x^{2} - 4 x + 2}{1 - x} = + \infty$ ; $lim_{x \to 1^{-}} f (x) = lim_{x \to 1^{-}} \frac{x^{2} - 4 x + 2}{1 - x} = - \infty$

Vậy tiệm cận đứng của đồ thị hàm số $y = f (x)$ là đường thẳng $x = 1$

Ta có: $y = f (x) = \frac{x^{2} - 4 x + 2}{1 - x} = - x + 3 - \frac{1}{1 - x}$

Do đó, $lim_{x \to + \infty} [f (x) - (- x + 3)] = lim_{x \to + \infty} \frac{- 1}{1 - x} = 0$ , $lim_{x \to - \infty} [f (x) - (- x + 3)] = lim_{x \to - \infty} \frac{- 1}{1 - x} = 0$

Vậy tiệm cận xiên của đồ thị hàm số $y = f (x)$ là đường thẳng $y = - x + 3$

Bài tập

Giải Toán 12 trang 25 Tập 1

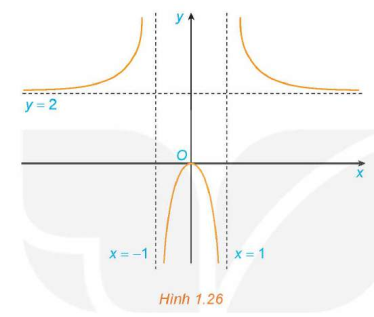
Bài 1.16 trang 25 Toán 12 Tập 1: Hình 1.26 là đồ thị của hàm số $y = f (x) = \frac{2 x^{2}}{x^{2} - 1}$

Sử dụng đồ thị này, hãy:
a) Viết kết quả của các giới hạn sau: $lim_{x \to - \infty} f (x)$ ; $lim_{x \to + \infty} f (x)$ ; $lim_{x \to 1^{-}} f (x)$ ; $lim_{x \to - 1^{+}} f (x)$
b) Chỉ ra các tiệm cận của đồ thị hàm số đã cho.

Lời giải:

a) $lim_{x \to - \infty} f (x) = 2$ ; $lim_{x \to + \infty} f (x) = 2$ ; $lim_{x \to 1^{-}} f (x) = - \infty$ ; $lim_{x \to - 1^{+}} f (x) = - \infty$

b) Do đó, tiệm cận đứng của đồ thị hàm số là $x = 1; x = - 1$ .

Tiệm cận ngang của đồ thị hàm số là $y = 2$

Bài 1.17 trang 25 Toán 12 Tập 1: Đường thẳng

x = 1

có phải là tiệm cận đứng của đồ thị hàm số

y = \frac{x^{2} + 2 x - 3}{x - 1}

không?

Lời giải:

Ta có: $lim_{x \to 1^{+}} f (x) = lim_{x \to 1^{+}} \frac{x^{2} + 2 x - 3}{x - 1} = lim_{x \to 1^{+}} \frac{(x - 1) (x + 3)}{x - 1} = lim_{x \to 1^{+}} (x + 3) = 4$

$lim_{x \to 1^{-}} f (x) = lim_{x \to 1^{-}} \frac{x^{2} + 2 x - 3}{x - 1} = lim_{x \to 1^{-}} \frac{(x - 1) (x + 3)}{x - 1} = lim_{x \to 1^{-}} (x + 3) = 4$

Do đó, đường thẳng $x = 1$ không là tiệm cận đứng của đồ thị hàm số $y = \frac{x^{2} + 2 x - 3}{x - 1}$ .

Bài 1.18 trang 25 Toán 12 Tập 1: Tìm các tiệm cận của đồ thị hàm số sau:
a) $y = \frac{3 - x}{2 x + 1}$ ;
b) $y = \frac{2 x^{2} + x - 1}{x + 2}$ .

Lời giải:

a) Vì $lim_{x \to + \infty} y = lim_{x \to + \infty} \frac{3 - x}{2 x + 1} = lim_{x \to + \infty} \frac{\frac{3}{x} - 1}{2 + \frac{1}{x}} = - \frac{1}{2}$ ;

$lim_{x \to - \infty} y = lim_{x \to - \infty} \frac{3 - x}{2 x + 1} = lim_{x \to - \infty} \frac{\frac{3}{x} - 1}{2 + \frac{1}{x}} = - \frac{1}{2}$

Do đó, đường thẳng $y = \frac{- 1}{2}$ là tiệm cận ngang của đồ thị hàm số $y = \frac{3 - x}{2 x + 1}$ .

Vì $lim_{x \to {(- \frac{1}{2})}^{-}} y = lim_{x \to {(- \frac{1}{2})}^{-}} \frac{3 - x}{2 x + 1} = - \infty; lim_{x \to {(- \frac{1}{2})}^{+}} y = lim_{x \to {(- \frac{1}{2})}^{+}} \frac{3 - x}{2 x + 1} = + \infty$

Do đó, đường thẳng $x = \frac{- 1}{2}$ là tiệm cận đứng của đồ thị hàm số $y = \frac{3 - x}{2 x + 1}$ .

b) Vì $lim_{x \to - \infty} y = lim_{x \to - \infty} \frac{2 x^{2} + x - 1}{x + 2} = lim_{x \to - \infty} [x \frac{(2 + \frac{1}{x} - \frac{1}{x^{2}})}{(1 + \frac{2}{x})}] = - \infty$

$lim_{x \to + \infty} y = lim_{x \to + \infty} \frac{2 x^{2} + x - 1}{x + 2} = lim_{x \to + \infty} [x \frac{(2 + \frac{1}{x} - \frac{1}{x^{2}})}{(1 + \frac{2}{x})}] = + \infty$

Do đó, đồ thị hàm số $y = \frac{2 x^{2} + x - 1}{x + 2}$ không có tiệm cận ngang.

Vì $lim_{x \to - 2^{-}} y = lim_{x \to - 2^{-}} \frac{2 x^{2} + x - 1}{x + 2} = - \infty; lim_{x \to - 2^{+}} y = lim_{x \to - 2^{+}} \frac{2 x^{2} + x - 1}{x + 2} = + \infty$

Do đó, đồ thị hàm số $y = \frac{2 x^{2} + x - 1}{x + 2}$ có tiệm cận đứng là $x = - 2$

Ta có: $y = \frac{2 x^{2} + x - 1}{x + 2} = 2 x - 3 + \frac{5}{x + 2}$

$lim_{x \to + \infty} [f (x) - (2 x - 3)] = lim_{x \to + \infty} [2 x - 3 + \frac{5}{x + 2} - (2 x - 3)] = lim_{x \to + \infty} \frac{5}{x + 2} = 0$

$lim_{x \to - \infty} [f (x) - (2 x - 3)] = lim_{x \to - \infty} [2 x - 3 + \frac{5}{x + 2} - (2 x - 3)] = lim_{x \to - \infty} \frac{5}{x + 2} = 0$

Do đó, đồ thị hàm số $y = \frac{2 x^{2} + x - 1}{x + 2}$ có tiệm cận xiên là: $y = 2 x - 3$ .

Bài 1.19 trang 25 Toán 12 Tập 1: Một công ty sản xuất đồ gia dụng ước tính chi phí để sản xuất x (sản phẩm) là $C (x) = 2 x + 50$ (triệu đồng). Khi đó, $f (x) = \frac{C (x)}{x}$ là chi phí sản xuất trung bình cho mỗi sản phẩm. Chứng tỏ rằng hàm số f(x) giảm và $lim_{x \to + \infty} f (x) = 2$ . Tính chất này nói lên điều gì?

Lời giải:

Ta có: $f (x) = \frac{C (x)}{x} = \frac{2 x + 50}{x}$

Vì $f^{'} (x) = \frac{- 50}{x^{2}} < 0$ với mọi số thực x nên hàm số $f (x) = \frac{C (x)}{x}$ giảm.

$lim_{x \to + \infty} f (x) = lim_{x \to + \infty} \frac{2 x + 50}{x} = lim_{x \to + \infty} \frac{2 + \frac{50}{x}}{1} = 2$ (đpcm)

Tính chất này nói lên: Khi sản xuất càng nhiều sản phẩm thì chi phí sản xuất trung bình cho mỗi sản phẩm càng giảm, nhưng không dưới 2.

Bài 1.20 trang 25 Toán 12 Tập 1: Một mảnh vườn hình chữ nhật có diện tích bằng $144 m^{2}$ . Biết độ dài một cạnh của mảnh vườn là x (m).

a) Viết biểu thức tính chu vi P(x) (mét) của mảnh vườn.

b) Tìm các tiệm cận của đồ thị hàm số P(x).

Lời giải:

a) Độ dài cạnh còn lại của mảnh vườn là: $\frac{144}{x} (m)$

Chu vi của mảnh vườn là: $P (x) = 2 (x + \frac{144}{x}) = 2 x + \frac{288}{x} (m)$

b) Vì $lim_{x \to + \infty} P (x) = lim_{x \to + \infty} (2 x + \frac{288}{x}) = + \infty$ ; $lim_{x \to - \infty} P (x) = lim_{x \to - \infty} (2 x + \frac{288}{x}) = - \infty$

Do đó, đồ thị hàm số P(x) không có tiệm cận ngang.

Vì $lim_{x \to 0^{-}} y = lim_{x \to 0^{-}} (2 x + \frac{288}{x}) = - \infty; lim_{x \to 0^{+}} y = lim_{x \to 0^{+}} (2 x + \frac{288}{x}) = + \infty$

Do đó, đồ thị hàm số P(x) có tiệm cận đứng là $x = 0$ .

Ta có: $lim_{x \to + \infty} [P (x) - 2 x] = lim_{x \to + \infty} (2 x + \frac{288}{x} - 2 x) = lim_{x \to + \infty} \frac{288}{x} = 0$

Do đó, đồ thị hàm số P(x) có tiệm cận xiên là: $y = 2 x$ .

Xem thêm các bài giải sách giáo khoa Toán 12 bộ sách Kết nối tri thức hay, chi tiết khác:

Bài 2: Giá trị lớn nhất và giá trị nhỏ nhất của hàm số

Bài 4: Khảo sát sự biến thiên và vẽ đồ thị của hàm số

Bài 5: Ứng dụng đạo hàm để giải quyết một số vấn đề liên quan đến thực tiễn

Bài tập cuối chương 1 trang 42

Bài 6: Vectơ trong không gian

1 1,895 08/06/2024

Trang trước

Trang sau

Xem thêm các chương trình khác:

Lớp 1 - Cánh diều

Tiếng Anh 1

Toán lớp 1

Tiếng Việt lớp 1

Lớp 1 - Chân trời sáng tạo

Tiếng Anh 1

Toán lớp 1

Tiếng Việt lớp 1

Lớp 1 - Kết nối tri thức

Tiếng Anh 1

Toán lớp 1

Tiếng Việt lớp 1

Tiện ích

Đọc sách online

Bộ đề ôn hè lớp 1 lên lớp 2

Giáo án lớp 1

Lớp 2 - Kết nối tri thức

Toán lớp 2

Tiếng Việt lớp 2

Đạo đức lớp 2

Tự nhiên và Xã hội lớp 2

Hoạt động trải nghiệm lớp 2

Tiếng Anh lớp 2

Âm nhạc lớp 2

Lớp 2 - Cánh diều

Toán lớp 2

Tiếng Việt lớp 2

Hoạt động trải nghiệm lớp 2

Tự nhiên và Xã hội lớp 2

Tiếng Anh lớp 2

Âm nhạc lớp 2

Đạo đức lớp 2

Lớp 2 - Chân trời sáng tạo

Toán lớp 2

Tiếng Việt lớp 2

Đạo đức lớp 2

Tự nhiên và Xã hội lớp 2

Hoạt động trải nghiệm lớp 2

Tiếng Anh lớp 2

Âm nhạc lớp 2

Đề thi các môn lớp 2

Đề thi các môn lớp 2 - Kết nối tri thức

Đề thi các môn lớp 2 - Cánh diều

Đề thi các môn lớp 2 - Chân trời sáng tạo

Tiện ích

Đọc sách online

Bộ đề ôn hè lớp 2 lên lớp 3

Giáo án lớp 2

Lớp 3 - Kết nối tri thức

Toán lớp 3

Tiếng Anh lớp 3

Tiếng Việt lớp 3

Đạo đức lớp 3

Tự nhiên và Xã hội lớp 3

Hoạt động trải nghiệm lớp 3

Âm nhạc lớp 3

Tin học lớp 3

Giáo dục thể chất lớp 3

Công nghệ lớp 3

Lớp 3 - Cánh diều

Toán lớp 3

Tiếng Việt lớp 3

Tiếng Anh lớp 3

Đạo đức lớp 3

Tự nhiên và Xã hội lớp 3

Hoạt động trải nghiệm lớp 3

Âm nhạc lớp 3

Tin học lớp 3

Giáo dục thể chất lớp 3

Công nghệ lớp 3

Lớp 3 - Chân trời sáng tạo

Toán lớp 3

Tiếng Việt lớp 3

Tiếng Anh lớp 3

Đạo đức lớp 3

Tự nhiên và Xã hội lớp 3

Hoạt động trải nghiệm lớp 3

Âm nhạc lớp 3

Tin học lớp 3

Giáo dục thể chất lớp 3