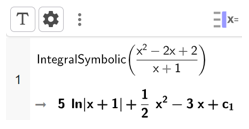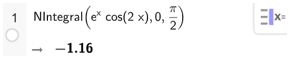Nội dung bài viết

    Xem thêm

    Giải Toán 12 (Kết nối tri thức): Tính nguyên hàm và tích phân với phần mềm GeoGebra. Tính gần đúng tích phân bằng phương pháp hình thang

    Với giải bài tập Toán lớp 12 Tính nguyên hàm và tích phân với phần mềm GeoGebra. Tính gần đúng tích phân bằng phương pháp hình thang sách Kết nối tri thức hay nhất, chi tiết giúp học sinh dễ dàng làm bài tập Toán 12.

    1 605 10/07/2026
    Trang trước
    Chia sẻ
    Trang sau  

    Giải Toán 12 Tính nguyên hàm và tích phân với phần mềm GeoGebra. Tính gần đúng tích phân bằng phương pháp hình thang

    Thực hành 1 trang 82 Toán 12 Tập 2: Sử dụng phần mềm Geogebra, tính:

    a) ∫x2−2x+2x+1dx

    b) ∫0π2excos2xdx

    Lời giải:

    Khởi động phần mềm Geogebra, chọn Complex Adaptive System (CAS) để thực hiện tính toán nguyên hàm và tích phân.

    a) Để tính ∫x2−2x+2x+1dx, ta dùng lệnh IntegralSymbolic(x2−2x+2x+1), kết quả sẽ được hiển thị ngay bên dưới như hình sau:

    Thực hành 1 trang 82 Toán 12 Tập 2 | Kết nối tri thức Giải Toán 12

    Vậy ∫x2−2x+2x+1dx = 5ln|x + 1| + 12x2 – 3x + C.

    b) Để tính gần đúng tích phân ∫0π2excos2xdx, ta dùng lệnh Nintegral(excos2x, 0, π2), kết quả sẽ được hiển thị ngay bên dưới như hình sau:

    Thực hành 1 trang 82 Toán 12 Tập 2 | Kết nối tri thức Giải Toán 12

    Vậy ∫0π2excos2xdx ≈ – 1,16.

    Thực hành 2 trang 84 Toán 12 Tập 2: Sử dụng phương pháp hình thang, tính gần đúng ∫12exx dx với độ chính xác 0,01.

    Lời giải:

    1. Ta có: fx=exx

    f'x=exx'=ex⋅x−exx2=1x−1x2 ex;

     f''x=1x−1x2 ex'=1x−2x2+2x3ex

    f'''x=1x−2x2+2x3ex'=1x−3x2+6x3−6x4ex

    f'''(x) = 0 thì x ≈ 1,596.

    Ta có f''(1) = e; f''(1,596) ≈ 0,333 ∙ e1,569; f''(2) = e24

    Do đó, M=maxx∈1;2f''x=e

    2. Ta cần tìm n sao cho:

    2−13⋅e12n2<0,01⇔e12n2<0,01⇔n>25e3.

    Do đó, ta chọn n = 5.

    3. Chia đoạn [1; 2] thành 5 đoạn có độ dài bằng nhau là [1; 1,2], [1,2; 1,4], [1,4; 1,6], [1,6; 1,8], [1,8; 2].

    Áp dụng công thức hình thang, ta có:

    ∫12exxdx≈2−12⋅5e11+2⋅e1,21,2+2⋅e1,41,4+2⋅e1,61,6+2⋅e1,81,8+e22≈ 3,065.

    Vận dụng trang 84 Toán 12 Tập 2: Một thân cây dài 4,8 m được cắt thành các khúc gỗ dài 60 cm. Người ta đo đường kính của mỗi mặt cắt ngang và diện tích S của nó được ghi lại trong bảng dưới đây, ở đây x (cm) là khoảng cách tính từ đỉnh thân cây đến vết cắt.

    x (cm)

    0

    60

    120

    180

    240

    300

    360

    420

    480

    S (cm2)

    240

    248

    256

    260

    264

    272

    298

    316

    320

    Tìm thể tích gần đúng của thân cây này.

    Hướng dẫn.

    Thể tích cần tính là V=∫0480Sxdx, trong đó S(x) là diện tích mặt cắt ngang tại vị trí cách đỉnh thân cây một khoảng x (cm). Sử dụng phương pháp hình thang để tính gần đúng tích phân này.

    Lời giải:

    Thể tích gần đúng của thân cây đã cho là V=∫0480Sxdx

    Ta chia đoạn [0; 480] thành n = 8 đoạn con có độ dài bằng nhau, mỗi đoạn có độ dài là 60. Các đoạn đó là: [0; 60], [60; 120], [120; 180], [180; 240], [240; 300], [300; 360], [360; 420], [420; 480].

    Áp dụng công thức hình thang, ta có:

    V=∫0480Sxdx≈480−02⋅8 (240 + 2 ∙ 248 + 2 ∙ 256 + 2 ∙ 260 + 2 ∙ 264 + 2 ∙ 272 + 2 ∙ 298 + 2.316 + 320] = 131 640 (cm3) = 0,13164 (m3­).

    Xem thêm lời tài liệu Toán lớp 12 Kết nối tri thức với cuộc sống hay, chi tiết khác:

    Giáo án điện tử Tính nguyên hàm và tích phân với phần mềm GeoGebra. Tính gần đúng tích phân bằng phương pháp hình thang lớp 12

    Giáo án Tính nguyên hàm và tích phân với phần mềm GeoGebra. Tính gần đúng tích phân bằng phương pháp hình thang lớp 12

    Tham khảo các loạt bài Toán 12 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 605 10/07/2026
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: