Nội dung bài viết

    Xem thêm

    Xét chiều biến thiên và tìm các cực trị (nếu có) của các hàm số sau: a) y = x^3 - 3x^2 + 3x - 1

    Lời giải Bài 1.40 trang 43 Toán 12 Tập 1 sách Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 12.

    1 1,005 09/06/2024
    Trang trước
    Chia sẻ
    Trang sau  

    Giải Toán 12 Kết nối tri thức Bài tập cuối chương 1 trang 42

    Bài 1.40 trang 43 Toán 12 Tập 1: Xét chiều biến thiên và tìm các cực trị (nếu có) của các hàm số sau:

    a) y=x3−3x2+3x−1;

    b) y=x4−2x2−1;

    c) y=2x−13x+1;

    d) y=x2+2x+2x+1.

    Lời giải:

    a) Tập xác định: D=R.

    Ta có: y′=3x2−6x+3=3(x−1)2,y′=0⇔x=1

    Lập bảng biến thiên của hàm số:

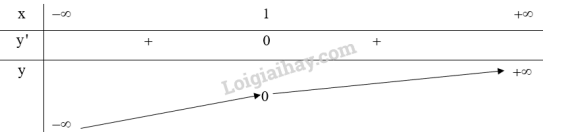
    Tài liệu VietJack

    Hàm số y=x3−3x2+3x−1 đồng biến trên khoảng (−∞;1) và (1;+∞).

    Hàm số y=x3−3x2+3x−1 không có cực trị.

    b) Tập xác định của hàm số là D=R.

    Ta có: y′=4x3−4x,y′=0⇔4x3−4x=0⇔[x=0x=±1

    Bảng biến thiên:

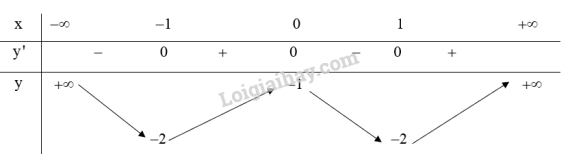
    Tài liệu VietJack

    Từ bảng biến thiên ta có:

    Hàm số y=x4−2x2−1 đồng biến trên khoảng (−1;0) và (1;+∞).

    Hàm số y=x4−2x2−1 nghịch biến trên khoảng (−∞;−1) và (0;1).

    Hàm số y=x4−2x2−1 đạt cực đại tại x=0 và .

    Hàm số y=x4−2x2−1 đạt cực tiểu tại x=±1 và yCT=−2.

    c) Tập xác định: D=R∖{−13}.

    Ta có: y′=2(3x+1)−3(2x−1)(3x+1)2=5(3x+1)2>0∀x≠−13

    Lập bảng biến thiên của hàm số:

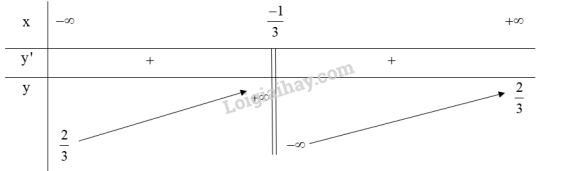
    Tài liệu VietJack

    Từ bảng biến thiên ta có:

    Hàm số y=2x−13x+1 đồng biến trên (−∞;−13) và (−13;+∞).

    Hàm số không có cực trị.

    d) Tập xác định: D=R∖{−1}.

    Ta có: y′=(2x+2)(x+1)−(x2+2x+2)(x+1)2=x2+2x(x+1)2

    y′=0⇔[x=0x=−2 (thỏa mãn)

    Lập bảng biến thiên của hàm số:

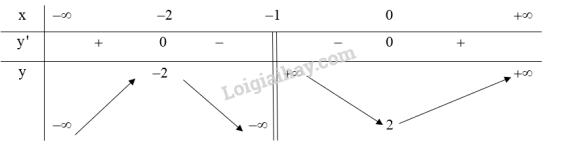
    Tài liệu VietJack

    Từ bảng biến thiên ta có:

    Hàm số y=x2+2x+2x+1 đồng biến trên khoảng (−∞;−2) và (0;+∞).

    Hàm số y=x2+2x+2x+1 nghịch biến trên khoảng (−2;−1) và (−1;0).

    Hàm số y=x2+2x+2x+1 đạt cực đại tại x=−2 và .

    Hàm số y=x2+2x+2x+1 đạt cực tiểu tại x=0 và yCT=2.

    Xem thêm các bài giải sách giáo khoa Toán 12 bộ sách Kết nối tri thức hay, chi tiết khác:

    Bài 1.30 trang 42 Toán 12 Tập 1: Cho hàm số y=f(x) có đạo hàm trên khoảng (a; b). Phát biểu nào dưới đây là đúng?...

    Bài 1.31 trang 42 Toán 12 Tập 1: Hàm số nào sau đây nghịch biến trên R? A. y=−x3+3x2−9x; B. y=−x3+x+1;...

    Bài 1.33 trang 42 Toán 12 Tập 1: Hàm số nào dưới đây không có cực trị? A. y=|x|. B. y=x4...

    Bài 1.33 trang 42 Toán 12 Tập 1: Giá trị cực tiểu của hàm số y=x2ln⁡x là A. 1e. B. −1e...

    Bài 1.35 trang 42 Toán 12 Tập 1: Cho hàm số y=f(x) thỏa mãn: limx→2+⁡f(x)=1;limx→2−⁡f(x)=1;limx→−∞⁡f(x)=2 và limx→+∞⁡f(x)=2. Khẳng định nào sau đây là đúng?...

    Bài 1.36 trang 42 Toán 12 Tập 1: Tiệm cận xiên của đồ thị hàm số y=x2+2x−2x+2 là A. y=−2. B. y=1...

    Bài 1.37 trang 43 Toán 12 Tập 1: Cho hàm số y=f(x) xác định trên R∖{1;3}, liên tục trên mỗi khoảng xác định và có bảng biến thiên như sau...

    Bài 1.38 trang 43 Toán 12 Tập 1: Đồ thị trong Hình 1.37 là đồ thị của hàm số...

    Bài 1.39 trang 43 Toán 12 Tập 1: Đồ thị trong Hình 1.38 là đồ thị của hàm số...

    Bài 1.40 trang 43 Toán 12 Tập 1: Xét chiều biến thiên và tìm các cực trị (nếu có) của các hàm số sau: a) y=x3−3x2+3x−1; b) y=x4−2x2−1;...

    Bài 1.41 trang 44 Toán 12 Tập 1: Tìm giá trị lớn nhất và giá trị nhỏ nhất (nếu có) của các hàm số sau: a) y=2x+13x−2 trên nửa khoảng [2;+∞);...

    Bài 1.42 trang 44 Toán 12 Tập 1: Tìm các tiệm cận của mỗi đồ thị hàm số sau: a) y=3x−2x+1; b) y=x2+2x−12x−1...

    Bài 1.43 trang 44 Toán 12 Tập 1: Khảo sát sự biến thiên và vẽ đồ thị của các hàm số sau: a) y=−x3+6x2−9x+12; b) y=2x−1x+1;...

    Xem thêm các bài giải sách giáo khoa Toán 12 bộ sách Kết nối tri thức hay, chi tiết khác:

    Bài 5: Ứng dụng đạo hàm để giải quyết một số vấn đề liên quan đến thực tiễn

    Bài 6: Vectơ trong không gian

    Bài 7: Hệ trục toạ độ trong không gian

    Bài 8: Tính đơn điệu và cực trị của hàm số

    Bài tập cuối chương 2 trang 73, 74

    Tham khảo các loạt bài Toán 12 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 1,005 09/06/2024
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: