TOP 20 câu Trắc nghiệm Các phép toán trên tập hợp (Chân trời sáng tạo 2024) có đáp án - Toán 10
Bộ 20 bài tập trắc nghiệm Toán lớp 10 Bài 3: Các phép toán trên tập hợp có đáp án đầy đủ các mức độ sách Chân trời sáng tạo giúp học sinh ôn luyện trắc nghiệm Toán 10 Bài 3.
Chỉ 150k mua trọn bộ Trắc nghiệm Toán lớp 10 Chân trời sáng tạo bản word (cả năm) có đáp án chi tiết:
B1: Gửi phí vào tài khoản 0711000255837 - NGUYEN THANH TUYEN - Ngân hàng Vietcombank (QR)
B2: Nhắn tin tới zalo Vietjack Official - nhấn vào đây để thông báo và nhận tài liệu.
Xem thử tài liệu tại đây: Link tài liệu
Trắc nghiệm Toán 10 Bài 3: Các phép toán trên tập hợp - Chân trời sáng tạo
I. Nhận biết
Câu 1. Kí hiệu A ∩ B nghĩa là:
A. Hợp của hai tập hợp A và B;
B. Giao của hai tập hợp A và B;
C. Hiệu của tập hợp A và tập hợp B;
D. Phần bù của tập hợp A trong tập hợp B.
Đáp án: B
Giải thích:
Hợp của hai tập hợp A và B được kí hiệu là A ∪ B.
Giao của hai tập hợp A và B được kí hiệu là A ∩ B.
Hiệu của A và B được kí hiệu là A \ B.
Cho A ⊂ B, khi đó phần bù của A trong B được kí hiệu là CBA.
Vậy ta chọn đáp án B.
Câu 2. Trong các khẳng định sau, khẳng định nào sai?
A. x ∈ A \ B Þ x ∈ A;
B. x ∈ CEA Þ x ∉ A;
C. x ∈ A \ B Þ x ∉ B;
D. x ∈ A ∩ B Þ x ∈ A hoặc x ∈ B.
Đáp án: D
Giải thích:
⦁ Ta có A \ B = {x | x ∈ A và x ∉ B}.
Do đó phương án A, C đúng.
⦁ Kí hiệu CEA dùng để chỉ phần bù của A trong E, với A ⊂ E.
Do đó nếu x ∈ CEA thì x ∉ A.
Vì vậy phương án B đúng.
⦁ Ta có A ∩ B = {x | x ∈ A và x ∈ B}.
Do đó phương án D sai.
Vậy ta chọn phương án D.
Câu 3. Cho A = {1; 2; 4; 5} và B = {–2; –1; 0; 1; 2}. Khi đó A ∪ B là tập hợp:
A. {1; 2};
B. {–2; –1; 0; 1; 2; 4; 5};
C. {4; 5};
D. {–2; –1; 0}.
Đáp án: B
Giải thích:
Với A = {1; 2; 4; 5} và B = {–2; –1; 0; 1; 2}.
Khi đó A ∪ B là hợp của tập hợp A và tập hợp B, gồm tất cả các phần tử thuộc A hoặc B.
Þ A ∪ B = {–2; –1; 0; 1; 2; 4; 5}.
Ta chọn phương án B.
Câu 4. Cho tập E = {2; 4; 6; 9}, F = {1; 2; 3; 4}. Tập nào sau đây bằng tập E \ F?
A. {1; 2; 3; 5};
B. {1; 3; 6; 9};
C. {6; 9};
D. {1}.
Đáp án: C
Giải thích:
Tập E \ F bao gồm các phần tử thuộc tập E nhưng không thuộc tập F.
Các phần tử thuộc E nhưng không thuộc F là: 6; 9.
Do đó E \ F = {6; 9}.
Vậy ta chọn phương án C.
Câu 5. Cho hai tập hợp U = {1; 2; 3; 4}, V = {1; 2}. Tập CUV là tập hợp nào sau đây?
A. {1; 2};
B. {1; 2; 3; 4};
C. {3; 4};
D. ∅.
Đáp án: C
Giải thích:
Với U = {1; 2; 3; 4}, V = {1; 2} ta thấy V ⊂ U.
Tập CUV (= U \ V) bao gồm các phần tử thuộc U nhưng không thuộc V.
Các phần tử thuộc U nhưng không thuộc V là: 3; 4.
Do đó CUV = {3; 4}.
Vậy ta chọn phương án C.
Câu 6. Cho A ≠ ∅. Trong các mệnh đề sau, mệnh đề nào sai?
A. A ∪ ∅ = ∅;
B. ∅ ∪ A = A;
C. ∅ ∪ ∅ = ∅;
D. A ∪ A = A.
Đáp án: A
Giải thích:
Phương án B, C, D đúng.
Phương án A sai. Sửa lại: A ∪ ∅ = A.
Vậy ta chọn phương án A.
Câu 7. Cho hai tập hợp A và B khác rỗng thỏa mãn A ⊂ B. Trong các mệnh đề sau, mệnh đề nào sai?
A. A ∩ B = A;
B. A \ B = ∅;
C. B \ A = B;
D. A ∪ B = B.
Đáp án: C
Giải thích:
Ta có sơ đồ Ven biểu diễn A ⊂ B như sau:
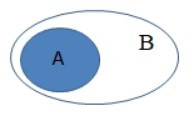
Quan sát sơ đồ Ven, ta thấy:
⦁ A ∩ B = A. Suy ra phương án A đúng.
⦁ A \ B = ∅. Suy ra phương án B đúng.
⦁ B \ A = CBA (phần không tô màu trên biểu đồ Ven). Suy ra phương án C sai.
⦁ A ∪ B = B. Suy ra phương án D đúng.
Vậy ta chọn phương án C.
II. Thông hiểu
Câu 1. Khẳng định nào sau đây sai?
A. ℤ ∪ ℚ = ℚ;
B. ℕ ∪ ℕ* = ℕ*;
C. ℚ ∩ ℝ = ℚ;
D. ℕ* ∩ ℝ = ℕ*.
Đáp án: B
Giải thích:
Ta có quan hệ bao hàm: ℕ* Ì ℕ Ì ℤ Ì ℚ Ì ℝ.
Khi đó:
• ℤ ∪ ℚ = ℚ. Do đó A đúng;
• ℕ ∪ ℕ* = ℕ. Do đó B sai;
• ℚ ∩ ℝ = ℚ. Do đó C đúng;
• ℕ* ∩ ℝ = ℕ*. Do đó D đúng.
Vậy ta chọn phương án B.
Câu 2. Cho tập hợp A = (–∞;–2] và tập B = (–1; +∞). Khi đó A ∪ B là:
A. (–2; +∞);
B. (–2; –1];
C. ℝ;
D. ∅.
Đáp án: C
Giải thích:
Để xác định tập hợp A ∪ B, ta vẽ sơ đồ sau đây:
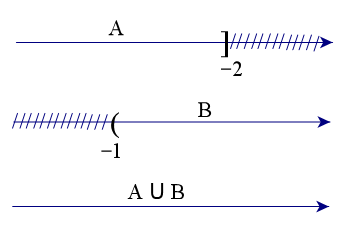
Từ sơ đồ, ta thấy A ∪ B = ℝ.
Vậy ta chọn phương án C.
Câu 3. Cho tập hợp C = [–5; 3), D = (1; +∞). Khi đó C ∩ D là tập nào sau đây?
A. (1; 3);
B. (1; 3];
C. [–5; +∞);
D. [–5; 1].
Đáp án: A
Giải thích:
Để xác định tập hợp C ∩ D, ta vẽ sơ đồ sau đây:
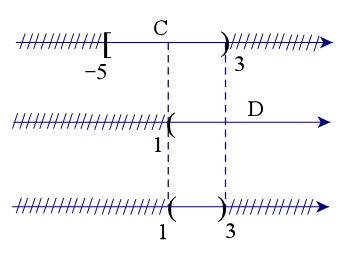
Từ sơ đồ, ta thấy C ∩ D = (1; 3).
Vậy ta chọn phương án A.
Câu 4. Cho hai tập hợp G = (1; 5]; H = (2; 7]. Tập hợp G \ H là:
A. (1; 2];
B. (2; 5);
C. (–1; 7];
D. (–1; 2).
Đáp án: A
Giải thích:
Để xác định tập hợp G \ H, ta vẽ sơ đồ sau đây:
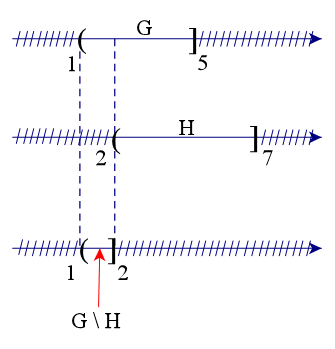
Từ sơ đồ, ta thấy G \ H = (1; 2] (vì tập H không lấy số 2 nên phần bù sẽ lấy số 2).
Vậy ta chọn phương án A.
Câu 5. Cho A, B, C là ba tập hợp được minh họa bằng biểu đồ Ven như hình vẽ.
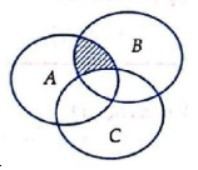
Phần gạch sọc trong hình vẽ là tập hợp nào sau đây?
A. (A ∪ B) \ C;
B. (A ∩ B) \ C;
C. (A \ C) ∪ (A \ B);
D. (A ∩ B) ∪ C.
Đáp án: B
Giải thích:
Quan sát hình vẽ, ta thấy mỗi phần tử x thuộc phần gạch sọc đều thỏa mãn cả 3 yêu cầu sau:
⦁ x ∈ A;
⦁ x ∈ B;
⦁ x ∉ C.
Vì x ∈ A và x ∈ B nên ta có x ∈ (A ∩ B).
Vì x ∈ (A ∩ B) và x ∉ C nên ta có x ∈ (A ∩ B) \ C.
Vậy ta chọn phương án B.
Câu 6. Cho hai tập hợp M = {1; 2; 4; 7; 9} và N = {–1; 0; 7; 10}. Tập hợp M \ N có bao nhiêu phần tử?
A. 1;
B. 2;
C. 3;
D. 4.
Đáp án: D
Giải thích:
Ta có M \ N là tập hợp gồm những phần tử thuộc M nhưng không thuộc N.
Do đó ta có các phần tử: 1; 2; 4; 9.
Vậy M \ N = {1; 2; 4; 9} có 4 phần tử.
Ta chọn phương án D.
Câu 7. Cho hai tập hợp A = {1; 2; a; b} và B = {1; x; y} với x, y khác a, b, 2, 1. Kết luận nào sau đây là đúng?
A. A ∩ B = B;
B. A ∩ B = ∅;
C. A ∩ B = A;
D. A ∩ B = {1}.
Đáp án: D
Giải thích:
Vì x, y khác a, b, 2, 1 nên A và B có một phần tử chung là 1.
Do đó A ∩ B = {1}.
Ta chọn phương án D.
Câu 8. Cho A: “Tập hợp các học sinh khối 10 học giỏi”, B: “Tập hợp các học sinh nữ khối 10 học giỏi”, C: “Tập hợp các học sinh nam khối 10 học giỏi”. Vậy tập hợp C là:
A. A ⊂ B;
B. B \ A;
C. A ∩ B;
D. A \ B.
Đáp án: D
Giải thích:
Vì tập hợp B là tập hợp các học sinh nữ khối 10 học giỏi nên tập hợp C gồm những phần tử thuộc tập hợp A mà không thuộc tập hợp B.
Do đó C = A \ B.
Ta chọn phương án D.
III. Vận dụng
Câu 1. Cho tập hợp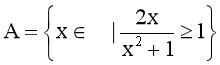 
; B là tập hợp tất cả các giá trị nguyên của b sao cho phương trình x2 – 2bx + 4 = 0 vô nghiệm. Số phần tử chung của hai tập hợp trên là:
A. 1;
B. 2;
C. 3;
D. 0.
Đáp án: A
Giải thích:
⦁ Xét tập hợp A:
Ta có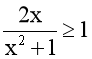 
.
Û 2x ≥ x2 + 1 (do x2 + 1 > 0)
Û x2 – 2x + 1 ≤ 0.
Û (x – 1)2 ≤ 0.
Mà (x – 1)2 ≥ 0 với mọi x.
Nên (x – 1)2 ≤ 0 Û x – 1 = 0
Û x = 1 ∈ ℝ.
Vì vậy A = {1}.
⦁ Xét tập hợp B:
Xét phương trình x2 – 2bx + 4 = 0 (*)
∆’ = b2 – 4.
Phương trình (*) vô nghiệm Û ∆’ < 0.
Û b2 – 4 < 0.
Û –2 < b < 2.
Vì b là số nguyên nên ta nhận b = –1; b = 0; b = 1.
Suy ra tập B = {–1; 0; 1}.
Tập A ∩ B = {1}.
Vậy số phần tử chung của tập A và tập B là 1 phần tử.
Do đó ta chọn phương án A.
Câu 2. Cho ba tập hợp A = [–2; 2], B = [1; 5], C = [0; 1]. Khi đó tập (A \ B) ∩ C là:
A. {0; 1};
B. [0; 1);
C. (–2; 1);
D. [–2; 5].
Đáp án: B
Giải thích:
Để xác định tập hợp A \ B, ta vẽ sơ đồ sau đây:
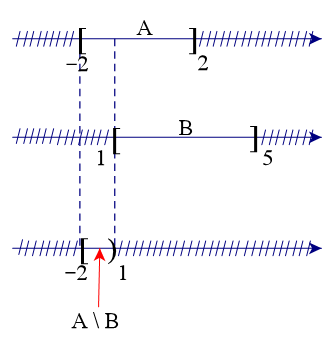
Từ sơ đồ, ta thấy A \ B = [–2; 1) (vì tập B chứa số 1 nên phần bù sẽ không lấy số 1).
Để xác định tập hợp (A \ B) ∩ C, ta vẽ sơ đồ sau đây:
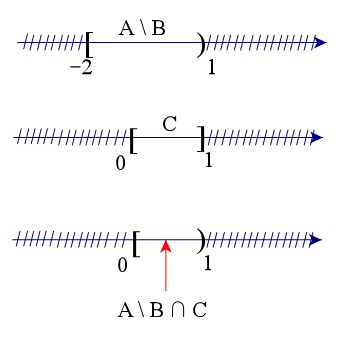
Từ sơ đồ, ta thấy (A \ B) ∩ C = [0; 1) (giao tức là lấy phần chung, tuy tập C có số 1 nhưng vì tập A \ B không lấy số 1 nên ta không lấy số 1).
Vậy ta chọn phương án B.
Câu 3. Cho A = {x ∈ ℝ | x + 2 ≥ 0}, B = {x ∈ ℝ | 5 – x ≥ 0}. Khi đó A \ B là:
A. [–2; 5];
B. [–2; 6];
C. (5; +∞);
D. (2; +∞).
Đáp án: C
Giải thích:
⦁ Ta có x + 2 ≥ 0.
Û x ≥ –2.
Do đó tập A = [–2; +∞).
⦁ Ta có 5 – x ≥ 0.
Û x ≤ 5.
Do đó tập B = (–∞; 5].
Để xác định tập hợp A \ B, ta vẽ sơ đồ sau đây:
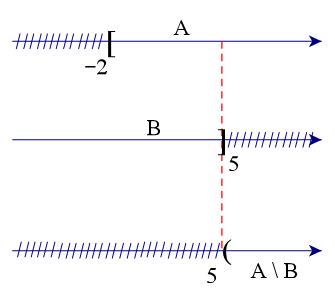
Từ sơ đồ, ta thấy A \ B = (5; +∞) (vì tập B có số 5 nên phần bù sẽ không lấy số 5).
Vậy ta chọn phương án C.
Câu 4. Cho hai tập khác rỗng A = (m – 1; 4], B = (–2; 2m + 2), m ∈ ℝ. Tìm m để A ∩ B ≠ ∅.
A. –1 < m < 5;
B. 1 < m < 5;
C. –2 < m < 5;
D. m > –3.
Đáp án: C
Giải thích:
Vì tập A khác rỗng nên ta có m – 1 < 4.
Û m < 5 (1)
Vì tập B khác rỗng nên ta có –2 < 2m + 2.
Û –4 < 2m.
Û m > –2 (2)
Từ (1) và (2), ta suy ra tập hợp A và B đều khác rỗng khi và chỉ khi –2 < m < 5 (*).
Để A ∩ B ≠ ∅ thì m – 1 < 2m + 2.
Nghĩa là, m > –3 (**).
Giao (*) và (**) lại với nhau, ta thu được kết quả –2 < m < 5.
Vậy ta chọn phương án C.
Câu 5. Một lớp học có 25 học sinh giỏi môn Toán, 23 học sinh giỏi môn Lý, 14 học sinh giỏi cả môn Toán và Lý và có 6 học sinh không giỏi môn nào cả. Hỏi lớp đó có bao nhiêu học sinh?
A. 54;
B. 40;
C. 26;
D. 68.
Đáp án: B
Giải thích:
Gọi T, L, K lần lượt là tập hợp các học sinh giỏi Toán, tập hợp các học sinh giỏi Lý và tập học các học sinh không giỏi môn nào cả.
Theo đề, ta có:
⦁ n(T) = 25;
⦁ n(L) = 23;
⦁ n(T ∩ L) = 14;
⦁ n(K) = 6.
Ta có sơ đồ Ven biểu diễn 3 tập hợp T, L, K như sau:
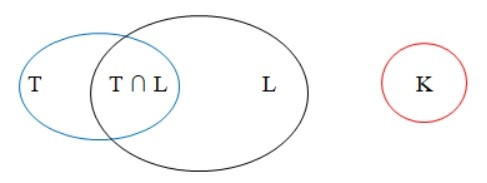
Khi đó số học sinh cả lớp là: n(T ∪ L) + n(K).
Ta có n(T ∪ L) = n(T) + n(L) – n(T ∩ L) = 25 + 23 – 14 = 34.
Vậy số học sinh cả lớp là: 34 + 6 = 40 (học sinh).
Do đó ta chọn phương án B.
Các câu hỏi trắc nghiệm Toán lớp 10 sách Chân trời sáng tạo có đáp án, chọn lọc khác:
Xem thêm các chương trình khác:
- Trắc nghiệm Toán lớp 10 có đáp án – Kết nối tri thức
- Trắc nghiệm Hóa học lớp 10 có đáp án – Kết nối tri thức
- Trắc nghiệm Địa Lí lớp 10 có đáp án – Kết nối tri thức
- Trắc nghiệm Công nghệ lớp 10 có đáp án – Kết nối tri thức
- Trắc nghiệm Giáo Dục Quốc Phòng lớp 10 có đáp án – Kết nối tri thức
- Trắc nghiệm Vật Lí lớp 10 có đáp án – Kết nối tri thức
- Trắc nghiệm Lịch sử lớp 10 có đáp án - Kết nối tri thức
- Trắc nghiệm Sinh học lớp 10 có đáp án – Kết nối tri thức
- Trắc nghiệm Tin học lớp 10 có đáp án - Kết nối tri thức
- Trắc nghiệm Kinh tế pháp luật lớp 10 có đáp án - Kết nối tri thức
- Trắc nghiệm Tiếng Anh lớp 10 có đáp án - Global Success Kết nối tri thức
- Trắc nghiệm Hóa học lớp 10 có đáp án – Cánh Diều
- Trắc nghiệm Vật Lí lớp 10 có đáp án – Cánh Diều
- Trắc nghiệm Địa Lí lớp 10 có đáp án – Cánh Diều
- Trắc nghiệm Công nghệ lớp 10 có đáp án – Cánh Diều
- Trắc nghiệm Giáo Dục Quốc Phòng lớp 10 có đáp án – Cánh Diều