TOP 20 câu Trắc nghiệm Ôn tập chương 8 (Chân trời sáng tạo 2024) có đáp án - Toán 10
Bộ 20 bài tập trắc nghiệm Toán lớp 10 Ôn tập chương 8 có đáp án đầy đủ các mức độ sách Chân trời sáng tạo giúp học sinh ôn luyện trắc nghiệm Toán 10 Bài tập cuối chương 8
Chỉ 150k mua trọn bộ Trắc nghiệm Toán lớp 10 Chân trời sáng tạo bản word (cả năm) có đáp án chi tiết:
B1: Gửi phí vào tài khoản 0711000255837 - NGUYEN THANH TUYEN - Ngân hàng Vietcombank (QR)
B2: Nhắn tin tới zalo Vietjack Official - nhấn vào đây để thông báo và nhận tài liệu.
Xem thử tài liệu tại đây: Link tài liệu
Trắc nghiệm Toán 10 Ôn tập chương 8 - Chân trời sáng tạo
I. Nhận biết
Câu 1. Giả sử một công việc có thể được thực hiện theo một trong ba phương án. Phương án A có 3 cách thực hiện, phương án B có 4 cách thực hiện, phương án C có 7 cách thực hiện (các cách thực hiện của cả ba phương án là khác nhau đôi một). Số cách thực hiện công việc đó là:
A. 14 cách;
B. 19 cách;
C. 84 cách;
D. 31 cách.
Đáp án: A
Giải thích:
Công việc có ba phương án thực hiện:
⦁ Phương án A có 3 cách thực hiện;
⦁ Phương án B có 4 cách thực hiện;
⦁ Phương án C có 7 cách thực hiện.
Ta thấy mỗi cách thực hiện của phương án này không trùng với bất kì cách nào của phương án kia. Do đó, theo quy tắc cộng, ta có 3 + 4 + 7 = 14 cách thực hiện công việc đã cho.
Vậy ta chọn phương án A.
Câu 2. Giả sử một công việc được chia thành ba công đoạn. Công đoạn A có 8 cách thực hiện; ứng với mỗi cách đó có 3 cách thực hiện công đoạn B; ứng với mỗi cách thực hiện công đoạn A và mỗi cách thực hiện công đoạn B có 6 cách thực hiện công đoạn C. Khi đó số cách thực hiện công việc đã cho là:
A. 17 cách;
B. 26 cách;
C. 30 cách;
D. 144 cách.
Đáp án: D
Giải thích:
Công việc được chia thành ba công đoạn:
⦁ Công đoạn A có 8 cách thực hiện;
⦁ Công đoạn B: ứng với mỗi cách thực hiện công đoạn A, có 3 cách thực hiện;
⦁ Công đoạn C: ứng với mỗi cách thực hiện công đoạn A và mỗi cách thực hiện công đoạn B, có 6 cách thực hiện.
Theo quy tắc nhân, ta có 8 . 3 . 6 = 144 cách thực hiện công việc đã cho.
Vậy ta chọn phương án D.
Câu 3. Cho tập hợp A có n phần tử (n ≥ 1) và số nguyên k (1 ≤ k ≤ n). Phát biểu nào sau đây sai?
A. Một chỉnh hợp chập k của n phần tử trên là mỗi cách lấy k phần tử của tập A và sắp xếp chúng theo một thứ tự;
B. Một hoán vị của tập A là mỗi cách sắp xếp n phần tử của tập A theo một thứ tự;
C. Một tổ hợp chập k của n phần tử là mỗi cách lấy k phần tử của A;
D. Mỗi hoán vị của n phần tử cũng chính là tổ hợp chập n của n phần tử đó.
Đáp án: D
Giải thích:
⦁ Mỗi cách sắp xếp n phần tử của tập A theo một thứ tự gọi là một hoán vị các phần tử đó. Do đó phương án B là phát biểu đúng.
⦁ Mỗi cách lấy k phần tử của A và sắp xếp chúng theo một thứ tự gọi là một chỉnh hợp chập k của n phần tử đó. Do đó phương án A là phát biểu đúng.
⦁ Mỗi tập con gồm k phần tử của A được gọi là một tổ hợp chập k của n phần tử. Do đó phương án C là phát biểu đúng.
⦁ Mỗi hoán vị của n phần tử cũng chính là chỉnh hợp chập n của n phần tử đó. Do đó phương án D là phát biểu sai.
Vậy ta chọn phương án D.
Câu 4. Cho n ≥ 1, n ∈ ℤ và 1 ≤ k ≤ n. Phát biểu nào sau đây sai?
A. P0 = 1;
B. Pn=Cnn;
C. Ckn=Cn−kn
D. = Akn=k!.Ckn
Đáp án: B
Giải thích:
⦁ Ta quy ước: P0 = 0! = 1. Do đó phương án A đúng.
⦁ Ta có Ckn=Cn−kn, với 0 ≤ k ≤ n.
⦁ Ta có Pn=Ann. Do đó phương án B sai.
Do đó phương án C đúng.
⦁ Ta có k!.Ckn=k!.n!k!.(n−k)!=n!(n−k)!=Akn.
Do đó phương án D đúng.
Vậy ta chọn phương án B.
Câu 5. Cho tập hợp X gồm n phần tử (n ≥ 1) và số nguyên k (1 ≤ k ≤ n). Một chỉnh hợp chập k của n phần tử là:
A. Một kết quả bất kì của sự sắp xếp k phần tử bất kì của tập hợp X;
B. Một kết quả của việc lấy k phần tử từ n phần tử của tập X và sắp xếp chúng theo một thứ tự nào đó;
C. Một số được tính bởi công thức: n(n – 1)(n – 2)…(n – k + 1);
D. Một kết quả của việc lấy k phần tử từ n phần tử của tập X.
Đáp án: B
Giải thích:
Mỗi cách lấy k phần tử của tập X và sắp xếp chúng theo một thứ tự gọi là một chỉnh hợp chập k của n phần tử đó.
Vậy ta chọn phương án B.
Câu 6. Biểu thức C04.x4+C14.x3y+C24.x2y2+C34.xy3+C44.y4 bằng:
A. (x + y)4;
B. (x – y)4;
C. (x + y)5;
D. (x – y)5.
Đáp án: A
Giải thích:
Theo công thức nhị thức Newton, ta có:
C04.x4+C14.x3y+C24.x2y2+C34.xy3+C44.y4=(x+y)4.
Vậy ta chọn phương án A.
Câu 7. Tổng số mũ của a và b trong mỗi hạng tử khi khai triển biểu thức (m + 2n)5 bằng
A. 4;
B. 5;
C. 6;
D. 7.
Đáp án: B
Giải thích:
Ta có tổng số mũ của a, b trong mỗi hạng tử khi khai triển (a + b)n luôn bằng n.
Vậy tổng số mũ của a và b trong mỗi hạng tử khi khai triển biểu thức (a + b)5 bằng 5.
Câu 8. Số hạng tử trong khai triển (a + b)99 bằng
A. 97;
B. 98;
C. 99;
D. 100.
Đáp án: D
Giải thích:
Ta có trong khai triển (a + b)n có n + 1 hạng tử.
Vậy trong khai triển (a + b)99 có 100 hạng tử.
II. Thông hiểu
Câu 1. Từ các chữ số 1; 5; 6; 7; 9 có thể lập được bao nhiêu số tự nhiên có 4 chữ số?
A. 3 125;
B. 120;
C. 20;
D. 625.
Đáp án: D
Giải thích:
Gọi ¯abcd là số cần tìm.
Việc lập một số tự nhiên có 4 chữ số gồm 4 công đoạn:
Công đoạn 1: Chọn số ở vị trí a, có 5 cách chọn một chữ số từ các chữ số 1; 5; 6; 7; 9.
Công đoạn 2: Chọn số ở vị trí b, có 5 cách chọn một số từ các chữ số 1; 5; 6; 7; 9.
Công đoạn 3: Chọn số ở vị trí c, có 5 cách chọn một số từ các chữ số 1; 5; 6; 7; 9.
Công đoạn 4: Chọn số ở vị trí d, có 5 cách chọn một số từ các chữ số 1; 5; 6; 7; 9.
Theo quy tắc nhân, ta có tất cả 5.5.5.5= 54 = 625 cách lập một số tự nhiên có 4 chữ số.
Vậy ta chọn phương án D.
Câu 2. Trên bàn có 8 cây bút chì khác nhau, 6 cây bút bi khác nhau và 10 cuốn tập khác nhau. Một học sinh muốn chọn một đồ vật duy nhất (một cây bút chì hoặc một cây bút bi hoặc một cuốn tập) thì số cách chọn khác nhau là:
A. 24;
B. 480;
C. 48;
D. 60.
Đáp án: A
Giải thích:
Việc chọn một đồ vật duy nhất có ba phương án thực hiện:
Phương án 1: Chọn một cây bút chì, có 8 cách chọn.
Phương án 2: Chọn một cây bút bi, có 6 cách chọn.
Phương án 3: Chọn một cuốn tập, có 10 cách chọn.
Theo quy tắc cộng, ta có tất cả 8 + 6 + 10 = 24 cách chọn một đồ vật duy nhất.
Vậy ta chọn phương án A.
Câu 3. Hội đồng quản trị của công ty X gồm 10 người. Hỏi có bao nhiêu cách bầu ra ba người vào ba vị trí chủ tịch, phó chủ tịch và thư kí, biết khả năng mỗi người là như nhau.
A. 1 000;
B. 720;
C. 30;
D. 27.
Đáp án: B
Giải thích:
Cách 1:
Việc bầu ra ba người vào ba vị trí chủ tịch, phó chủ tịch và thư kí gồm ba công đoạn:
Công đoạn 1: Bầu một người làm chủ tịch, có 10 cách chọn.
Công đoạn 2: Ứng với mỗi cách bầu một người làm chủ tịch, có 9 cách bầu một người làm phó chủ tịch.
Công đoạn 3: Ứng với mỗi cách bầu một người làm chủ tịch và bầu một người làm phó chủ tịch, có 8 cách bầu một người làm thư kí.
Theo quy tắc nhân, ta có tất cả 10.9.8 = 720 cách bầu ra ba người vào ba vị trí chủ tịch, phó chủ tịch và thư kí.
Vậy ta chọn phương án B.
Cách 2:
Để bầu ra ba người vào ba vị trí chủ tịch, phó chủ tịch và thư kí trong 10 người là một chỉnh hợp chập 3 của 10, tức là có A310=720 cách bầu.
Vậy ta chọn phương án B.
Câu 4. Từ các chữ số 0; 1; 2; 3; 4; 5, có thể lập được bao nhiêu số lẻ gồm 4 chữ số khác nhau?
A. 154;
B. 145;
C. 144;
D. 155.
Đáp án: C
Giải thích:
Gọi ¯abcd là số cần tìm.
Vì số được lập là số lẻ nên vị trí d có 3 cách chọn một trong các số 1; 3; 5.
Ứng với mỗi cách chọn đó, có 4 cách chọn số ở vị trí a từ 4 chữ số khác 0 và khác số ở vị trí d đã cho.
Ứng với mỗi cách chọn đó, có 4 cách chọn số ở vị trí b từ 4 chữ số còn lại.
Ứng với mỗi cách chọn đó, có 3 cách chọn số ở vị trí c từ 3 chữ số còn lại.
Theo quy tắc nhân, ta có tất cả 3.4.4.3 = 144 cách lập một số thỏa mãn yêu cầu bài toán.
Vậy ta chọn phương án C.
Câu 5. Một mạng đường giao thông nối các tỉnh A, B, C, D, E, F và G như hình vẽ, trong đó chữ số được viết trên mỗi cạnh là số con đường có thể đi từ tỉnh này đến tỉnh kia, chẳng hạn chữ số 2 viết trên cạnh AB có nghĩa là có 2 con đường nối A và B,...
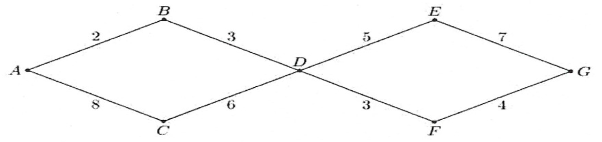
Số con đường từ A đến G là:
A. 101;
B. 2 538;
C. 38;
D. 1 462.
Đáp án: D
Giải thích:
Ta thấy để đi từ A đến G, ta bắt buộc phải đi qua D.
Bước 1: Đi từ A đến D.
• Phương án 1: Đi từ A, qua B, đến D thì có 2.3 = 6 con đường.
• Phương án 2: Đi từ A, qua C, đến D thì có 8.6 = 48 con đường.
Theo quy tắc cộng, ta có số cách đi từ A đến D là 6 + 48 = 54 con đường.
Bước 2: Đi từ D đến G.
• Phương án 1: Đi từ D, qua E, đến G thì có 5.7 = 35 con đường.
• Phương án 2: Đi từ D, qua F, đến G thì có 3.4 = 12 con đường.
Theo quy tắc cộng, ta có số cách đi từ D đến G là 35 + 12 = 47 con đường.
Vậy theo quy tắc nhân, ta có số cách đi từ A đến G là 54.47 = 2 538 con đường.
Do đó ta chọn phương án B.
Câu 6. Có ba môn thi Toán, Vật lí, Hóa học cần xếp vào 3 buổi thi, mỗi buổi một môn sao cho môn Toán không thi buổi đầu thì số cách xếp là:
A. 6;
B. 2;
C. 4;
D. 5.
Đáp án: C
Giải thích:
Việc xếp mỗi buổi một môn sao cho môn Toán không thi buổi đầu có hai phương án thực hiện:
Phương án 1: Môn Vật lí thi buổi đầu, thì số cách xếp hai môn còn lại vào 2 buổi còn lại là 2! cách xếp.
Phương án 2: Môn Hóa học thi buổi đầu, thì số cách xếp hai môn còn lại vào 2 buổi còn lại là 2! cách xếp.
Theo quy tắc cộng, ta có tất cả 2! + 2! = 2 + 2 = 4 cách xếp.
Vậy ta chọn phương án C.
Câu 7. Có bao nhiêu cách chọn và sắp xếp thứ tự 5 cầu thủ để đá luân lưu, biết rằng cả 11 cầu thủ đều có khả năng như nhau?
A. 55 440;
B. 20 680;
C. 32 456;
D. 41 380.
Đáp án: A
Giải thích:
Mỗi cách chọn và sắp xếp thứ tự 5 cầu thủ trong số 11 cầu thủ là một chỉnh hợp chập 5 của 11 phần tử.
Do đó số cách chọn và sắp xếp thứ tự 5 cầu thủ là: A511=55 440 cách chọn.
Vậy ta chọn phương án A.
Câu 8. Trong một bình đựng 4 viên bi đỏ và 3 viên bi xanh. Lấy ngẫu nhiên 2 viên bi. Có bao nhiêu cách lấy được 2 viên bi cùng màu?
A. 18;
B. 9;
C. 22;
D. 4.
Đáp án: D
Giải thích:
Việc lấy được 2 viên bi cùng màu có 2 phương án thực hiện:
Phương án 1: Lấy được 2 viên bi màu đỏ, có C24 cách chọn.
Phương án 2: Lấy được 2 viên bi màu xanh, có C23 cách chọn.
Do đó theo quy tắc cộng, ta có tất cả C24+C23=9 cách chọn.
Vậy ta chọn phương án B.
Câu 9. Trong một trường có 4 học sinh giỏi lớp 12, 3 học sinh giỏi lớp 11 và 5 học sinh giỏi lớp 10. Cần chọn 5 học sinh giỏi để tham gia một cuộc thi với các trường khác sao cho khối 12 có 3 em và mỗi khối 10, 11 có đúng 1 em. Vậy số tất cả các cách chọn là:
A. 60;
B. 180;
C. 330;
D. 90.
Đáp án: A
Giải thích:
Công việc chọn học sinh tham gia cuộc thi có 3 công đoạn:
Công đoạn 1: Chọn 3 học sinh giỏi lớp 12.
Mỗi cách chọn 3 học sinh giỏi trong số 4 học sinh giỏi lớp 12 là một tổ hợp chập 3 của 4 phần tử.
Do đó số cách chọn 3 học sinh lớp 12 là: C34 (cách).
Công đoạn 2: Chọn 1 học sinh giỏi lớp 11.
Mỗi cách chọn 1 học sinh giỏi trong số 3 học sinh giỏi lớp 11 là một tổ hợp chập 1 của 3 phần tử.
Do đó số cách chọn 1 học sinh lớp 11 là: C34 (cách).
Công đoạn 3: Chọn 1 học sinh giỏi lớp 10.
Mỗi cách chọn 1 học sinh giỏi trong số 5 học sinh giỏi lớp 10 là một tổ hợp chập 1 của 5 phần tử.
Do đó số cách chọn 1 học sinh lớp 10 là: C15 (cách).
Vậy theo quy tắc nhân, ta có tất cả C34.C13.C15=60 cách chọn 5 học sinh giỏi của trường đó.
Ta chọn phương án A.
Câu 10. Số hạng chứa x3y trong khai triển (xy+1y)5 là:
A. 3x3y;
B. 5x3y;
C. 10x3y;
D. 4x3y.
Đáp án: C
Giải thích:
Cách 1: Ta có:
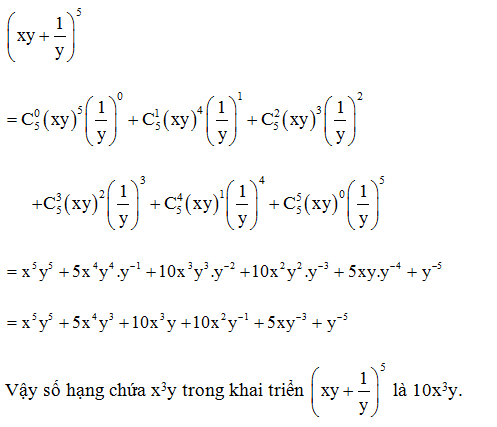
Cách 2:

Câu 11. Số hạng không chứa x trong khai triển P(x)=(x3−1x2)5 (x ≠ 0) (theo chiều số mũ của x giảm dần) là số hạng thứ:
A. 3;
B. 6;
C. 4;
D. 5.
Đáp án: C
Giải thích:
Theo nhị thức Newton, ta có:
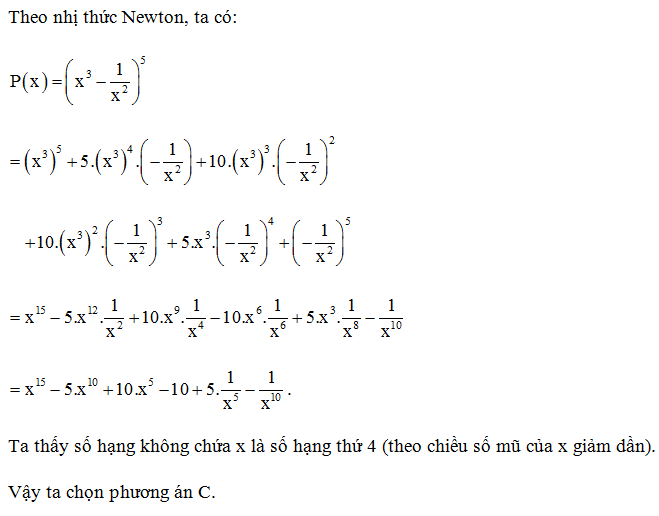
Câu 12. Cho x là số thực dương. Khai triển nhị thức (x2+1x)4, ta có hệ số của số hạng chứa xm bằng 6. Giá trị của m là:
A. m = 6;
B. m = 8;
C. m = 2;
D. m = 2 hoặc m = 6.
Đáp án: C
Giải thích:
Theo công thức nhị thức Newton, ta có:(x2+1x)4=(x2)4+4.(x2)3.1x+6.(x2)2.(1x)2+4.x2.(1x)3+(1x)4=x8+4.x6.1x+6.x4.1x2+4.x2.1x3+1x4=x8+4.x5+6.x2+4.1x+1x4
Ta thấy số hạng có hệ số bằng 6 là 6x2.
Suy ra m = 2.
Vậy ta chọn phương án C.
Câu 13. Giá trị của biểu thức (3+√2)4+(3−√2)4 bằng:
A. 193;
B. –386;
C. 772;
D. 386.
Đáp án: D
Giải thích:
Áp dụng công thức nhị thức Newton, ta có:
⦁ (3+√2)4=34+4.33.√2+6.32.(√2)2+4.3.(√2)3+(√2)4.
⦁ (3−√2)4=34+4.33.(−√2)+6.32.(−√2)2+4.3.(−√2)3+(−√2)4.
Suy ra (3+√2)4+(3−√2)4=2.[34+6.32.(√2)2+(√2)4]
= 2.(81 + 6.9.2 + 4) = 386.
Vậy ta chọn phương án D.
Câu 14. Biết rằng trong khai triển (x2+ax)5 (với x ≠ 0), hệ số của số hạng chứa 1x3 là 640. Khi đó giá trị của a bằng:
A. a = 4;
B. a = –4;
C. n ∈ {–4; 4};
D. a ∈ ∅.
Đáp án: C
Giải thích:
Cách 1: Ta có

Theo đề, ta có hệ số của số hạng chứa 1x3 là 640.
Tức là, 5a42=640.
⇔ 5a4 = 1 280
⇔ a4 = 256
⇔ a = 4 hoặc a = –4.
Vậy ta chọn phương án C.
Cách 2:
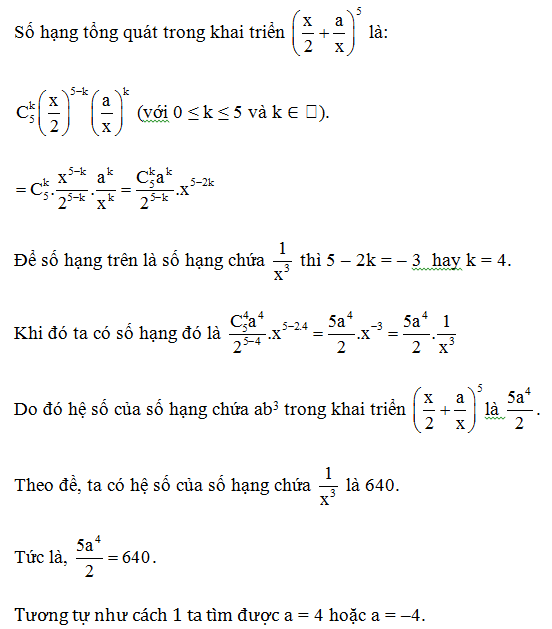
Vậy ta chọn phương án C.
Câu 15. Giá trị n nguyên dương thỏa mãn A2n−Cn−1n+1=5 là:
A. n = –2;
B. n = 5;
C. n ∈ {–2; 5};
D. n ∈ ∅.
Đáp án: D
Giải thích:
Ta có A2n−Cn−1n+1=5 (n ∈ ℤ, n ≥ 2)
⇔n!(n−2)!−(n+1)!(n−1)!(n+1−n+1)!=5
⇔n(n−1)(n−2)!(n−2)!−(n+1)n(n−1)!(n−1)!2!=5
⇔n(n−1)−(n+1)n2=5
⇔ 2n2 – 2n – n2 – n = 10
⇔ n2 – 3n – 10 = 0
⇔ n = 5 hoặc n = –2.
Vì n nguyên dương nên ta nhận n = 5.
Vậy ta chọn phương án D.
III. Vận dụng
Câu 1. Số 253 125 000 có bao nhiêu ước số tự nhiên?
A. 160;
B. 240;
C. 180;
D. 120.
Đáp án: C
Giải thích:
Ta có 253 125 000 = 23.34.58.
Do đó mỗi ước số tự nhiên của số 253 125 000 đều có dạng 2m.3n.5p, trong đó 0 ≤ m ≤ 3, 0 ≤ n ≤ 4, 0 ≤ p ≤ 8 và m, n, p ∈ ℕ.
Khi đó:
⦁ m có 4 cách chọn;
⦁ n có 5 cách chọn;
⦁ p có 9 cách chọn.
Theo quy tắc nhân, ta có tất cả 4.5.9 = 180 ước số tự nhiên.
Vậy ta chọn phương án C.
Câu 2. Cho tập hợp A = {0; 1; 2; 3; 4; 5; 6; 7}. Hỏi từ tập A có thể lập được bao nhiêu số tự nhiên gồm 5 chữ số đôi một khác nhau sao cho một trong 3 chữ số đầu tiên có chữ số 1?
A. 2 802;
B. 65;
C. 2 520;
D. 2 280.
Đáp án: D
Giải thích:
Gọi ¯abcde là số cần tìm.
Trường hợp 1: a = 1.
Khi đó b có 7 cách chọn, c có 6 cách chọn, d có 5 cách chọn và e có 4 cách chọn.
Do đó theo quy tắc nhân, ta có 7.6.5.4 = 840 số được lập.
Trường hợp 2: b = 1 hoặc c = 1 thì có 2 cách.
Khi đó a có 6 cách chọn (vì a ≠ 0 và a ≠ 1).
Ba vị trí còn lại lần lượt có 6, 5, 4 cách chọn.
Do đó theo quy tắc nhân, ta có 2.6.6.5.4 = 1 440 số được lập.
Vậy theo quy tắc cộng, ta có tất cả 840 + 1 440 = 2 280 số được lập.
Do đó ta chọn phương án D.
Câu 3. Từ các chữ số 0; 1; 2; 3; 4; 5, có thể lập được bao nhiêu số tự nhiên có 3 chữ số khác nhau và chia hết cho 9?
A. 16;
B. 18;
C. 20;
D. 14.
Đáp án: A
Giải thích:
Gọi ¯abc là số cần tìm, với a, b, c ∈ {0; 1; 2; 3; 4; 5}.
Vì ¯abc⋮9 nên tổng các chữ số a + b + c ⋮ 9.
Khi đó a; b; c là bộ số (0; 4; 5), (2; 3; 4) hoặc (1; 3; 5).
Trường hợp 1: a; b; c là bộ số (0; 4; 5).
Vị trí a có 2 cách chọn (số 4 hoặc số 5).
Vị trí b, c có 2! = 2 cách chọn từ 2 chữ số còn lại.
Do đó theo quy tắc nhân, ta có tất cả 2.2 = 4 số.
Trường hợp 2: a; b; c là bộ số (2; 3; 4) thì có 3! = 6 số.
Trường hợp 3: a; b; c là bộ số (1; 3; 5) thì có 3! = 6 số.
Vậy theo quy tắc cộng, ta có tất cả 4 + 6 + 6 = 16 số.
Ta chọn phương án A.
Câu 4. Một hội đồng gồm 5 nam và 4 nữ được bầu vào một ban quản trị gồm 4 người. Biết rằng ban quản trị có ít nhất một nam và một nữ. Số cách bầu chọn là:
A. 240;
B. 260;
C. 126;
D. 120.
Đáp án: D
Giải thích:
Việc bầu chọn một ban quản trị gồm 4 người có 3 phương án thực hiện:
Phương án 1: Chọn 1 nam và 3 nữ.
Chọn 1 nam trong số 5 nam, có C15 cách chọn.
Chọn 3 nữ trong số 4 nữ, có C34 cách chọn.
Do đó theo quy tắc nhân, số cách chọn 1 nam và 3 nữ là C15.C34 cách chọn.
Phương án 2: Chọn 2 nam và 2 nữ.
Chọn 2 nam trong số 5 nam, có C25 cách chọn.
Chọn 2 nữ trong số 4 nữ, có C24 cách chọn.
Do đó theo quy tắc nhân, số cách chọn 2 nam và 2 nữ là C25.C24 cách chọn.
Phương án 3: Chọn 3 nam và 1 nữ.
Chọn 3 nam trong số 5 nam, có C35 cách chọn.
Chọn 1 nữ trong số 4 nữ, có C14 cách chọn.
Do đó theo quy tắc nhân, số cách chọn 3 nam và 1 nữ là C35.C14 cách chọn.
Vậy theo quy tắc cộng, ta có tất cả C15.C34+C25.C24+C35.C14=120 cách chọn.
Ta chọn phương án D.
Câu 5. Tổng S=C05+3C15+32C25+33C35+34C45+35C55 bằng:
A. S = 35;
B. S = 25;
C. S = 3.25;
D. S = 45.
Đáp án: D
Giải thích:
Theo công thức nhị thức Newton, ta có:

Câu 6. Hệ số của số hạng x10 trong khai triển (1 + x + x2 + x3)5 là:
A. 5;
B. 50;
C. 101;
D. 105.
Đáp án: C
Giải thích:
Ta có (1 + x + x2 + x3)5 = [1 + x + x2(1 + x)]5
= [(1 + x)(1 + x2)]5 = (1 + x)5.(1 + x2)5.
Theo công thức nhị thức Newton, ta có:
⦁ A = (1 + x)5
= 15 + 5.14.x + 10.13.x2 + 10.12.x3 + 5.1.x4 + x5
= 1 + 5x + 10x2 + 10x3 + 5x4 + x5.
⦁ B = (1 + x2)5
= 15 + 5.14.x2 + 10.13.(x2)2 + 10.12.(x2)3 + 5.1.(x2)4 + (x2)5
= 1 + 5x2 + 10x4 + 10x6 + 5x8 + x10.
Suy ra (1 + x + x2 + x3)5 = A.B
Khi đó ta có số hạng chứa x10 trong khai triển (1 + x + x2 + x3)5 là:
xi.xj = x10 hay xi + j = x10 với xi là lũy thừa của số hạng trong A, xj là lũy thừa của số hạng trong B (i ∈ {0; 1; 2; 3; 4; 5} và j ∈ {0; 2; 4; 6; 8; 10}).
Do đó ta có bảng sau:
|
j |
i |
|
10 |
0 |
|
8 |
2 |
|
6 |
4 |
Từ bảng ta có số hạng chứa x10 trong khai triển là:
1.x10 + 10x2.5x8 + 5x4.10x6
= x10 + 50x10 + 50x10 = 101x10.
Vậy hệ số của số hạng chứa x10 trong khai triển (1 + x + x2 + x3)5 là 101.
Do đó ta chọn phương án C.
Câu 7. Có bao nhiêu số tự nhiên n thỏa mãn 14.P3.Cn−3n−1<A4n+1?
A. 1;
B. 2;
C. 3;
D. Vô số.
Đáp án: D
Giải thích:
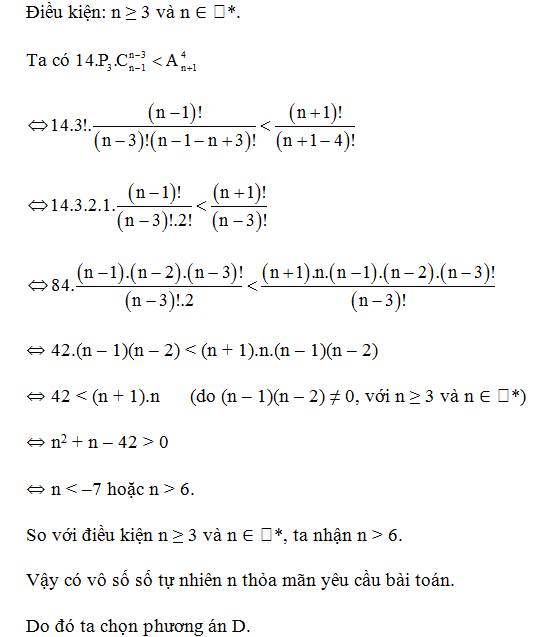
Các câu hỏi trắc nghiệm Toán lớp 10 sách Chân trời sáng tạo có đáp án, chọn lọc khác:
Xem thêm các chương trình khác:
- Trắc nghiệm Toán lớp 10 có đáp án – Kết nối tri thức
- Trắc nghiệm Hóa học lớp 10 có đáp án – Kết nối tri thức
- Trắc nghiệm Địa Lí lớp 10 có đáp án – Kết nối tri thức
- Trắc nghiệm Công nghệ lớp 10 có đáp án – Kết nối tri thức
- Trắc nghiệm Giáo Dục Quốc Phòng lớp 10 có đáp án – Kết nối tri thức
- Trắc nghiệm Vật Lí lớp 10 có đáp án – Kết nối tri thức
- Trắc nghiệm Lịch sử lớp 10 có đáp án - Kết nối tri thức
- Trắc nghiệm Sinh học lớp 10 có đáp án – Kết nối tri thức
- Trắc nghiệm Tin học lớp 10 có đáp án - Kết nối tri thức
- Trắc nghiệm Kinh tế pháp luật lớp 10 có đáp án - Kết nối tri thức
- Trắc nghiệm Tiếng Anh lớp 10 có đáp án - Global Success Kết nối tri thức
- Trắc nghiệm Hóa học lớp 10 có đáp án – Cánh Diều
- Trắc nghiệm Vật Lí lớp 10 có đáp án – Cánh Diều
- Trắc nghiệm Địa Lí lớp 10 có đáp án – Cánh Diều
- Trắc nghiệm Công nghệ lớp 10 có đáp án – Cánh Diều
- Trắc nghiệm Giáo Dục Quốc Phòng lớp 10 có đáp án – Cánh Diều
